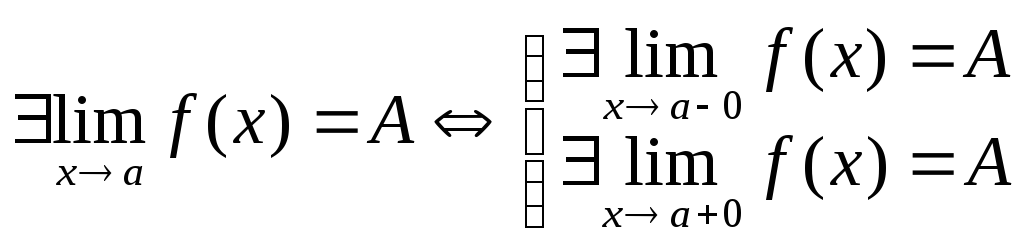Лекции Логинова [1-2 курс, МИФИ] / МАТАН 1 сем / matan_2

2. Предел последовательности

{x_n} сходится (у нее есть конечный предел)

{x_n} расходится. Построить отрицание.

Геометрическое определение предела

Интервал (a-,a+) называется - окрестностью точки a.

Опр. Вне любой окрестности точки a содержится конечное число членов последовательности.

Замечание.

Бесконечно малая последовательность {x_n}:.

Замечание. {x_n}a x_n=a+_n,_n- бесконечно малая.

3. Несобственные пределы

Последовательность, удовлетворяющая одному из этих условий называется бесконечно большой б.б.

Замечание. Бесконечно большая последовательность расходится.

Геометрическое определение предела

Окрестность несобственных точек -, +, .

Окрестностью - называется множество вида (-,b) для любого b.

Окрестностью + называется множество вида (b,+) для любого b.

Окрестностью  называется множество вида (-,-b) (b,+) для любого b. Отметим, что при отрицательных b это множество всех вещественных чисел.

Геометрическое определение предела. Число или символ a называется пределом последовательности {x_n}, если вне любой окрестности имеется лишь конечное число членов этой последовательности.

§2. Теоремы о пределах последовательностей

1.Простейшие свойства сходящихся последовательностей

Выбрасывание или добавление конечного числа членов не нарушает сходимости последовательности и величины ее предела.

Т1. Сходящаяся последовательность имеет единственный предел

Т2. Сходящаяся последовательность ограничена.

Доказательство: . Возьмем =1 по определению предела для него Nn>N:a-1<x_n<a+1. В таком случае для числа b=max{|x₁|,…,|x_N|,|a-1|,|a+1|} будет выполнено n:|x_n|<b.

Т3. (О трех последовательностях)

Т4.

Следствие 1.

Следствие 2.

Замечание.

2. Монотонные последовательности

Т5. Всякая ограниченная сверху, монотонно возрастающая последовательность {x_n} имеет конечный предел .

Замечание 1. Аналогично доказывается, что всякая ограниченная снизу монотонно убывающая последовательность сходится.

Лекция 5

Замечание 2. Если {[a_n,b_n]} система вложенных стягивающихся к нулю отрезков и с[a_n,b_n], то .

Доказательство:

Пример. Число e

Индукцией по n доказывается формула ( Бином Ньютона ):

.

Для последовательности x_n=(1+1/n)ⁿ получим

При переходе от n к n+1 каждое слагаемое в этой сумме увеличивается и растет их общее число, поэтому x_n<x_n+1. Каждая скобка <1 и , поэтому

. Монотонно возрастающая ограниченная последовательность сходится к некоторому числе, которое обозначается e. Это трансцендентное число называется числом Эйлера e=2.7182818284…

§3. Некоторые свойства последовательностей связанные со свойством непрерывности вещественных чисел

1.Подпоследовательность. Теорема Больцано-Вейерштрасса

Опр. Дана последовательность {x_n} и последовательность натуральных чисел {n_k},1n₁<n₂<…<n_k<n_k+1<…

тогда последовательность {y_k}, называется подпоследовательностью последовательсти {x_n}.

Пример: sin n, sin 2n.

Замечание. Отметим, что n_kk.

Теорема 1. Если (a - число или символ) , то для любой ее подпоследовательности {y_k}, ,будет .

Доказательство: Вне любой окрестности a содержится лишь конечное число членов {x_n}, следовательно и конечное число {y_k}.

Теорема 2. (Больцано, Вейерштрасс) Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.

Доказательство. Пусть [a,b]{x_n}.

Разделим отрезок [a,b] пополам, обозначим [a₁,b₁] тот из полученных двух отрезков, который содержит бесконечно много членов последовательности {x_n}. Возьмем какой-нибудь член последовательности, лежащий в [a₁,b₁], его индекс обозначим n_1.

Разделим отрезок [a₁,b₁] пополам, обозначим [a₂,b₂] тот из полученных двух отрезков, который содержит бесконечно много членов последовательности {x_n}. Возьмем какой-нибудь член последовательности, лежащий в [a₂,b₂] и имеющий индекс больший, чем n₁, его индекс обозначим n_2. Продолжая этот процесс, мы построим подпоследовательность . Система отрезков [a_k,b_k] представляет собой систему вложенных, стягивающихся к нулю отрезков ( b_k-a_k=(b-a)/2^k). Общую точку обозначим c. Так как c[a_k,b_k], то . Откуда следует, что (Следствие 2 из Теоремы 4 §2).

Определение. Предел подпоследовательaности называется частичным пределом (в том числе )

Замечание 1. Частичных пределов у последовательности может быть много.

Пример: Последовательность всех рациональных чисел {r_n} имеет своим частичным пределом любое вещественное число.

Замечание 2. Для того, чтобы a (число или символ) было частиным пределом последовательности {x_n} н. и д., чтобы любая окрестность a содержала бесконечно много членов последовательности {x_n}.

Следствие. Если некоторая окрестность a содержит конечное число членов последовательности, то a не является частичным пределом.

Замечание 3. У любой последовательности существует хотя бы один частичный предел (конечный или бесконечный)

Доказательство: Рассмотреть два случая: Ограниченая последовательность (Теорема Больцано-Вейерштрасса), неограниченая последовательность.

2.Верхний и нижний пределы последовательности

Определение. (Наибольший частичная предел последовательности {x_n} называется ее верхним пределом, , где X – множество всех частичных пределов. Аналогично .

Лекция 6

Замечание. Если , (число или символ), то

Теорема. У любой последовательности существует как верхний, так и нижний пределы. (без доказательства)

1) Если последовательность неограничена сверху, то

2) Ограничена сверху. A- множество частичных пределов

.

Осталось показать, что b есть частичный предел. Действительно, в любой окрестности b есть хотя бы один частичный предел, следовательно бесконечно много членов {x_n}.

3. Фундаментальная последовательность. Критерий Коши

Условие Коши:>0Nn>Np:|x_n+p-x_n|<

Определение. Фундаментальная последовательность – последовательность, удовлетворяющая условию Коши.

Т. (Критерий Коши). Для того, чтобы последовательность {x_n} сходилась Н. и Д., чтобы она была фундаментальна.

Доказательство: Необходимость.

Достаточность. >0. Для =/2N₁n>N₁:|x_n+p - x_n|</2(*)

Таким образом, все члены последовательности начиная с некоторого оказались в окрестности числа x_n (зафиксировать некоторое n>N₁), следовательно последовательность ограничена. По теореме Больцано-Вейерштрасса существует подпоследовательность . Для ранее выбранного  . В качестве такого K следует взять некоторое K, удовлетворяющее условию n_K>N₁. В этом случае согласно (*) число N=n_k будет удовлетворять условию

n>N: |x_n-a|<|x_n-x_N+x_N-a|</2+/2=, ч.т.д..

§4. Свойства последовательностей

1.Операции над последовательностями. Свойства пределов, связанные с операциями

Определения операций. Сумма двух последовательностей, умножение на число.

1) {_n} б.м.  |_n| б.м.

2) {_n+_n} б.м.

Следствие. {_n+_n+…+_n} б.м.

3) б.м. на ограниченную является б.м.

Следствие. Произведение конечного числа б. м.

4) {1/_n} б.б., если {_n} б.м. _n0

{1/_n} б.м., если {_n} б.б., _n0

5)Ранее отмечалось

,{_n} б.м.

6) {x_n},{y_n} сходятся, то сходится {x_n+y_n} и

Следствие. Конечная сумма.

Замечание. Нарушается, если хотя бы один из пределов 

7) {x_n},{y_n} сходятся, то сходится {x_ny_n} и

Следствие 1.Если {x_n} сходятся, то сходится {сx_n} и

Следствие 2. x_na

8) x_na|x_n||a|

9) x_na, y_nb, y_n0, b0

Лемма. Если y_nb, y_n0, b0, то |1/y_n| ограничена.

Доказательство:

Доказательство свойства 9)

1/(by_n) по лемме ограничена.

Глава 3. Предел функции. Непрерывность

§1. Основные понятия, относящиеся к функции

1. Определение функции. Обратная функция. Суперпозиция

область значений. Если различным x отвечают различные y , то yY!xX:f(x)=y

такая функция называется обратной и обозначается f^-1.

Т. Если f(x) строго монотонна на X и имеет область значений Y, то на Y существует f^-1.

Суперпозиция g:TX,f:XY,fg:TY

2.Ограниченность. Точные грани

f определена на X

Ограничена на множестве X. bxX:|f(x)|b

Ограничена сверху на множестве X. bxX:f(x)b

Ограничена снизу на множестве.

Точная верхняя грань

1.xX:f(x)b

2.>0xX:f(x)>b-

Формулировка Верхняя грань достигается

Лекция 7

3.Елементарные функции

Функции

y=c, y=x^a, y=a^x, y=log_ax (x>0)

Тригонометрические и их обратные называются основными элементарными функциями.

Всякая функция, полученная применением конечного числа арифметических операций и суперпозиций над основными элементарными функциями называется элементарной функцией.

Примеры: Многочлен, дробно рациональная функция

§2. Предел функции

1.Определение предела по Коши

Пусть f(x) определена на (a,b) за исключением быть может точки x₀(a,b). Обозначим область определения этой функции X.

если >0>0x,0<|x-x₀|<,xX:|f(x)-A|<

Геометрическое определение: Проколотая окрестность =(a-,a+)\{a}, a-число или символ.

a-число U(a)=(a-,a+),

a=+, U(a)=(b,+),

a=-, U(a)=(-,b),

a=, U(a)=(-,b)(b,)

Прмер: ,

2. Предел слева, предел справа , a – число.

f(x) определена и (c,a)

Аналогично определяется .

Замечание.

7