
Шпоры по матану [3 семестр] / тест-теория
.docx1. установить соответствие если z=x+iy, то Re z=x ; Im z=y
1. установить соответствие i2=-1;i5=i
1.модуль
комплексного числа z=x+iy
равен

1.число z=x+iy называется комплексным, если x,y –
действительные числа, in=-1, a n=2
1.если число z=x+iy, то -z=-x-iy
1.установить
соответствие если Re
и Im
представлены через z
и z
Re
z=
(z
+ z)/2;
Im
z=
(z
- z)/2i
1.если
z=x+iy
, то сопряженное число z
равно x-iy
1.два
комплексных числа z=x+iy
и w=u+iv
равны
 , когда x=u
и y=v
, когда x=u
и y=v
1.если
z=x+iy,
x>0,
то arg
z=arctg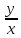
1.установить соответствие z+w=(x+u)+i(y+v); z-w=(x-u)+i(y-v); zw= (xu-yv)+i(xv+yu)
2.логарифмическая функция Ln z от комплексной переменной z=x+iy равна ln |z|+i arg z
2.если
arg z =φ,
то
arg z=-φ
2.установить
соответствие
[x=0, y>0] arg z=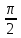 ;
[x<0, y<0] arg z= arctg
;
[x<0, y<0] arg z= arctg ;
[x<0,y≥0] arg z=π+
arctg
;
[x<0,y≥0] arg z=π+
arctg
2.если lim z>0, arg z=a, то arg(-z)=-π+a
2.установить
соответствие |z|= ;
|z|2=z
;
|z|2=zz
2.если
arg
z
=φ,
то Arg
zn
(n
c
N)
равен nφ
+2πk
2.установить соответствие для чисел z≠0, w≠0 Arg zw=Arg z+Arg w; Argz/w=Arg z-Arg w
2.если z=x+iy, то ln z равен ln|z|+i arg z
2.установить
соответствие zw=z/w
; z/w=
z
w
?
2.если Im z<0, arg z=a, то arg(-z)=π+a
3.если r=|z|, φ=arg z, то z=r(cosφ+i sinφ)
3.формула Эйлера имеет вид eiφ= cosφ+i sinφ
3.если z=r(cosφ+i sinφ), то сопряженное число
z=r(cosφ-i
sinφ)
3.если
z=r(cosφ+i
sinφ),
то
число
zn
(ncN)
равно
rn(cos nφ+i sin nφ)
3.установить соответствие eiφ= cosφ+i sinφ
3.установить соответствие sh z=(ez-e-z)/2; sin z=(eiz-e-iz)/2
3.если
z=r(cosφ+i
sinφ),
то
 (n
(ncN)
равен
 (cos
(cos
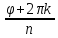 + isin
+ isin )
, k=0,1,…,n-1. ?
)
, k=0,1,…,n-1. ?
3.установить соответствие cos z=(eiz+e-iz)/2; ch z=(ez+e-z)/2
3.если
z=r
eiφ,
w=ρ
eiφ,
то частное
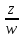 равно
равно
 ei(φ-ψ)
ei(φ-ψ)
3. если z=r eiφ, w=ρ eiφ, то произведение zw равно rρei(φ+ψ)
4.функция φ(x,y) называется гармонической в области G,
если она имеет непрерывные частные производные первого
и
второго порядка и удовлетворяет
уравнению
 +
+ =0
=0
4.функция f(z) диф в точке z , если сущ производная f’(z),
которая
равна
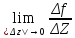
4.функция f(x,y)=u(x,y)+iv(x,y) удовлетворяет условиям
Коши-Римана,
если
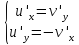
4.если
zn=xn+iyn,
n=1,2,3,…,
z0=x0+iy0,
то утверждение
 =z0
(zn
=z0
(zn
равносильно
(эквивалентно) |zn-z0|
4.Условия Коши-Римана являются критерием того, что функция
f(x,y)=u(x,y)+iv(x,y) ?
4.аналитичность функции f(z) в области D означает, что она дифференцируема
в каждой точке области D
4.точка z=z0 является нулем k-го порядка функции f(z) тогда и только тогда,
когда в некоторой
окрестности
этой точки функция
 аналитическая и не равна 0
аналитическая и не равна 0
4.особой точкой функции f(z) называется точка, в которой f(z) не аналитическая
4.функция f(x,y)=u(x,y)+iv(x,y) – однозначно определена и непрерывна в области G,
Г
– кусочно-гладкая кривая в области G,
тогда
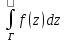 равен
равен

4.если функция f(z) аналитична в некоторой окрестности точки
z0, а в самой точке z0 не аналитична, то
точка z0 называется изолированной особой точкой
5.уст.соот.
ln(1+z)=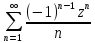 ;
cos
z=
;
cos
z=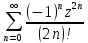
5.если
ряд
 cходится
в точке z=z0
, то этот ряд сходится во всех
cходится
в точке z=z0
, то этот ряд сходится во всех
точках |z|<|z0|
5.уст
соответ: 1) 1-z+z2-…+(-1)nzn+…=1/(1+z);
2) z+ +…+
+…+ +…=-ln(1-z)
+…=-ln(1-z)
5.по теореме Коши, если функция F(z) – аналитическая в односвязной
области D и Г – кусочно-гладкий
замкнутый контур,
принадлежащий D,
то интеграл
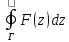 =0
=0
5. если функция f(z) – аналитическая в односвязной замкнутой области
G
с кусочно-гладкой границей Г и
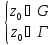 то интеграл
то интеграл

 равен
f(z0)
равен
f(z0)
5.если
ряд
 расходится
в точке z=z1,
то этот ряд расходится
расходится
в точке z=z1,
то этот ряд расходится
во всех точках z, таких что |z|>|z1|
5.уст
соот:1) 1+z+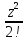 +…+
+…+ +…=ez;
2) z-
+…=ez;
2) z-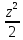 +
+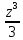 -…+
-…+ +…=ln(1+z)
+…=ln(1+z)
5. если функция f(z) – аналитическая в односвязной замкнутой области G
с
кусочно-гладкой границей С и z0 G,
то интеграл
G,
то интеграл

 =f’(z0)
=f’(z0)
5.
1) =
=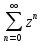 ;
2) ez=
;
2) ez=
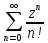 ;
;
5.если
функция f(z)
– аналитическая в замкнутом кольце G:
r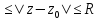 (r≤R),
(r≤R),
то
коэффициенты Cn
(n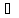 Z)
ряда Лорана в G
имеют вид:
Z)
ряда Лорана в G
имеют вид:

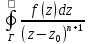 , где
, где
Г - кусочно-гладкая граница
6.уст
соот: 1) простой полюс: –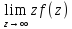 ;
2)существенно особую точку:
;
2)существенно особую точку:
коэф при z-1 со знаком минус в разложении f(z) в ряд Лорана
6.уст
соот: 1) устранимая особая точка
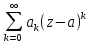 ;
2)
;
2)
полюс
порядка m
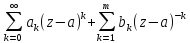
6.точка
z= является устранимой особенностью
функции f(z),
если в
является устранимой особенностью
функции f(z),
если в
ряде
Лорана этой функции в окрестности z=
равны нулю коэффициенты c-k (k=1,2,…)
6.
1)существенно особая точка
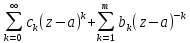 ;
2)
;
2)
простой полюс
 +
+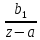
6.точка
z=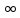 есть
полюс порядка k
функции f(z),
если ряд Лорана этой функции в окрестности
точки z=
есть
полюс порядка k
функции f(z),
если ряд Лорана этой функции в окрестности
точки z=
имеет
вид:
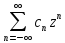
6.если
функция f(z)
– аналитическая в проколотой окрестности
точки а: 0<|z-a|< и
и
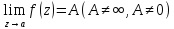 , то
, то
точка называется устранимой особой точкой
6.уст соот: 1) аналитическая 2)имеет полюс порядка 3)имеет простой полюс
