Эргодическая теорема для цепей Маркова

] известно (???) 

a) выполняется это уравнение

б) Всегда выполняется 1 или 2:

1. все j=0

2. j=1

3. у цепи имеется единственное стационарное распределение  тогда существует положительный y не единственный возвратный класс состояний(p_j)

Доказательство

-вектор

означает что p=p т.е. (I-p)=0 – условие для стационарного распределения

j-стационарное распределение т.е. цепь стремится к своему старшему распределению.

Если какое-то является опис. Распределением м/у (то легко показать q_j^(m)j при n) т.к. q_j⁽ⁿ⁾=_ q_p_j⁽ⁿ⁾j_ q_=j)

то различные  отрезка времени от 0 до N – (достаточно большой) т.е. до выхода на стационарный режим.

Лемма Фату:

] существуют положительные числа

- ряд сходится

рассмотрим нижний предел

а) (1) по лемме Фату

(1) ур. Ч.К.

Следовательно

Хотим доказать равенство  что меньше не может быть

] При j₀ <  возьмем и сложим эти неравенства по всем j  это <

поменяем порядок суммирования i и j местами

одно и тоже

Получили противоречие

Следовательно имеет место равенство.

б) j=по уравнению из а) p=

pⁿ=

следовательно

для любого j j(1-_I)=0

] существует м/у X_n и есть подмножество X_nk, n₁<n_{2 …} <n_k

X_nk – ж/у (но она не однородная)

Напишем X_t, где tR⁺  (0,)

И этот процесс можно было бы считать м/у.

Он является: м/у с непрерывным временем, если при любом выборе t₁…t_k…последовательность X_+k – это м/у. И будем считать что она однородная м/у, если X_t*k является однородным м/у для всякого t (сколь угодно маленького) Установим соответствие между м/у (с непрерывным вектором и нет).

Вектор ??? Q=(q₁,q₂,…) можно p_in(t)=для всех интервалов времени длинны t задать.

Переходим E_n-1, E_n+1, E_n.

Матрица перех. Вероятностей за 1 шаг у нас нет т.к. t – мало. Можно определить p(k)

P_ij(t)=p(X_t+=j/X_=i) (p^k у нас нет)

<t+ Условная вероятность составляет E_ в момент t+ при условии что в момент  это сост. E_I

т.к. мы не можем возводить матрицу в нецелую степень)

(зависит от продолжения t)

Уравнение Ч.К. выполняется

(ничего не можем сказать) и

тоже будет выполнятся как

Конечномерное распред. Мн. Можно определить м/у (не однородная)

P(x_t1=i₁,X₂=i₂,…,X_tk=i_k)=p_ik-1,i_k(t_k-1,t_k)*p_ik-2,ik-1*(t_k-2,t_k-1)_…p_i0i1(t₀,t₁)q+0 p_ij(t) – могут менятся со временем  указ.  конца пром. времени.

м/у с непр. вр. однозначно определяется вектором начального распределения и набором матриц

p(t)=(p_ij(t))

но p(t+)=p(t)*p() – обладают этим свойством t,>0 

эти матрицы над полугруппами (если обладают такими св-ми)

p(0)=E

i=j  p_ii(0)=1

i<>j  p_ij(0)=0

? – как определить эту полугруппу матриц? Как найти p_ij(t)? Какую хар-ку выбрать через которую эта подгруппа определится?

Достаточно знать полугруппу на маленьком промежутке времени и  знаем всю гр. P_n(t)=p{Z(t)=n}

Действительно t=nt₀+t₁, t₁<t₀

P(t)=p(nt₀)*p(t₁)=p(t₀)*p(t₁)  Нужно знать значение p(t) близких к нулю  будем знать хар-ку Маркова инфинитизимальная х-ка

] p(t) – диф-ал в нуле, т.е. p_ij(t) в точке 0

Покажем, что она будет диф-ма и в любой другой точке

(p(t+t)-p(t))/t=(p(t)p(t)-p(t))/t=(p(t)(p(t)-E))/t=p(t)(p(t)-p(0))/tp(t)p’(0) при t0

p’(0) – диф-л в нуле значит, что: если ф-я дифф. p_ii(е)=(значит в нуле)1+_iit+0(t)

1 – диагональный элемент матрицы

i<>j p_ij(t)=_ij=0

Выведем диф-ое ур-ие с помощью которого p_ij можно находить

Введём матр. Производную

=(_ij) – сумма эл-ов по строкам = 0

Теорема: В этих условиях имеет место системы уравнений – системы Колмогорова

1. Обратная систему уравнений Колмогорова

p_ij’(t)=

2. Прямая СУ Колмогорова

p_ij’=

Начальные условия

Эти системы при i<>j решаются однозначно  имеется  момент однозначно востановить p(t)

Доказательство:

перейдем к пределу

- обратное уравнение системы Колмогорова

2-й способ представления

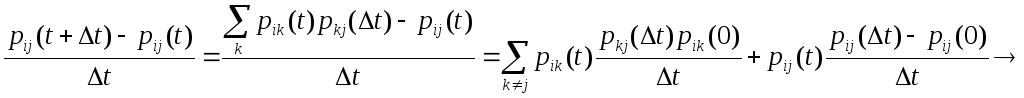
- прямая СУ Колмогорова / Что и требовалось доказать

Q и  - определяют м/у однозначно (остальные формулы для дискретных цепей используются для м/у непрер. врем.)

Пример:

Расс. произв, р. со временем возрастает т.е. X_t имеет возрастающую траекторию т.е. p_ij(t)=0, если j<i 

] _ij= задаём матрицу 

Возьмём СУ Колмогорова

Обратная СУК:

(2) (*)

(<>0, j=I, j=I+1  2 слагаемых)

(*) = -p_ij(t)+p_i+1,j i<>j

(Есть один особый случай когда i=j)

1. p_ij’(t)=-p_ii(t)

pi+1,j не будет т.к. j>=ш, а так от i+1 до I (а н ас ??? возрастает)

Решим эти уравнения

(1) ln p_ii(t)=-t+C p_ii(t)=e^-t+C₁ t=0C₁=1

p_ii(t)=e^-t

2. f_i,i+1(t)=e^tp_i,i+j(t)  f_i,i+1^’(t)=e^t(p_i,i+j(t)+p_i,i+j^’(t))=f_i+1,i+j(t)

Сист ема диф ур для f

f_i,i+j^’(t)=f_i+1,i+j(t)

f_ii(t)=f₀₀(t)=1

Получили f_i,i+1’(t)

(чтобы доказать по ММИ некую формулу, для того чтбы найти формулу рассмотрим частный случай)

f_i,i+1’=f_i+1,i+1(t)=

f_i,i+1(t)=t+C

p_i,i+1(0)=0 |  t=0

f_i,i+1(0)=0 |

f_i,i+1(t)=t