6. Загальна економіко-математична модель задачі лінійного програмування

Загальна лінійна економіко-математична модель економічних процесів та явищ — так звана загальна задача лінійного програмування подається у вигляді:

(2.1)

за умов: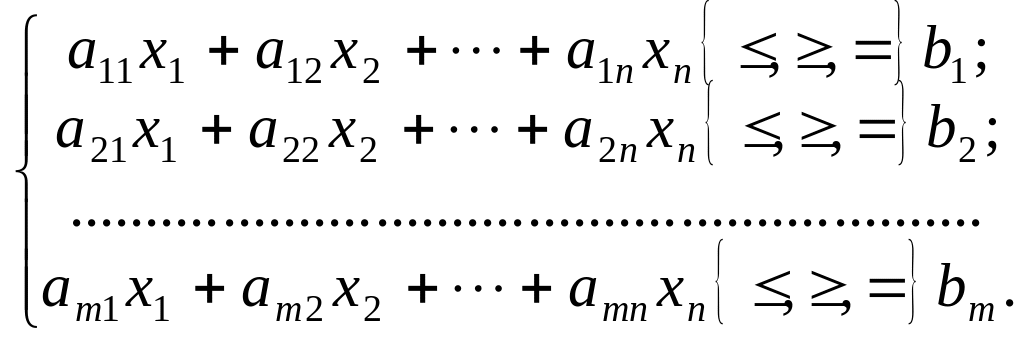 (2.2)

Отже, потрібно знайти значення змінних x₁, x₂, …, x_n, які задовольняють умови і цільова функція (2.1) набуває екстремального (максимального чи мінімального) значення.

Вектор Х = (х₁, х₂, …, х_n), координати якого задовольняють систему обмежень (2.2) та умови невід’ємності змінних (2.3), називається допустимим розв’язком (планом) задачі лінійного програмування. Допустимий план Х = (х₁, х₂, …, х_n) називається опорним планом задачі лінійного програмування

Опорний план Х = (х₁, х₂, …, х_n), називається невиродженим, якщо він містить точно m додатних змінних, інакше він вироджений.

Опорний план , за якого цільова функція досягає масимального (чи мінімального) значення, називається оптимальним розв’язком (планом) задачі лінійного програмування.

Задачу (2.1)—(2.3) можна легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (2.2) всі b_i (i = 1, 2, …, m) невід’ємні, а всі обмеження є рівностями.

Якщо якесь b_i від’ємне, то, помноживши i-те обмеження на (– 1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності а_i1х₁ + а_i2х₂ + … + а_inx_n ≤ b_i, то останню завжди можна звести до рівності, увівши додаткову змінну x_{n + 1}: a_i1x₁ + a_i2x₂ + … + + a_in x_n + x_{n + 1} = b_i.

Аналогічно обмеження виду а_k1x₁ + a_k2x₂ + … + a_knx_n ≥ b_k зводять до рівності, віднімаючи від лівої частини додаткову змінну х_n + 2, тобто: a_k1x₁ + a_k2x₂ + … + a_knx_n – x_{n + 2} = b_k (х_n+1 ≥ 0, х_n+2 ≥ 0).

Доведемо, що заміна нерівностей рівняннями за допомогою введення додаткових змінних не змінить розв’язку початкової задачі. Розглянемо лінійну нерівність з n невідомими:

Для зведення нерівності (2.4) до рівняння необхідно до її лівої частини додати деяку невід’ємну величину х_{n + 1} ≥ 0. У результаті дістаємо лінійне рівняння, яке містить n+1 змінну:

a₁x₁ + a₂x₂ + … + a_nx_n + x_{n + 1} = b. (2.5)

7. Форми запису задач лінійного програмування

Задачу лінійного програмування зручно записувати за допомогою знака суми «». Справді, задачу (2.1)—(2.3) можна подати так:

за умов: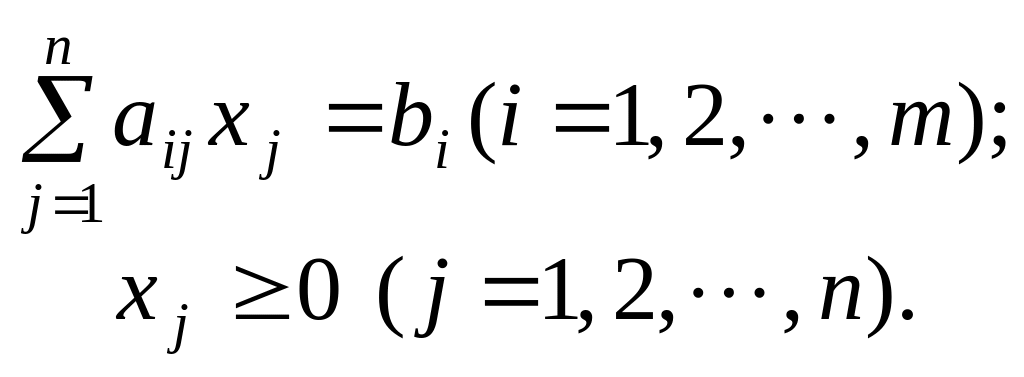 (2.6)

Ще компактнішим є запис задачі лінійного програмування у векторно-матричному вигляді:

max(min) Z = CX

за умов:

АХ = А₀; (2.7)

Х ≥ 0,

де

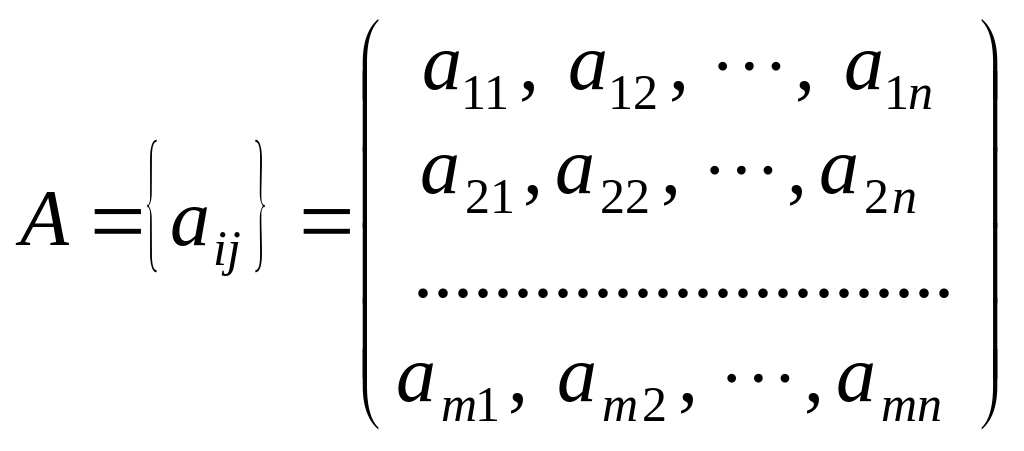
є матрицею коефіцієнтів при змінних;

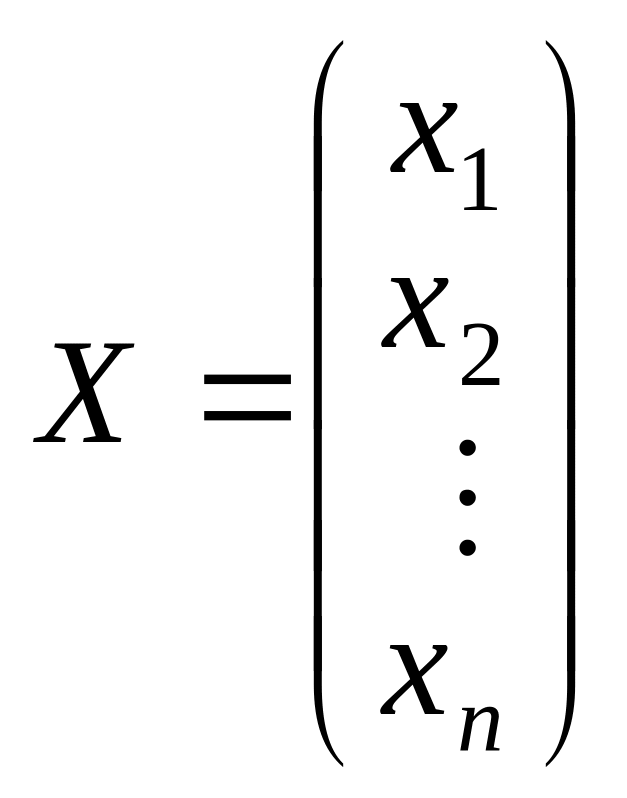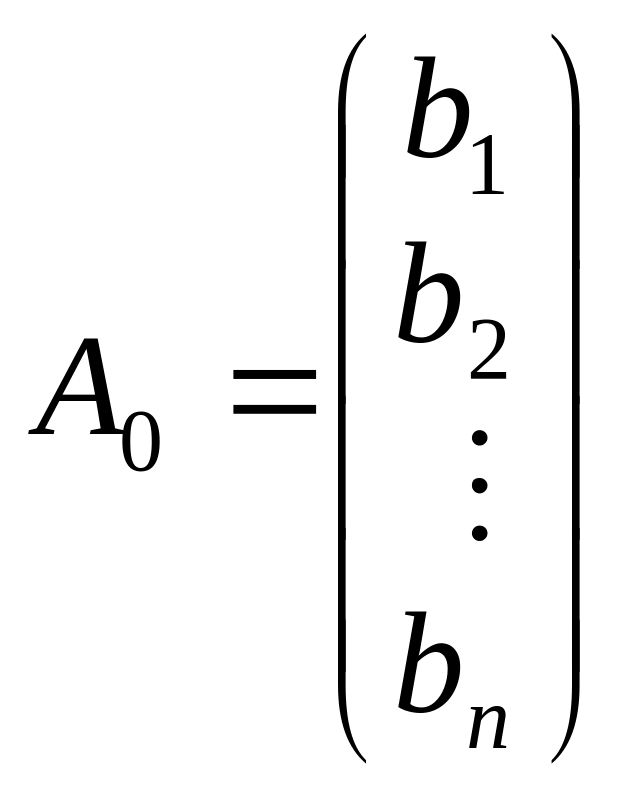— вектор змінних; — вектор вільних членів;

С = (с₁, с₂, …, с_п) — вектор коефіцієнтів при змінних у цільовій функції.

Часто задачу лінійного програмування зручно записувати у векторній формі:

max(min)Z = CX

за умов:

A₁x₁ + A₂x₂ + … + A_nx_n = A₀; (2.8)

X ≥0,

де

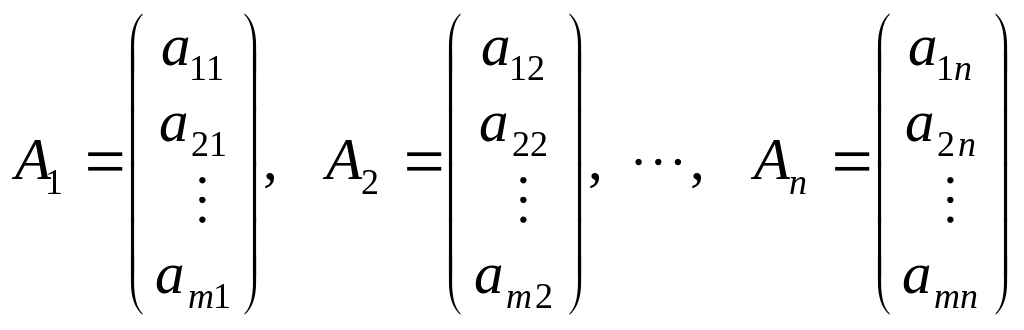
є векторами коефіцієнтів при змінних.

8. Геометрична інтерпретація задачі лінійного програмування Сукупність цих точок (розв’язків) називають багатокутником розв’язків, або областю допустимих планів (розв’язків) задачі лінйного програмування. Це може бути точка (єдиний розв’язок), відрізок, промінь, багатокутник, необмежена багатокут­на область.

Якщо в системі обмежень (2.9) буде три змінних, то кожна нерівність геометрично визначатиме півпростір тривимірного простору, граничними площинами котрого будуть a_i1x₁ + a_i2x₂ + a_i3x₃ = b_i (i = 1, 2, ...,т), а умови невід’ємності — півпростори з граничними площинами х_j = 0 (j = 1, 2, 3), де і — номер обмеження, а j — номер змінної. Якщо система обмежень сумісна, то ці півпростори як опуклі множини, перетинаючись, утворять у тривимірному просторі спільну частину, що називається багатогранником розв’язків. Він може бути точкою, відрізком, променем, багатокутником, багатогранником, багатогранною необмеженою областю.