79. Властивості оцінок параметрів

Оцінки параметрів є вибірковими характеристиками і повинні мати такі властивості:

1) незміщеності;

2) обгрунтованості;

3) ефективності;

4) інваріантності.

Означення 4.5. Вибіркова оцінка параметрів називається незміщеною, якщо вона задовольняє рівність

(4.12)

У розглядуваному випадку

Оскільки згідно з першою умовою , то . Отже, оцінка параметрів 1МНК є незміщеною.

Незміщеність — це мінімальна вимога, яка ставиться до оцінок параметрів . Якщо оцінка незміщена, то при багаторазовому повторенні випадкової вибірки попри те, що для окремих вибірок, можливо, були помилки оцінки, середнє значення цих помилок дорівнює нулю.

Різниця між математичним сподіванням оцінки і значенням оціненого параметра

(4.13)

називається зміщенням оцінки.

Не можна плутати помилку оцінки з її зміщенням. Помилка дорівнює і є випадковою величиною, а зміщення — величина стала.

Дуже важливою властивістю оцінки є її обгрунтованість.

Означення 4.6. Вибіркова оцінка параметрів А називається об­грунтованою, якщо при досить малій величині  > 0 справджується cпіввідношення

(4.14)

Іншими словами, оцінка обгрунтована, коли вона задовольняє закон великих чисел. Обгрунтованість помилки означає, що чим більші будуються вибірки, тим більша ймовірність того, що помилка оцінки не перевищуватиме достатньо малої величини .

Для обгрунтованості оцінок, здобутих на основі 1МНК, мають виконуватися три умови:

1) , де Q — додатно визначена матриця;

2) де Q — додатно визначена матриця;

3)

Третя властивість оцінок Â — ефективність — пов’язана з величиною дисперсії оцінок.

Тут доречно сформулювати важливу теорему Гаусса — Маркова, що стосується ефективності оцінки 1МНК.

Теорема Гаусса — Маркова. Функція оцінювання за методом 1МНК покомпонентно мінімізує дисперсію всіх лінійно незміщених функцій вектора оцінок :

для ,

де — дисперсія оцінок , визначених згідно з 1МНК, — дисперсія оцінок , визначених іншими методами.

Отже, функція оцінювання 1МНК у класичній лінійній моделі є найкращою (мінімально дисперсійною) лінійною незміщеною функцією оцінювання. (Цю властивість називають BLUE).

З означення дисперсії випливає, що — параметр розподілу ви­падкової величини А, яка є мірою розсіювання її значень навколо математичного сподівання.

Означення 4.7. Вибіркова оцінка параметрів А називається ефективною, коли дисперсія цієї оцінки є найменшою.

Нехай ефективна оцінка параметрів , а — деяка інша оцінка цих параметрів. Тоді

(4.15)

тобто це відношення називається ефективністю оцінки. Очевидно, що ; чим ближче до одиниці, тим ефективнішою є оцінка. Цікаво, що відношення може бути функцією сукупності спостережень , причому зі збільшенням може швидко змінюватися.

Означення 4.8. Незміщена оцінка , дисперсія якої при задовольняє умову називається асимптотично ефективною оцінкою.

Пошук ефективних оцінок параметрів — досить складна справа^*. Проте оскільки дисперсія середнього арифметичного значення оцінки, яка має вимірів, дорівнює то, як можна довести, що дає ефективну оцінку параметрів А.

Ще одна важливість оцінок — їх інваріантність.

Означення 4.8. Оцінка параметрів називається інваріант­ною, якщо для довільно заданої функції оцінка параметрів функції подається у вигляді . Іншими словами, інваріантність оцінки базується на тому, що в разі перетворення параметрів за допомогою деякої функції таке саме перетворення, виконане щодо , дає оцінку нового параметра.

Інваріантність оцінок має велике практичне значення. Наприклад, якщо відома оцінка дисперсії генеральної сукупності і вона інваріантна, то оцінку середньоквадратичного відхилення можна дістати, добувши квадратний корінь із оцінки дисперсіі. Коефіцієнт кореляції R є інваріантною оцінкою до коефіцієнта детермінації .

64. Градієнтні методи належать до наближених методів розв’язування задач нелінійного програмування і дають лише пев­не наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Зауважимо, що такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. Зрозуміло, що градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються.

В основі градієнтних методів лежить основна властивість градієнта диференційовної функції — визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.

Розглянемо метод Франка — Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.

65. Динамічне програмування являє собою математичний апарат, що дає змогу здійснювати планування багатокрокових керованих процесів, а також процесів, які розвиваються у часі.

Отже, динамічне програмування не є окремим методом розв’язування задач, а являє собою теорію, що поєднує ряд однотипних ідей та прийомів, які застосовуються для розв’язування досить різних за змістом задач.

До задач динамічного програмування належать такі, що пов’язані з оптимальним розподілом капіталовкладень, розподілом продукції між різними регіонами, визначенням найкоротшого шляху завезення товарів споживачам, задачі щодо заміни устат­кування, оптимального управління запасами тощо.

Економічні процеси можна уявити складеними з кількох етапів (кроків). На кожному з них здійснюється вплив на розвиток всього процесу. Тому у разі планування багатоетапних процесів прийняття рішень на кожному етапі має враховувати попередні зміни та бути підпорядкованим кінцевому результату. Динамічне програмування дає змогу прийняти ряд послідовних рішень, що забезпечує оптимальність розвитку процесу в цілому.

67.Планується на наступний рік діяльність виробничої системи, яка складається з n підприємств. Відома початкова сума коштів — , що має бути розподілена між всіма підприємствами. Сума вкладень х приносить k-му підприємству прибу­ток . Значення функції , задані таб­лицею.

Необхідно визначити — кошти, які потрібно виділити k-му підприємству так, щоб отримати максимальний сумарний прибуток від вкладення коштів в усі підприємства .

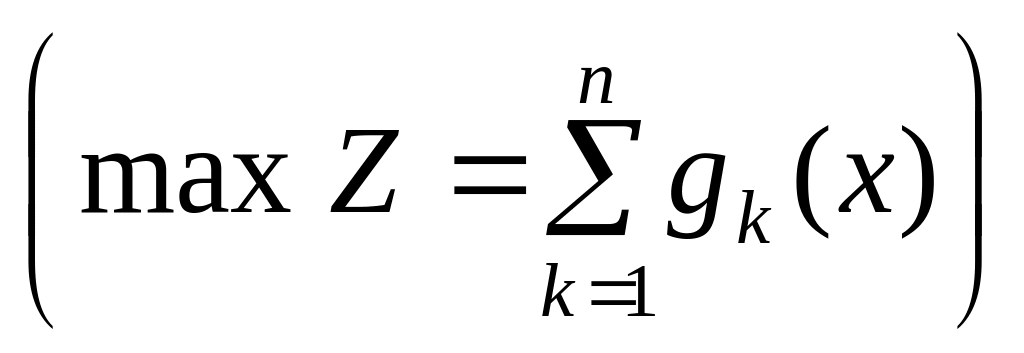Позначимо кількість коштів, що залишилися після k-го кроку (тобто кошти, які необхідно розподілити між рештою (n – k) підприємств через :

.

Задача розв’язується поетапно. В даному разі етапами є вкладення коштів в кожне підприємство.

І етап. Кошти вкладаються лише в одне (наприклад, перше) підприємство. Найбільший прибуток (ефективність першого етапу), що може бути отриманий, позначимо через . Маємо:

.

ІІ етап. Порівняємо ефективність, яку отримаємо, вкладаючи кошти лише у перше підприємство та вкладаючи кошти одночасно і в перше, і в друге підприємства. Якщо позначити ефективність другого етапу через , то отримаємо:

.

Для k-го етапу маємо рекурентне співвідношення:

.

Послідовно розв’язуючи отримані рівняння, визначаємо оптимальні рішення на кожному етапі.

73. Роль економетричного дослідження визначається тими задачами, які може розв'язувати економетрія.

Найважливішою задачею є оцінювання параметрів і перевірка значущості економетричної моделі. Першим етапом цього процесу є специфікація моделі в математичній формі. Другий етап — збір і підготовка економічної інформації. На третьому етапі оцінюються параметри моделі. Четвертий етап — це перевірка моделі на достовірність. Дуже важливими на цьому етапі є оцінки дисперсії залишків моделі. Ці оцінки відіграють вирішальну роль при з'ясуванні якості економетричних моделей, вони необхідні для визначення надійності обчислених параметрів і для застосування розроблених моделей у прогнозуванні.

74. Сучасні методи управління економічними системами та процесами базуються на широкому використанні математичних методів та ЕОМ. Сформувався напрямок теоретично-практичних досліджень — економіко-математичне моделювання. Математичне моделювання є вираженням процесу математизації наукового економічного знання. Математика, проникаючи в сутність економічної науки, приносить із собою точність та універсальність розв'язків, строгість і довершеність наукових концепцій. З розвитком математики, електронної обчислювальної техніки, загальнометодологічних та економічної наук дедалі ширше використовують математичні моделі.

Математична модель об'єкта (процесу, явища) містить у собі три групи елементів:

1) характеристику об'єкта, який потрібно визначити (невідомі величини), — вектор Y= ;

2) характеристики зовнішніх (щодо модельованого об'єкта) умов, які змінюються, — вектор X=( );

3) сукупність внутрішніх параметрів об'єкта — А.

Множини умов та параметрів X і А можуть розглядатись як екзогенні величини (тобто такі, які визначаються поза рамками моделі), а величини, що належать вектору Y, — як ендогенні (тобто такі, які визначаються за допомогою моделі).

Математичну модель можна тлумачити як особливий перетворювач зовнішніх умов об'єкта X (входу) на характеристики об'єкта Y (виходу), які мають бути знайдені.

Залежно від способу вираження співвідношень між зовнішніми умовами, внутрішніми параметрами та характеристиками, які мають бути знайдені, математичні моделі поділяються на дві групи: структурні та функціональні.

Структурні моделі відбивають внутрішню організацію об'єкта: його складові частини, внутрішні параметри, їх зв'язок з «входом» і «виходом» і т. ін. Розрізняють три види структурних моделей:

(3.1) (3.2)

3) імітаційні моделі.

В імітаційних моделях невідомі величини визначаються також одночасно із вхідними параметрами, але конкретний вигляд співвідношень невідомий.

Моделі типу (3.1) — (3.2) можна розв'язати з допомогою чисельних алгоритмів. Можливості побудови таких моделей (3.1) дуже обмежені. Для розв'язування задачі (3.2), яка не зводиться до задачі (3.1), необхідно мати спеціальний алгоритм, за яким не тільки знаходять розв'язки, а й виявляють загальні властивості розв'язків, які не залежать від конкретних параметрів задачі.

Імітаційні моделі не зводяться до чітко визначених математичних задач, а тому потрібно знаходити особливі способи для одержання розв'язків. Такі моделі виникають при спробах дати математичний опис особливо складних об'єктів (складних систем). Імітаційні моделі не мають чіткого зображення внутрішньої організації (структури) об'єкта, і тому їм належить проміжне місце між структурними та функціональними моделями.

Основна ідея функціональних моделей — пізнання сутності об'єкта через найважливіші прояви цієї сутності: діяльність, функціонування, поведінку. Внутрішня структура об'єкта при цьому не вивчається, а тому інформація про структуру не використовується. Функціональна модель описує поводження об'єкта так, що задаючи значення «входу» X, можна дістати значення «виходу» Y (без участі інформації про параметри):

Y = А(Х). (3.3)

Побудувати функціональну модель — означає знайти оператор А, який пов'язує X і У.

Економетричні моделі належать до функціональних моделей. Вони кількісно описують зв'язок між вхідними показниками економічної системи (X) та результативним показником (Y). У загальному вигляді економетричну модель можна записати так:

Y=f(X,u),

де X — вхідні економічні показники; u — випадкова або стохастична складова.

Показники X найчастіше бувають детермінованими. Адитивна складова u є випадковою змінною, а отже, з огляду на те, що залежна змінна Y залежить від u, вона також є стохастичною. Звідси випливає висновок: економетрична модель є стохастичною.

Побудова і дослідження економетричних моделей мають ряд особливостей. Ці особливості пов'язані з тим, що економетричні моделі є стохастичними. Вони кількісно описують кореляційно-регресійний зв'язок між економічними величинами. Отже, щоб побудувати економетричну модель, необхідно:

1) мати достатньо велику сукупність спостережень даних;

2) забезпечити однорідність сукупності спостережень;

3) забезпечити точність вхідних даних.

Розрізняють три способи формування вибірки: часову, просторову і просторово-часову.

Якщо сукупність спостережень вивчається у статиці (просторова вибірка), то всі дані можна зобразити у вигляді матриці розміром n x m , в якій кожний рядок несе інформацію про одиницю вибіркової сукупності, а стовпець характеризує певну ознаку.

Часова вибірка містить набір значень ознак функціонування окремого об'єкта в динаміці m х Т, тобто по суті складається з двовимірного чи багатовимірного часового ряду.

Просторово-часова вибірка є комбінацією просторової і часової вибірок n x m х T.

Економетричне моделювання базується на професійних знаннях про об'єкт дослідження. До завдань попереднього аналізу належить вирішення таких основних питань:

1) визначення набору змінних, які описують процес функціонування досліджуваних об'єктів;

2) аналіз взаємозв'язків між окремими змінними;

3) вибір раціонального типу економетричної моделі.

Питання вибору результативних ознак (економічних показників), що моделюються, вирішується відносно просто. Вони часто задані формулюванням мети дослідження. Вибір незалежних змінних (ознак-факторів) є процесом послідовного уточнення початкової гіпотези. У цьому процесі можна вирізнити такі етапи: формування початкової гіпотези про набір незалежних змінних; експертна оцінка цього набору; аналіз взаємозв'язків; добір і звуження кола істотних для моделювання змінних.

В основу формування початкової гіпотези про набір змінних покладено загальну схему функціонування об'єкта, що моделюється. На перелік змінних, які вносяться до початкового набору, враховується призначення моделі, тип дослідження і т. ін.

Звуження початкового набору змінних — процес багатостадійний, який відбувається на всіх етапах побудови моделі: під час проведення апріорного аналізу і формування робочої гіпотези (ще до збору вхідних даних), на етапі їх попереднього аналізу й перетворення і навіть на етапі побудови моделі

75. Розглянемо економетричну модель з двома змінними у загальному вигляді: Y =f(X) + u, де Y — залежна змінна; X — незалежна змінна; u — випадкова складова. Це означає, що ми ідентифікували змінну X, яка впливає на змінну Y. Назвемо таку економетричну модель простою моделлю. На базі простої економетричної моделі розглянемо принципову структуру економетричної моделі та основні методи оцінювання її параметрів. Теоретичні знання про взаємозв'язок між економічними показниками (модель (1)) мають підказати його конкретну аналітичну форму. Але оскільки одні й ті самі економічні процеси можуть бути описані різними функціями, то потрібно звернутися до статистичного аналізу і з його допомогою зробити вибір серед можливих альтернативних варіантів. Найпростішою є лінійна форма зв'язку між двома змінними:

,

де і — невідомі параметри.

Можливі й інші форми залежностей між двома змінними, наприклад:

.

Останнє з цих співвідношень є лінійним відносно , а перші два можна звести до лінійної форми, якщо взяти логарифми від виразів в обох частинах кожного з рівнянь:

;

.

Навіть побіжне знайомство з економічними показниками, взаємозв'язок між якими вимірюється, показує, що окремі експериментальні значення залежної змінної не можуть міститися строго на прямій лінії чи на графіку функції іншої форми. Певна частина фактичних спостережень над змінною лежатиме вище або нижче від значень, обчислених згідно з вибраною функцією. Якщо фактичні значення залежної змінної містяться на значній відстані від обчислених з допомогою функції, то можна припустити, що формалізація залежності між економічними показниками на основі функції типу (1) чи якоїсь іншої функції не адекватна реальному процесу взаємозв'язків у економіці. Проте поняття «значна відстань» не є конкретним, а тому не може бути критерієм для оцінювання адекватності моделі.

Щоб розв'язати цю задачу, до економетричної моделі вводять стохастичну складову, яка акумулює в собі всі відхилення фактичних спостережень змінної Y від обчислених згідно з моделлю.

Математичний аналіз цієї складової дасть змогу зробити висновок щодо того, чи можна вважати її стохастичною і чи містить вона систематичну частину відхилень, яка може бути зумовлена наявністю тих чи інших помилок у моделюванні.

Нехай вектор змінної Y описує витрати на споживання, а вектор X — величину доходу сім'ї. Очевидно, що для окремих груп сімей існує певна залежність між споживчими витратами і доходом сім'ї. Проте, як уже зазначалося, на розмір споживчих витрат крім доходу можуть впливати інші фактори, частина яких є випадковими. Ці фактори й зумовлюють відхилення фактичних витрат на споживання від обчислених, наприклад, на основі регресійної функції:

(2)

Наблизити обчислені значення до фактичних формально можна введенням до моделі стохастичної складової:

. (3)

У моделі (3) символом u позначено змінну, яка може набувати додатних та від'ємних значень, оскільки вона вимірює відхилення витрат на споживання кожної окремої сім'ї від обчисленого значення згідно з (2).

Зауважимо, що в моделі (3) а₀ і а1 — оцінювані параметри, а в моделі (2) і —їх оцінки.

Стохастичну складову u економетричної моделі називають похибкою (залишком, збуренням, відхиленням).

Введення до моделі (3) стохастичної складової має три підстави, кожна з яких не виключає решти двох.

1. Величину витрат на споживання визначає не лише рівень доходів, а й інші об'єктивні чинники, наприклад розмір сім'ї, середній вік і т. ін.

2. На величину споживання впливають випадкові фактори, наприклад схильність до ощадливості, стриманість чи навпаки — надмірність у витратах і т. ін.

3. Частина факторів, які впливають на величину споживчих витрат, не оцінюються кількісно, вони не квантифікуються. Крім того, можлива помилка вимірювання змінних.

Отже, замість залежності

,

де m — досить велике, розглядається модель з невеликим числом незалежних_змінних, причому Y є функцією від найважливіших із =(j = l,m), тоді чистий сумарний ефект від впливу всіх інших чинників відбиває змінна u. У крайньому разі, якщо залишається одна незалежна змінна, маємо:

Y=f(X,u). (4)

У класичній лінійній економетричній моделі змінна u інтерпретується як випадкова змінна, яка має розподіл з математичним сподіванням, що дорівнює нулю, і сталою дисперсією . Це дає змогу розглядати змінну u як стохастичне збурення (похибку, відхилення). З огляду на те, що u охоплює вплив багатьох чинників, які можна вважати незалежними, на підставі центральної граничної теореми теорії ймовірностей, доходимо висновку: стохастична складова економетричної моделі розподілена за нормальним законом.

В економетричній моделі (2) оцінки параметрів а₀, а1 невідомі. На підставі вибіркових спостережень X і Y потрібно оцінити ці параметри і перевірити виконання щодо них деяких гіпотез.

80. У класичній регресійній моделі Y = ХА + u; вектор u = (u1,u2,…,un) і залежний від нього вектор Y = (у1, у₂,..., уn)' є випадковими змінними. До оператора оцінювання входить вектор , а отже, оператор також можна вважати випадковою функцією оцінювання параметрів моделі.

Відомо, що для характеристики випадкових змінних , поряд з математичним сподіванням, застосовуються також дисперсія і коваріація . Істинні значення цих параметрів класичної економетричної моделі утворюють дисперсійно-коваріаційну матрицю:

Нагадаємо означення варіації і коваріації:

,

Оцінки коваріаційної матриці var( )= використовуються для знаходження стандартних помилок та обчислення довірчих інтервалів оцінок параметрів . Вони використовуються й при перевірці їх статистичної значущості.

На головній діагоналі матриці var ( ) містяться оцінки дисперсій j-ї оцінки параметрів, що ж до елементів , які розміщені поза головною діагоналлю, то вони є оцінками коваріації між .

Оскільки вектор залишків , то можна записати так:

Позначимо (j,k)-й елемент матриці (X' X)^-1 символом , тоді j-й елемент по головній діагоналі матриці var( ) обчислюється за формулою:

Коваріації , що містяться за межами головної діагоналі, відповідно такі:

П РОГНОЗ Використаємо модель для знаходження прогнозних значень вектора , який відповідатиме очікуваним значенням матриці незалежних змінних . Наш прогноз може бути точковим або інтервальним. Розглянемо спочатку точковий прогноз і припустимо, що ми визначили його як деяку лінійну функцію від , тобто

Оскільки Y = ХА + u, то незміщена точкова оцінка прогнозу M[Y₀(X₀)] = X₀A + u,

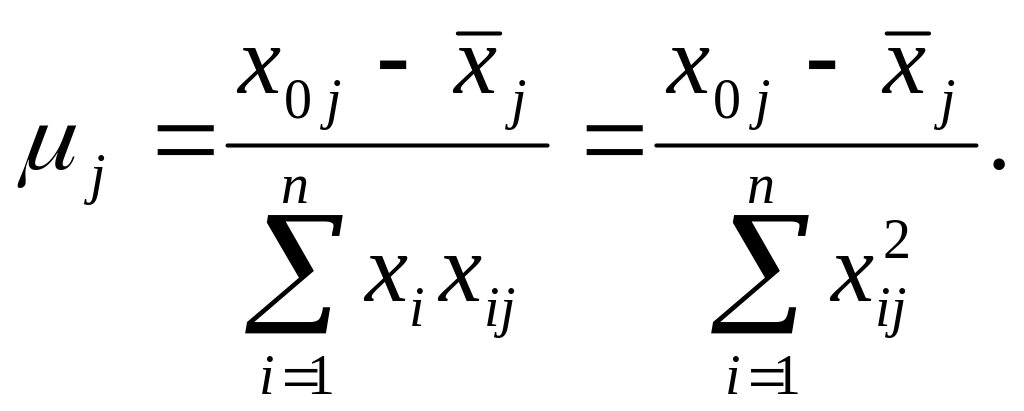
Щоб отримати інтервальний прогноз необхідно розрахувати середню похибку прогнозу.

Вона зростає з віддаленням значення x_0j від відповідного середнього значення вибірки.

У матричному вигляді дисперсія прогнозу

Середньоквадратична помилка прогнозу .

Довірчий інтервал для прогнозних значень .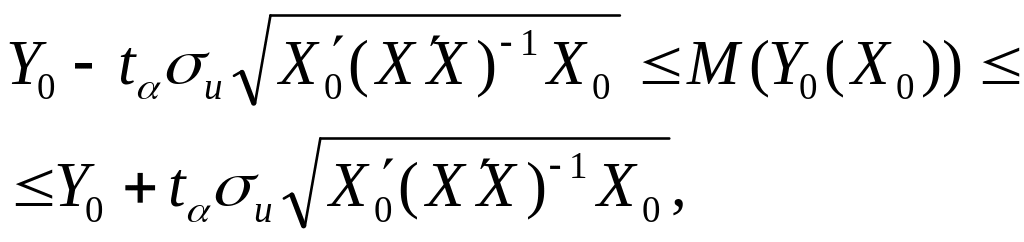

Зауважимо, що можна розглядати як точкову оцінку математичного сподівання прогнозного значення Y₀, а також як індивідуальне значення Y₀ для вектора незалежних змінних Х₀, що лежить за межами базового періоду.

Для визначення інтервального прогнозу індивідуального значення необхідно знайти відповідну стандартну похибку .

Отже, інтервальний прогноз індивідуального значення визначається як

81. При оцінці взаємозв'язку між двома змінними за допомогою 1МНК звертають увагу на коефіцієнти кореляції. Із теорії статистики відомо, що

, де — парний коефіцієнт кореляції між Y та X; — середньо-квадратичне відхилення залежної змінної; — середньоквадратичне відхилення незалежної змінної.

Отже, оцінка параметрів моделі прямо пропорційна до коефіцієнта парної кореляції. Аналогічні співвідношення виконуються і в загальному випадку.

А це означає, що оцінити параметри моделі можна через коефіцієнти кореляції: спочатку оцінити тісноту зв'язку між кожною парою змінних, а потім знайти оцінки параметрів економетричної моделі.

Залежність оцінок параметрів економетричної моделі й коефіцієнтів парної кореляції покладено в основу алгоритму покрокової регресії.

Покроковий регресійний аналіз – один з багатьох методів побудови регресійної моделі, який використовується, коли треба оптимізувати процес побудови.

Опишемо цей алгоритм.

Крок 1-й. Усі вхідні дані змінних стандартизують (нормалізують):

де - нормалізована залежна змінна; — нормалізовані незалежні змінні; — середнє значення j-ї незалежної змінної; — середнє значення При цьому середні значення і дорівнюють нулю, а дисперсії — одиниці.

Крок 2-й. Знаходять кореляційну матрицю (матриця парних коефіцієнтів кореляції):

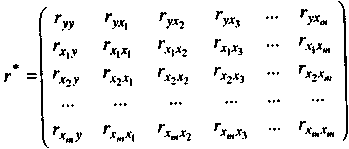
де — парні коефіцієнти кореляції між залежною і незалежними змінними, де п — кількість спостережень; — парні коефіцієнти кореляції між незалежними змінними,

Крок 3-й. На підставі порівняння абсолютних значень вибирають . Найбільше вказує на ту незалежну змінну, яка найтісніше пов'язана з у. З допомогою 1МНК знаходять оцінку параметрів цієї моделі: де — оцінки параметрів моделі, яка будується на основі нормалізованих даних.

Крок 4-й. Серед тих, що залишилися, значень вибирається максимальне і в модель вводиться наступна незалежна змінна х_е

Якщо немає обмеження на введення в економетричну модель кожної наступної незалежної змінної, то обчислення виконуються доти, поки поступово не будуть введені в модель усі змінні.

Сума квадратів залишків дорівнює:

Звідси мінімізації підлягає

Узявши похідну за кожним невідомим параметром цієї функції і прирівнявши всі здобуті похідні нулю, дістанемо систему нормальних рівнянь.

Система нормальних рівнянь для знаходження параметрів моделі в загальному вигляді запишеться так:

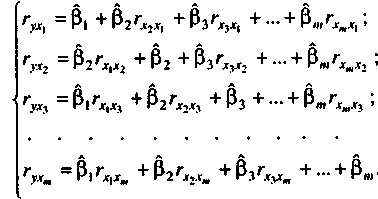
Позначимо матрицю парних коефіцієнтів кореляції між незалежними змінними через г, а вектор парних коефіцієнтів кореляції між залежною і незалежними змінними через . Тоді система нормальних рівнянь набере вигляду

а оператор оцінювання параметрів:

Оскільки всі змінні нормалізовані, то параметри показують порівняльну силу впливу кожної незалежної змінної на залежну: чим більше за модулем значення параметра , тим сильніше впливає j-та змінна на результат.

Зв'язок між оцінками параметрів моделі на основі нормалізованих і ненормалізованих змінних запишеться так:

82. Тіснота зв'язку загального впливу всіх незалежних змінних на залежну визначається коефіцієнтами детермінації і множинної кореляції.

Щоб дати метод їх розрахунку необхідно показати, що варіація залежної змінної (Y) навколо свого вибіркового середнього значення ( )* може бути розкладена на дві складові:

1) варіацію розрахункових значень ( ) навколо середнього значення ( );

2) варіацію розрахункових значень ( ) навколо фактичних (Y). Необхідні при цьому обчислення зведемо в табл. 1.

Всі змінні Y і X взяті як відхилення від свого середнього значення.

Використаємо середні квадратів відхилень (дисперсії) (див. табл. 1) і запишемо формулу для обчислення коефіцієнта детермінації:

або, не враховуючи ступенів свободи:

Оскільки задані незміщені оцінки дисперсії з урахуванням числа ступенів свободи, то коефіцієнт детермінації може зменшуватись при введені в модель нових незалежних змінних. Тоді як для коефіцієнта детермінації, обчисленого без урахування поправки (п - 1 /т - 1) на число ступенів свободи (2.2), коефіцієнт детермінації ніколи не зменшується. Залежність між цими двома коефіцієнтами можна подати так:

де R² — коефіцієнт детермінації з урахуванням числа ступенів свободи; — коефіцієнт детермінації без урахування числа ступенів свободи.

Для функції з двома і більше незалежними змінними коефіцієнт детермінації може набувати значень на множині є ]0,1[. Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної (Y) визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних. Множинний коефіцієнт кореляції:

Він характеризує тісноту зв'язку всіх незалежних змінних із залежною.Для множинного коефіцієнта кореляції з урахуванням і без урахування числа ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації.Розглянемо альтернативний спосіб обчислення коефіцієнтів детермінації і кореляції, коли система нормальних рівнянь будується на основі коефіцієнтів парної кореляції r.

У такому разі оцінку параметрів моделі можна записати: де — алгебраїчне доповнення матриці r до елемента r_kj.

Сума квадратів відхилень (залишків) також може бути виражена через алгебраїчне доповнення матриці г:

де |г|—-визначник кореляційної матриці. А це, у свою чергу, дає нам альтернативний вираз для коефіцієнта детермінації:

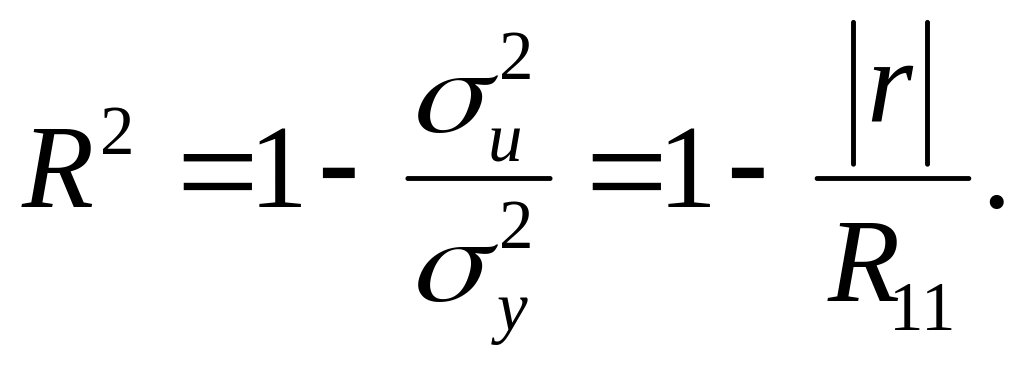
Ще один альтернативний метод розрахунку коефіцієнтів детермінації на основі матриці r можна подати у виґляді

Звідси коефіцієнт кореляції

ЧАСТИННІ КОЕФІЦІЄНТИ КОРЕЛЯЦІЇ І КОЕФІЦІЄНТИ РЕГРЕСІЇ Частинні коефіцієнти кореляції так само, як і парні, характеризують тісноту зв'язку між двома змінними. Але на відміну від парних частинні коефіцієнти характеризують тісноту зв'язку за умови, що інші незалежні змінні сталі.

Можна дістати спрощений вираз для розрахунку коефіцієнта частинної кореляції, обравши інший спосіб інтерпретації цього коефіцієнта. Для випадку простої регресії двох змінних маємо

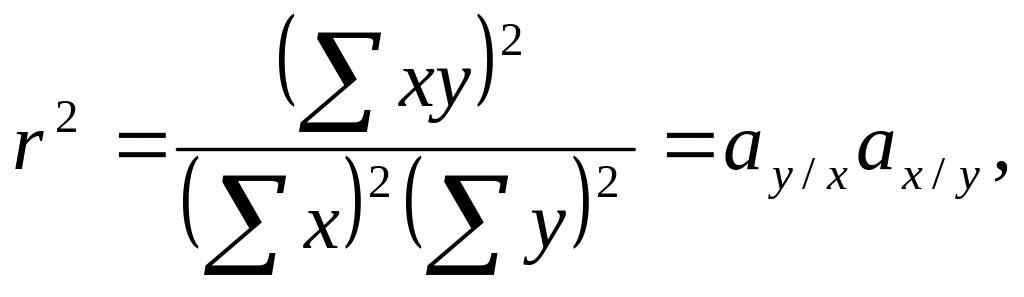
де характеризує коефіцієнт при х у рівнянні y = f(x), а — коефіцієнт при у в рівнянні х = f(y). Отже, квадрат коефіцієнта парної кореляції дорівнює добутку двох наведених коефіцієнтів. Коефіцієнт частинної кореляції можна визначити аналогічно. Наприклад, розглянемо два регресійні рівняння: y = f(x₂,x₃); x₂ = f(y,x₃). Нехай в цих рівняннях x₃ дорівнює деякій довільній величині с, тоді член, який відповідає змінній x₃ збігатиметься з вільним членом, а отже, дістанемо дві прості регресії, які відбивають загальну зміну у і х₂ на площині х₃ = с. Оскільки модель є лінійною, то коефіцієнти регресії x₂ = f(y) і y-f(x₂) лишаються незмінними при різних значеннях с, тобто можна стверджувати: квадрат коефіцієнта частинної кореляції між у і х₂ дорівнює добутку коефіцієнтів при х₂ і у у двох множинних регресіях. Запишемо ці рівняння у вигляді

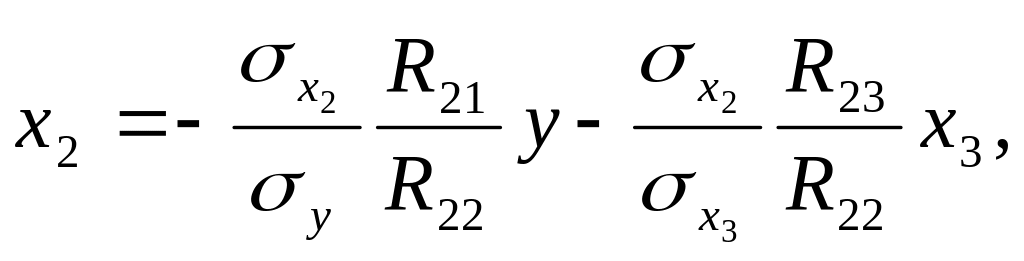Звідси

Для знаходження частинного коефіцієнта кореляції змінної у з х₂ за умови, що змінна стала, достатньо взяти добуток параметрів при і у в наведених щойно рівняннях з протилежним знаком.

Тоді частинні коефіцієнти кореляції будуть такі:

Ці висновки можна поширити на випадок, коли економетрична модель має т незалежних змінних (j = 1,m), але при цьому решта незалежних змінних (крім двох) є константами.

83. Значущість економетричної моделі Гіпотезу про рівень значущості зв'язку між залежною і незалежною змінними можна перевірити з допомогою F-критерію:

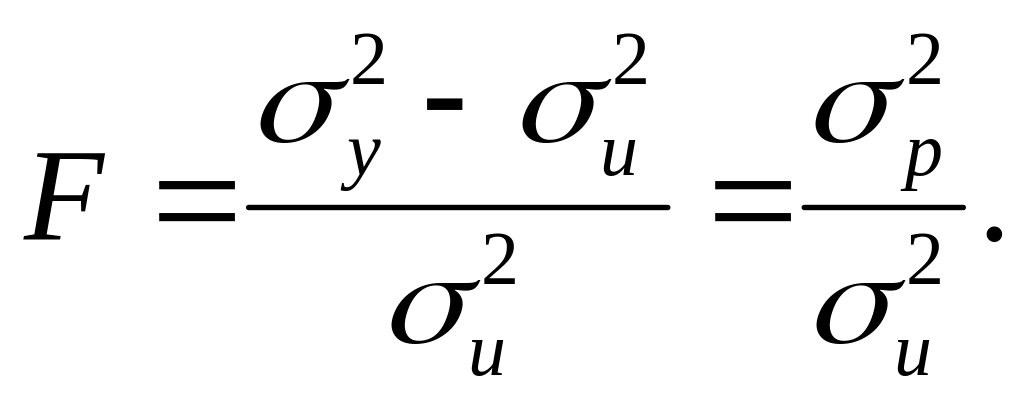
При цьому ми виходимо з того, що залишки u розподілені нормально, тобто користуємося фундаментальною теоремою про те, що для нормально розподіленої випадкової величини з нульовою середньою і одиничною дисперсією сума квадратів її п випадково вибраних значень має розподіл з п ступенями свободи. Фактичне значення F-критерію порівнюється з табличним при ступенях свободи m - 1 і n - m і вибраному рівні значущості. Якщо , то гіпотеза про істотність зв'язку між залежною і незалежними змінними економетричної моделі підтверджується, у противному разі — відкидається.

а також формулою для обчислення коефіцієнта детермінації запишемо альтернативну форму F-критерію:

Згідно з цим критерієм перевіряється значущість коефіцієнта детермінації, а отже, й усієї моделі.

Значущість коефіцієнта кореляції Оскільки коефіцієнт кореляції є також вибірковою характеристикою, яка може відхилятись від свого «істинного» значення, значущість коефіцієнта кореляції також потребує перевірки. Базується вона на t-критерії

де R² — коефіцієнт детермінації моделі; R — коефіцієнт кореляції; п-т—число ступенів свободи.

Якщо > t_табл(а), де t_та6л(а) — відповідне табличне значення t-роз-поділу з п-т ступенями свободи, то можна зробити висновок про значущість коефіцієнта кореляції між залежною і незалежними змінними моделі.

Значущість оцінок параметрів моделі Перевіримо значущість оцінок параметрів і знайдемо для них довірчі інтервали, припустивши для цього, що залишки u нормально розподілені, тобто . Тоді параметри моделі задовольняють багатовимірний нормальний розподіл:

Коли відома величина , то цей результат можна буде використати для перевірки значущості елементів вектора та оцінювання довірчих інтервалів елементів цього вектора. Проте дисперсія , невідома, а отже, потрібно розглянути методи її знаходження.

Для цього визначимо залишки:

Таким чином, залишки, які можна дістати на підставі експериментальних даних, записано у вигляді лінійних функцій від невідомих залишків е. Тоді суму квадратів відхилень подамо у вигляді

де N — симетрична ідемпотентна матриця.

У цих перетвореннях ми виходили з того, що N є симетричною ідемпотентною матрицею, оскільки Е_п — одинична матриця, а —симетрична розміром n x m. Знайдемо математичне сподівання для обох частин рівняння і застосуємо спочатку властивість, яка полягає в тому, що , де tr (N) — слід матриці N,

З огляду на сказане маємо:

У цьому співвідношенні матриця має порядок т, добуток дорівнює Е_т, а її слід дорівнює т. Звідси Нарешті, лишилося показати, що сума квадратів залишків розподілена незалежно від . Для цього знайдемо коваріацію між залишками і :

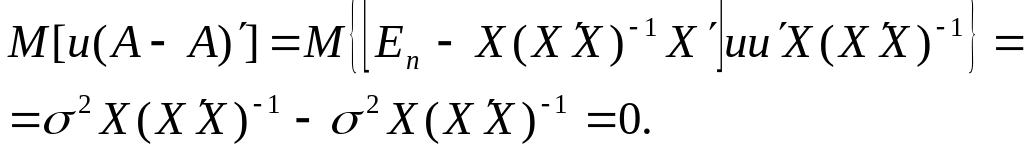Оскільки u і - лінійні функції від нормально розподілених змінних, то вони також розподілені нормально і, як було показано, їх коваріації дорівнюють нулю.

Це дає нам змогу скористатися t-розподілом для перевірки гіпотез відносно істотності кожного з параметрів економетричної моделі

Перевірку гіпотези виконаємо згідно з t-критерієм: де — діагональний елемент матриці .

— називається стандартною похибкою оцінки параметра моделі.

Обчислене значення t-критерію порівнюється з табличним при вибраному рівні значущості і n-m ступенях свободи. Якщо , то відповідно оцінка параметра економетричної моделі є достовірною. На основі t-критерію і стандартної помилки побудуємо довірчі інтервали для параметрів :

84. Однією з чотирьох умов, які необхідні для оцінювання параметрів загальної лінійної моделі 1МНК, є умова , яка стосується матриці вихідних даних X. А саме, незалежні змінні моделі утворюють лінійно незалежну систему векторів, тобто вони не повинні бути мультиколінеарними: Це означає,що серед пояснювальних змінних моделі не повинно бути лінійно залежних. Проте на практиці вони дуже часто пов'язані між собою. Тому в економетричних дослідженнях вельми важливо з'ясувати, чи існують між пояснювальними змінними взаємозв'язки, які називають мультиколінеарністю.

Мультиколінеарність означає існування тісної лінійної залежності, або сильної кореляції, між двома чи більше пояснювальними змінними.

Вона негативно впливає на кількісні характеристики економетричної моделі або робить її побудову взагалі неможливою.

Так, мультиколінеарність пояснювальних змінних призводить до зміщення оцінок параметрів моделі, через що з їх допомогою не можна зробити коректні висновки про результати взаємозв'язку залежної і пояснювальних змінних.

Основні наслідки мультиколінеарності.

1. Падає точність оцінювання, яка виявляється так:

а) помилки деяких конкретних оцінок стають занадто великими;

б) ці помилки досить корельовані одна з одною;

в) дисперсії оцінок параметрів різко збільшуються.

2. Оцінки параметрів деяких змінних моделі можуть бути незначущими через наявність їх взаємозв'язку з іншими змінними, а не тому, що вони не впливають на залежну змінну. У такому разі множина вибіркових даних не дає змоги цей вплив виявити.

3. Оцінки параметрів стають досить чутливими до обсягів сукупності спостережень. Збільшення сукупності спостережень іноді може спричинитися до істотних змін в оцінках параметрів.

З огляду на перелічені наслідки мультиколінеарності при побудові економетричної моделі потрібно мати інформацію про те, що між пояснювальними змінними не існує мультиколінеарністі.

ОЗНАКИ МУЛЬТИКОЛІНЕАРНОСТІ

1) Коли серед парних коефіцієнтів кореляції пояснювальних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це означає можливість існування мультиколінеарності. Інформацію про парну залежність може дати симетрична матриця коефіцієнтів парної кореляції або кореляції нульового порядку між пояснювальними змінними:

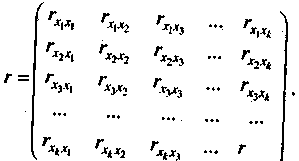Проте коли до моделі входять більш як дві пояснювальні змінні, то вивчення питання про мультиколінеарність не може обмежуватись інформацією, що її дає ця матриця. Явище мультиколінеарності в жодному разі не зводиться лише до існування парної кореляції між незалежними змінними. Більш загальна перевірка передбачає знаходження визначника (детермінанта) матриці r, який називається детермінантом кореляції і позначається |г|. Числові значення детермінанта кореляції задовольняють умову: | г | [0,1].

2) Якщо | r |= 0, то існує повна мультиколінеарність, а коли | r | =1, мультиколінеарність відсутня. Чим ближче | r | до нуля, тим певніше можна стверджувати, що між пояснювальними змінними існує мультиколінеарність. Незважаючи на те, що на числове значення | r | впливає дисперсія пояснювальних змінних, цей показник можна вважати точковою мірою рівня мультиколінеарності.

3) Якщо в економетричній моделі знайдено мале значення параметра при високому рівні частинного коефіцієнта детермінації і при цьому F-критерій істотно відрізняється від нуля, то це також свідчить про наявність мультиколінеарності.

4) Коли коефіцієнт частинної детермінації R , який обчислено для регресійних залежностей між однією пояснювальною змінною та іншими, має значення, яке близьке до одиниці, то можна говорити про наявність мультиколінеарності.

5) Нехай при побудові економетричної моделі на основі покрокової регресії введення нової пояснювальної змінної істотно змінює оцінку параметрів моделі при незначному підвищенні (або зниженні) коефіцієнтів кореляції чи детермінації. Тоді ця змінна перебуває, очевидно, у лінійній залежності від інших, які було введено до моделі раніше. Усі ці ознаки мультиколінеарності мають один спільний недолік: ні одна з них чітко не розмежовує випадки, коли мультиколінеарність істотна і коли нею можна знехтувати.

85. Найповніше дослідити мультиколінеарність можна з допомогою алгоритму Фаррара—Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється мультиколінеарність усього масиву незалежних змінних ( — «хі»-квадрат); кожної незалежної змінної з рештою змінних (F-критерій); кожної пари незалежних змінних (t-критерій).Усі ці критерії при порівнянні з їх критичними значеннями дають змогу робити конкретні висновки щодо наявності чи відсутності мультиколінеарності незалежних змінних.Опишемо алгоритм Фаррара—Глобера.

Крок 1. Стандартизація (нормалізація) змінних.

Позначимо вектори незалежних змінних економетричної моделі через ,х₂,х₃ ...х_т . Елементи стандартизованих векторів обчислимо за формулами:

1) = 2) = 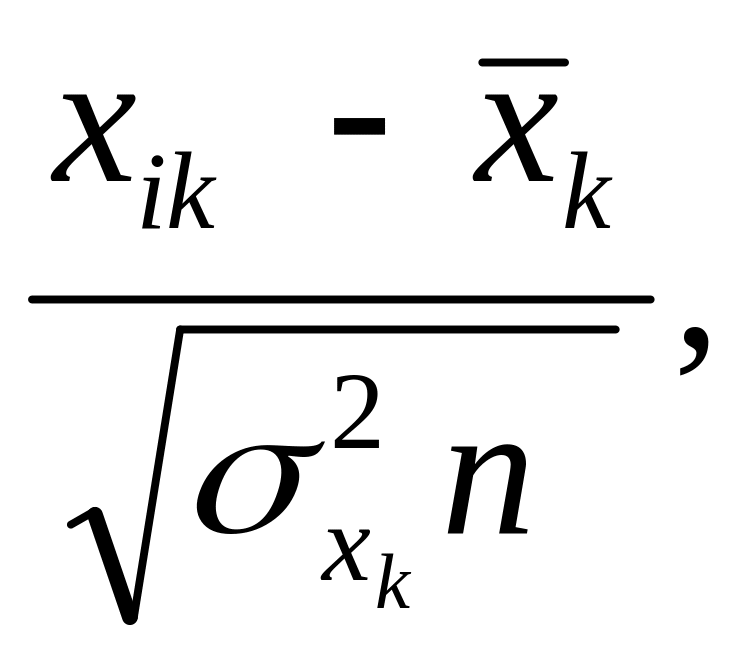де n — число спостережень (i = 1,n); т — число пояснювальних змінних, (k = 1, m); — середнє арифметичне -ї пояснювальної змінної; — дисперсія k-i пояснювальної змінної.

Крок 2. Знаходження кореляційної матриці, виходячи з двох методів нормалізації змінних

1) ; 2) де — матриця стандартизованих незалежних (пояснювальних) змінних, —матриця, транспонована до матриці .

Крок 3. Визначення критерію («хі»-квадрат):

де — визначник кореляційної матриці r.

Значення цього критерію порівнюється з табличним при ступенях свободи і рівні значущості . Якщо то в масиві пояснювальних змінних існує мультиколінеарність.

Крок 4. Визначення оберненої матриці:

Крок 5. Обчислення F-критеріїв:

де — діагональні елементи матриці С. Фактичні значення критеріїв порівнюються з табличними при п - т і т - 1 ступенях свободи і рівні значущості . Якщо , то відповідна k-та незалежна змінна мультиколінеарна з іншими.

Коефіцієнт детермінації для кожної змінної

Крок 6. Знаходження частинних коефіцієнтів кореляції:

, де — елемент матриці С, що міститься в k-му рядку і j-му стовпці; і — діагональні елементи матриці С.

Крок 7. Обчислення t-критеріїв:

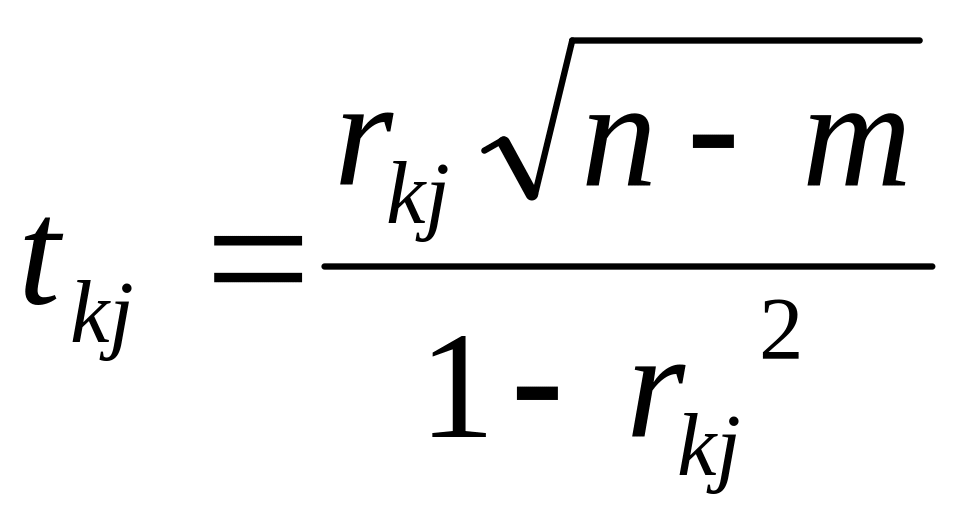. Якщо > , то між незалежними змінними і існує мультиколінеарність.

Якщо F-критерій більший за табличне значення, тобто коли k-та змінна залежить від усіх інших у масиві, то необхідно вирішувати питання про її вилучення з переліку змінних.

Якщо — критерій більший за табличний, то ці дві змінні (k і j) тісно пов'язані одна з одною. Звідси, аналізуючи рівень обох видів критеріїв F і t, можна зробити обгрунтований висновок про те, яку зі змінних необхідно вилучити з дослідження або замінити іншою. Проте заміна масиву незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження.

86. Цей метод призначений для оцінювання моделей великого розміру, а також для оцінки параметрів моделі, якщо до неї входять мультиколінеарні змінні.Існують різні модифікації методу головних компонентів, які різняться між собою залежно від того, що береться за основу при визначенні ортогональних змінних — коваріаційна чи кореляційна матриця незалежних змінних. Нехай маємо матрицю X, яка описує незалежні змінні моделі. Оскільки спостереження, що утворюють матрицю X, як правило, корельовані між собою, то можна поставити питання про кількість реально незалежних змінних, які входять до цієї матриці. Точніше, ідея методу полягає в тому, щоб перетворити множину змінних X на нову множину попарно некорельованих змінних, серед яких перша відповідає максимально можливій дисперсії, а друга — максимально можливій дисперсії в підпросторі, який є ортогональним до першого, і т. д.

Алгоритм головних компонентів

Крок 1. Нормалізація всіх пояснювальних змінних:

Крок 2. Обчислення кореляційної матриці

Крок 3. Знаходження характеристичних чисел матриці r з рівняння

,

де Е — одинична матриця розміром тхт.

Крок 4. Власні значення упорядковуються за абсолютним рівнем вкладу кожної головної компоненти до загальної дисперсії.

Крок 5. Обчислення власних векторів a_k розв'язуванням системи рівнянь

за таких умов:

Крок 6. Знаходження головних компонентів — векторів

Головні компоненти мають задовольняти умови:

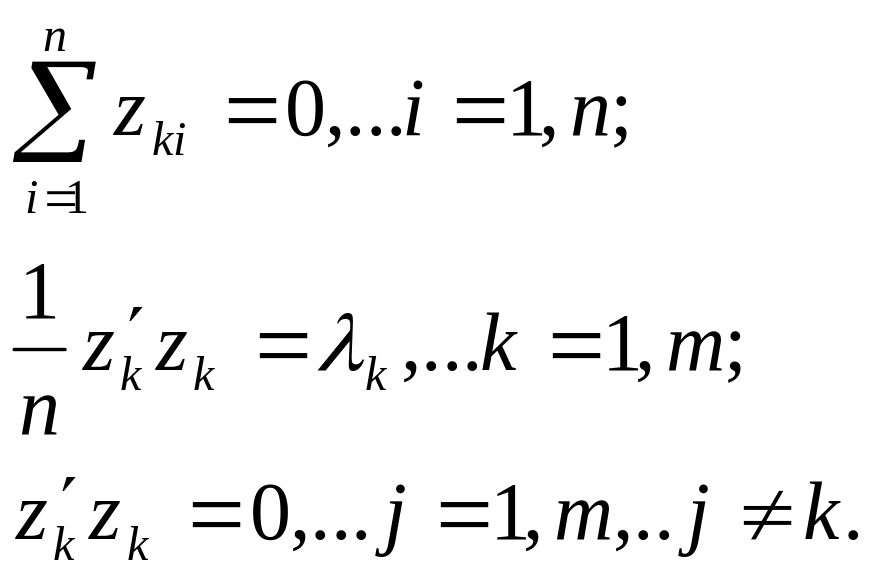
Крок 7. Визначення параметрів моделі :

Крок 8. Знаходження параметрів моделі :

87. Припущення, які були зроблені при оцінюванні параметрів моделі 1МНК, на практиці можуть порушуватися. Проблеми мультиколінеарності пов'язані з порушенням умови . Тепер розглянемо особливості економетричного моделювання, коли порушується умова , згідно з якою припускається, що відхилення мають такий розподіл імовірностей, який зберігається для всіх спостережень. Тоді дисперсія залишків лишається незмінною для кожного спостереження.

Означення 1. Якщо дисперсія залишків стала для кожного спостереження, тобто , то ця її властивість називається гомоскедастичністю. Часто у практичних дослідженнях явище гомоскедастичності порушується. Випробування на наявність чи відсутність гомоскедастичності звичайно не практикується, але здебільшого можна висунути гіпотези про правдоподібність альтернативних припущень щодо пропорційності помилки до X.

Означення 2. Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, тобто , то це явище називається гетердскедастичністю. Якщо існує гетероскедастичність залишків, то це спричинюється до того, що оцінки параметрів моделі 1МНК будуть незміщеними, обґрунтованими, але неефективними. При цьому формулу для стандартної помилки оцінки, строго кажучи, застосувати не можна. Гетероскедастичність призводить до порушення властивостей незміщеності та ефективності оцінок параметрів моделі, здобутих за допомогою 1МНК. Тому завжди постає потреба вивчати це явище і. якщо воно існує, для оцінювання параметрів моделі застосовувати узагальнений метод найменших квадратів (метод Ейткена).

88. Можливість перевірки припущень про наявність гетероскедастичності залежить від природи вихідних даних. Розглянемо методи перевірки гетероскедастичності для різних вихідних даних.