77. Оператор оцінювання 1мнк

Скористаємося моделлю (4.1), для якої виконуються умови (4.2)–(4.5), щоб оцінити параметри методом 1МНК.

Рівняння (4.1) подамо у вигляді: . Тоді суму квадратів залиш­ків u можна записати так:

Продиференціюємо цю умову за А і прирівняємо похідні до нуля:

або

(4.6)

Тут — матриця, транспонована до матриці незалежних змінних X.

Звідси

(4.7)

Рівняння (4.6) дає матричну форму запису системи нормальних рівнянь, а формула (4.7) показує, що значення вектора А є розв’язком системи таких рівнянь.

Формули (4.6) і (4.7) можна дістати й інакше.

Так, помноживши рівняння (4.1) зліва спочатку на , а потім на матрицю , дістанемо:

Оскільки то справджується рівність

.

Згідно з (4.4), коли , , отже,

(4.7)

Неважко показати, що оцінки Â, обчислені за (4.7), мінімізують суму квадратів залишків u. При цьому значення вектору Â є розв’язком так званої системи нормальних рівнянь

.

Якщо незалежні змінні в матриці X взяті як відхилення кожного значення від свого середнього, то матрицю називають матрицею моментів.

Числа, що розміщені на її головній діагоналі, характеризують величину дисперсій незалежних змінних, інші елементи відповідають взаємним коваріаціям.Отже, структура матриці моментів відбиває зв’язки між незалежними змінними. Чим ближчі показники коваріацій до величини дисперсій, тим ближчий визначник матриці до нуля і тим гірші оцінки параметрів . Далі буде показано, що стандартні помилки параметрів прямо пропорційні до значень, розміщених на головній діагоналі матриці .

. Оцінювання параметрів моделі методом найменших квадратів

Звернемося до прикладу простої економетричної моделі, де потрібно кількісно оцінити зв’язок між витратами на споживання та доходами сім’ї (див. підрозд. 2.3). Щоб оцінити параметри моделі (2.16), необхідно сформувати вихідну сукупність спостережень, кожна одиниця якої характери­зуватиметься витратами на споживання і доходами сімей. Припустимо, що економетрична модель споживання будується для тієї групи людей, в якій зі збільшенням доходів зростають витрати на споживання, тобто модель має вигляд (2.16).

Рис. 2.2. Кореляційне поле точок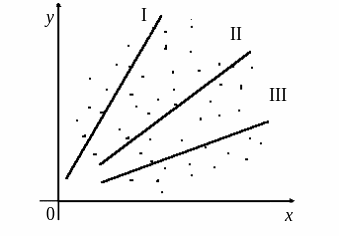

Зобразимо кожну пару спосте­режень у системі координат, де величина витрат на споживання відкладається на осі ординат, а доходів — на осі абцис. У результаті дістанемо кореляційне поле точок (рис. 2.2).

На підставі гіпотези про лінійність зв’язку між витратами на споживання і доходом сімей (див. рис.2.2), через кореляційне поле точок можна провести безліч прямих ліній, які різняться між собою параметрами і . Так, якщо витрати на споживання описуватимуться прямою I, то відхилення їх фактичних значень від розрахункових матимуть переважно знак «мінус». Якщо вони описуватимуться прямою III, то ці відхилення будуть переважно додатними, а якщо прямою II, то кількість від’ємних і додатних відхилень буде приблизно однаковою. Наявність серед відхилень переважно від’ємних чи додатних значень підтверджує, що вони мають невипадковий характер. А це означає: певна пряма лінія не адекватно описує фактичну залежність між витратами на споживання і доходом сімей. Звідси постає задача — застосувати метод найменших квадратів для оцінювання параметрів моделі, щоб відхилення фактичних витрат од розрахункових на основі прямої мали приблизно однакову суму від’ємних і додатних значень, а також були б найменшими. Останнє буде свідчити про те, що розрахункові значення витрат на споживання максимально наближені до фактичних, а це є гарантом вірогідності моделі.

Отже оцінки найменших квадратів такі, що лінія регресії проходить обов’язково через точку середніх значень ( , ), то оцінки параметрів моделі можна дістати так:

; ;

, .
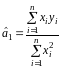