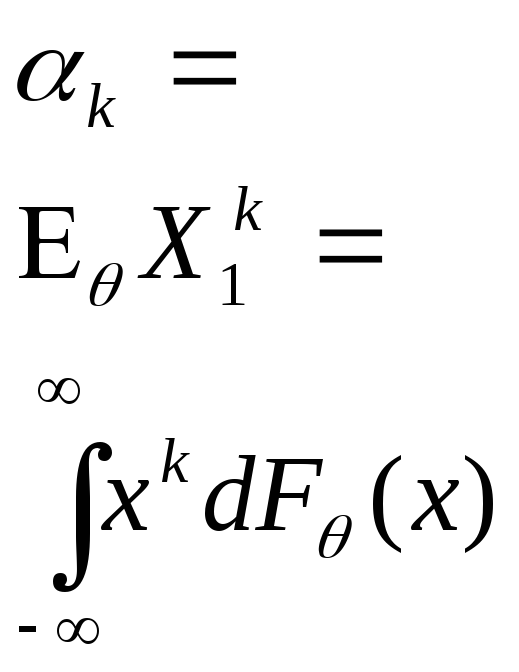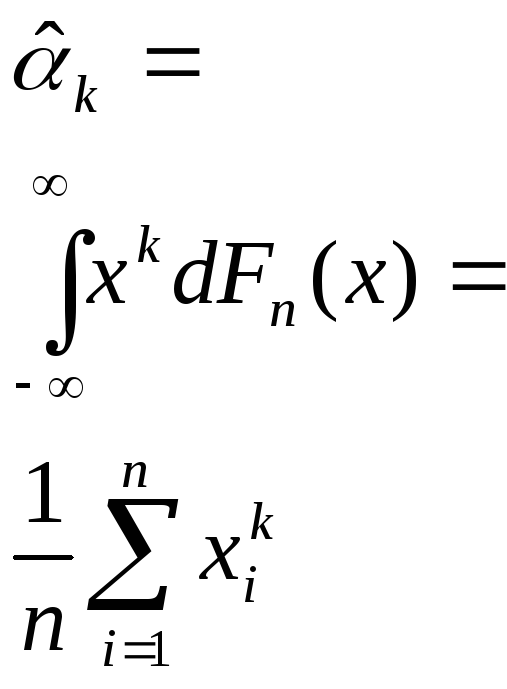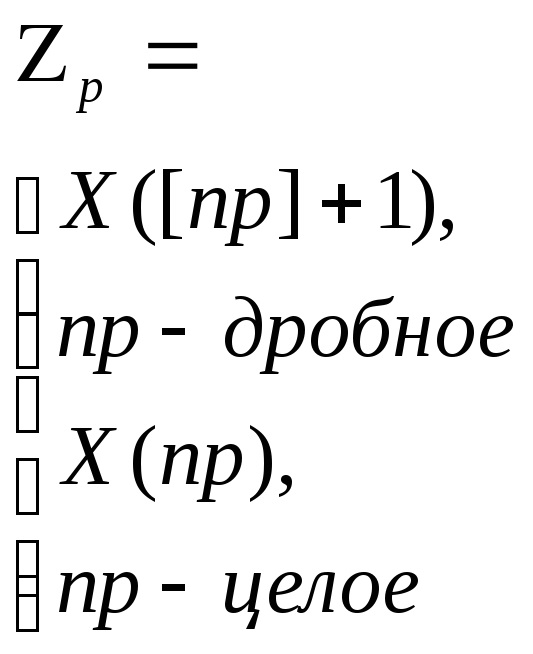Шпаргалка по статистике / Вопросы по ТВиМС [1-7]

1.Основные понятия математической статистики. Статистический эксперимент. Виды задач математической статистики.

Математическая статистика занимается составлением выводов об имеющихся данных (о модели эксперимента).

Базовое вероятностное пространство (Ω,₣,Ρ)

Частный случай – распределение случайного вектора:

Ω=Х=Rⁿ ; ₣=Д_n – борелевская σ-алгебра ; Ρ – распределение вероятностей

Получили более мелкое пространство, которое удобно использовать при работе с моделями математической статистики (Х, Д_n,Ρ).

Статистический эксперимент – тройка объектов (Х, Д_n,Ρ), где Ρ={Р_θ,θєΘ} - семейство вероятностей.

Стандартные предположения о семействе Ρ :

(1) Р_θ =Р_θ1 * Р_θ2 …*Р_θn , т.е. результат наблюдений (Х₁ … Х_n) є Rⁿ – независимые случайные величины при V θєΘ

(2) Р_θ1=Р_θ2=…=Р_θn , т.е. результат наблюдений (Х₁ … Х_n) є Rⁿ – независимые одинаково распределенные случайные величины (НОРСВ).

Если (1) и (2) выполнены, то (Х₁ … Х_n) – выборка – набор независимых одинаково распределенных наблюдений.

В задачу математической статистики входит только анализ данных и их интерпретация.

Выбор модели определяется характером полученных данных и не входит в задачу математической статистики. Семейство вероятностей Ρ определяется целью статистических исследований (априорной информацией), поэтому Ρ может быть параметризованно по-разному.

Пусть имеется совокупность результатов эксперимента (генеральная совокупность), тогда выборка – набор элементов однородной генеральной совокупности.

Задача математической статистики – сделать выводы о характере распределения генеральной совокупности по выборке. Роль генеральной совокупности в нашей модели играет теоретическое распределение.

Р_θ - теоретическое значение распределения, соответствует распределению генеральной совокупности.

Типы задач математической статистики:

1. Точное оценивание – по результатам наблюдений выбрать значение Р_θє Ρ , которое оптимальным образом согласуется с данными.

2. Интервальное оценивание - по результатам наблюдений выбрать область

Θ0 (Х₁ … Х_n) С Θ т.ч. при V θєΘ Р_θ(Θ0 (Х₁ … Х_n) э θ)≥1-α , где α - определенное маленькое число. Т.е. выбор такого множества, которое накрывает теоретическое значение параметра с вероятностью не меньше (1-α).

3. Проверка статистических гипотез – по результатам наблюдений выбрать из

Н₁… Н_n наиболее подходящую, где Н_i – взаимоисключающие гипотезы (предположения о значении параметров Н_i: θєΘ_i ; Θ_i∩Θ_i=0 ; UΘ_i=Θ).

2. Основные понятия. Статистики, оценки. Состоятельные, несмещенные, асимптотически нормальные оценки. Смещение оценки.

Пусть имеется (Х, Д_n,Ρ), где Ρ={Р_θ,θєΘ} - статистический эксперимент.

Статистика - V отображение из Х в какое-то пространство Е (T: Х->E)

Отображение δ: Х->Θ точечная оценка параметра Θ (δ(х) – оценка параметра).

δ(х) можно сделать зависящей от n определенным образом δ(х)= δ_n(х) sdfg

Оценка δ(х) (в смысле δ_n(х)) называется состоятельной, если δ_n(х)-> θ ; V θєΘ по вероятности, т.е. Р_θ(|δ_n(х) – θ|>ε)->0 при n->∞.

Оценка сильносостоятельная, если Р_θ(δ_n(х) –> θ(почти наверное))->1

Оценка δ(х) называется несмещенной, если Е_θδ(х)= θ и асимптотически несмещенной если Е_θδ_n(х)-> θ при n->∞.

Асимптотически нормальна, еслипо распределению

3. Выборочный метод. Эмпирическая функция распределения. Теорема Гливенко – Кантелли (план док-ва). Преобразование Смирнова. Теорема Колмогорова. Оценивание теоретической функции распределения эмпирической. Гистограмма и полигон частот.

Пусть (Х₁ … Х_n) выборка из распределения Р_θ . Истинное значение Р_θ - теоретическое распределение.

Эмпирическая функция распределения – функция следующего вида:

Fn(x) = 1/n*, где

Т.е. ее значение в точке х равно отношению числа наблюдений меньше х к общему числу наблюдений.

Теорема (Гливенко – Кантелли)

Пусть(Х₁ … Х_n) выборка из распределения с ф.р. F,тогда sup|Fn(x)-F(x)| почти наверное->0

План док-ва:

доказывается сходимость на ограниченном интервале (т.к. F неубывает и ограничена). Показывается, что изменение между двумя соседними точками мало. Доказывается, что сходимость на концах следует из :

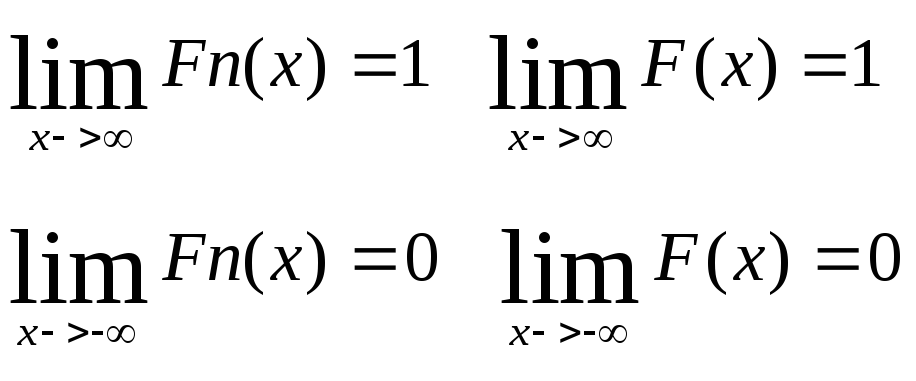
-> sup|Fn(x)-F(x)|->0

Преобразование Смирнова

Пусть Х случайная величина с ф.р. F (непрерывна),тогда F(x)=Y-новая с.в. имеющая равномерное распределение U(0,1), т.е.:

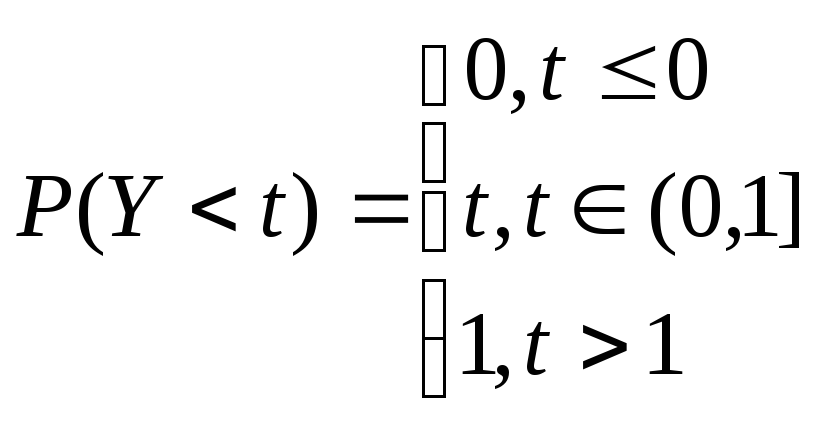
Если F строго возрастает, то :

Теорема Колмогорова

Пусть (Х₁ … Х_n) выборка из распределения F(непрер.),тогда , где К – распр-е Колмогорова, т.е.:

, где

С ростом n, эмпирическая ф.р. приближается к теоретической. У э.ф.р. имеется -окрестность, по т. Гливенко – Кантелли вероятность того, что истинная ф.р. лежит в этой эмпирической -окрестности ->1 при .

По т. Колмогорова, вероятность того, что истинная ф.р. лежит в - окрестности эмпирической стремится к пределу K(), где К(х) – ф.р. Колмогорова.

Пусть >0 – маленькое число, F – истинная ф.р., тогда если F₀=F , где F₀ предполагаемая ф.р., то с вероятностью

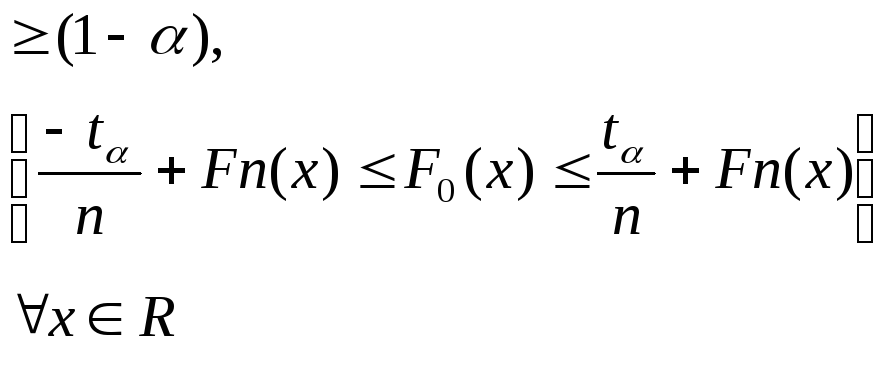
, т.е.

- доверительный интервал для теоретической ф.р.

Гистограмма и полигон частот:

Один из способов наглядного представления статистических данных – Гистограмма частот. Область значений с.в. разбивается на равные интервалы, подсчитывается число значений с.в. попавших в интервал и на каждом интервале строится прямоугольник, с основанием на этот интервал и высотой V/(nh), где V – число выборочных точек попавших в этот интервал, n – объем выборки, h – длина интервала. Площадь каждого такого прямоугольника по т Бернулли будет сходится при n->к вероятности попадания с.в. в интервал.

Для оценки гладких плотностей используют методику, основанную на полигоне частот – ломаной кривой, строящейся следующим образом: если построена гистограмма частот, то ординаты ее средних точек на каждом из интервалов последовательно соединяются отрезками прямых. Гистограмма и полигон – статистические аналоги теоретической плотности.

4. Вариационный ряд и его характеристики. Примеры. Понятие рангов. Одномерные и совместные распределения элементов вариационного ряда в абсолютно непрерывном случае.

Пусть (Х1…Хn) – наблюдения, определим порядковые статистики Х(i): - те же значения, упорядоченные по неубыванию, и ранги R1…Rn, где Ri – порядковый номер i-го элемента в ряду порядковых статистик.

- вариационный ряд.

По наблюдениям всегда можно составить вариационный ряд, но если есть совпадающие наблюдения, то ранги м.б. определены неоднозначно.

По вариационному ряду нельзя восстановить наблюдения, т.к. неизвестен порядок, но их можно восстановить по вариационному ряду и рангу.

Под распределением в математической статистике подразумевают соответствие между наблюдаемыми вариантами и их частотами.

Предположим, что (Х1…Хn) – выборка из абсолютно непрерывного распределения L, а F(x) и f(x)=F’(x) – функция и плотность наблюдаемой величины, тогда:

дифференцируя равенство по х, выделяя первое слагаемое при m=k получаем что плотность имеет вид:

совместная плотность распределения:

5. Выборочные характеристики распределений. Пример(моменты, квантили). Характеристики 1-го и 2-го типа. Теорема о сходимости выборочных характеристик к теоретическим (план док-ва).

Пусть : F->R (R^d) – числовая характеристика распределения, т.е. F₀F – множество всех ф.р. (F), где F F₀ – значение числовой характеристики.

Выборочный аналог числовой характеристики (F) - (Fn) (выборочная числовая характеристика )

Примеры:

	Теоретическое	Выборочное
Мат. ожидание
Дисперсия
Момент к-го порядка
Квантиль порядка р () (точка пересечения функции распределения и уровня р)

Выборочные характеристики бывают 2х типов:

1-й тип: Выборочные характеристики моментного типа вида:

, где Н – непрерывная функция от к-аргументов, а G – известные функции.

2-й тип: Непрерывные функционалы от F

- непрерывная ф-я от F, в смысле

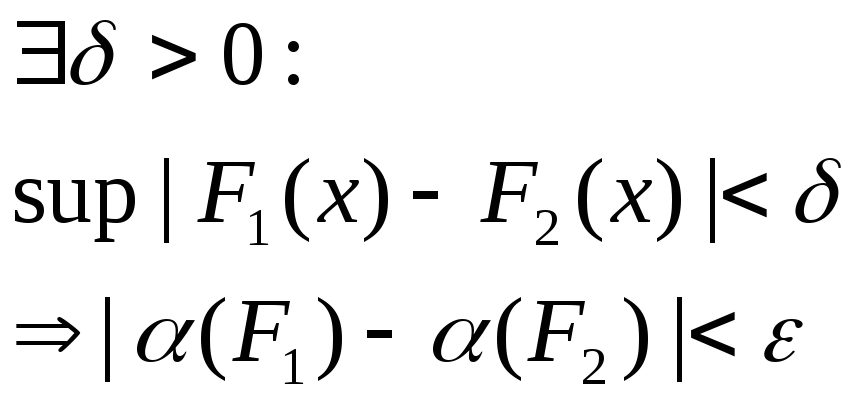
Теорема:

Пусть - характеристика 1^го или 2^го типа, тогда , F – теорет.ф.р.

1й тип

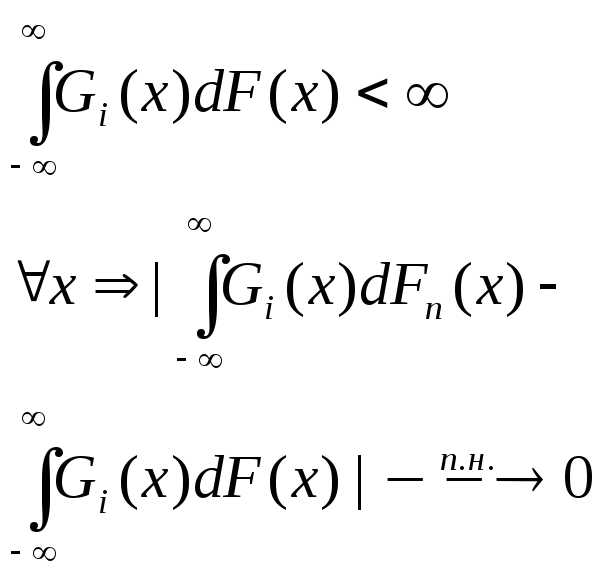
согласно З.Б.Ч.

где и

т.к. Н – непрерывна, то сходится и при всех I, тогда для любой сходящейся последовательности:

F-непрер. <=> для любого a_n->x F(a_n)->F(x)

Поэтому:

2й тип согласно т. Гливенко – Кантелли sup|Fn(x)-F(x)|->0 откуда в силу непрерывности α => α(Fn)-> α(F).

6. Асимптотическая нормальность выборочных квантилей. Теорема.

Теорема:

Пусть (X1..Xn) – выборка из абсолютно непрерывного распределения с плотностью f, ξ_p – теоретическое значение квантили порядка р и f(ξ_p)>0 и f(ξ_p)=F’(ξ_p), т.е. F дифференцируема в ξ_p, тогда:

Док-во:

Пусть , тогда

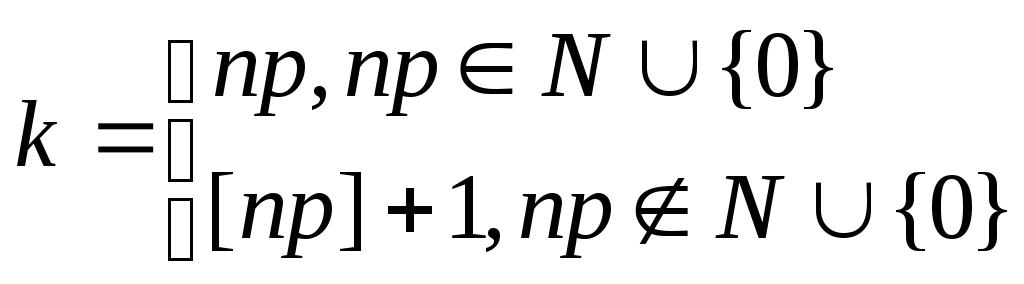
Пусть , тогда событие

Y₁…Y_n – НОРСВ => - НОРСВ имеющая распределение Бернулли с плотностью

Е=а D=a(1-a)

Согласно Ц.П.Т. :

7. Некоторые распределения, использующиеся в мат.статистике. Нормальное распределение, гамма распределение, хи – квадрат распределение.

1) Нормальное распределение

~N(X – абсолютно непрер. и

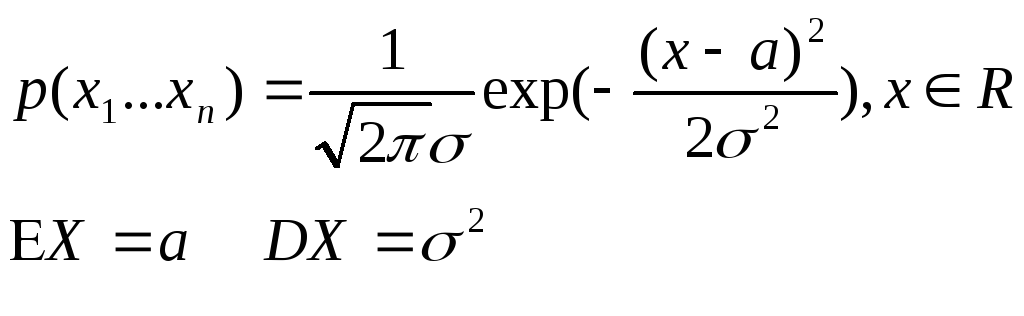
Многомерное нормальное

Стандартное нормальное с плотностью соответствует n независимых нормальных величин с N(0,1).

Нормальное общего вида: Пусть - стандартного вида, тогда Y= имеет нормальное распределение общего вида.

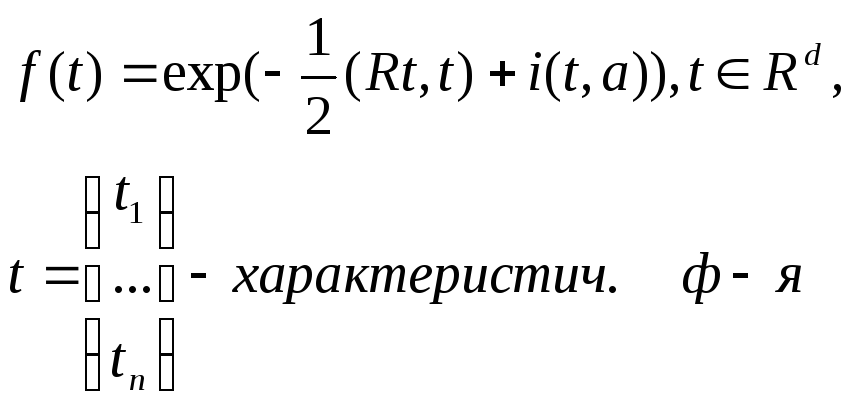
где - вектор мат. ожиданий, R – матрица ковариации.

~ N(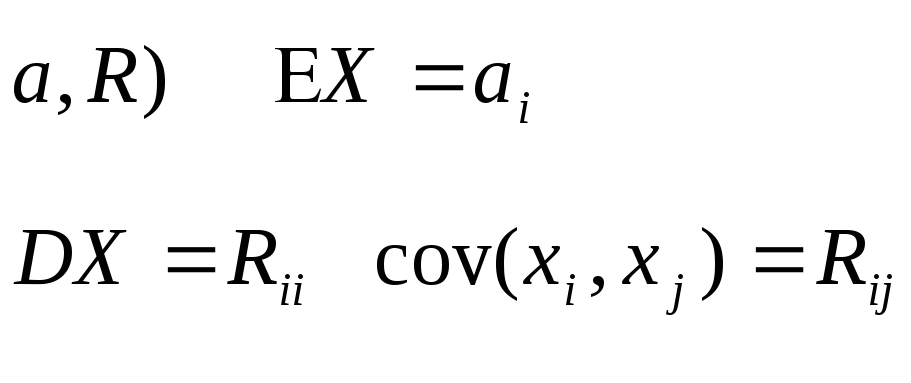

если |R|, то - абсолютно непрерывный, причем:

2) Гамма распределение Г() – абсолютно непрер-е с плотностью

, где -гамма функция

Свойства:

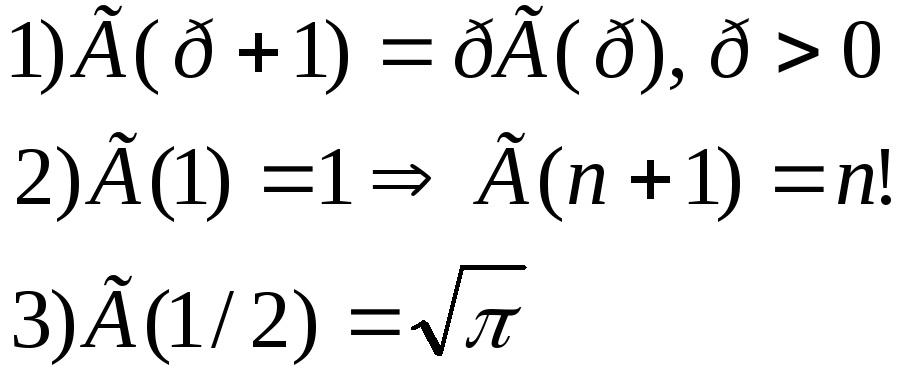
Частные случаи гамма распределения:

1) ~Exp(α)

2) ~N(0,1), тогда ~Г(1/2,1/2)

Свойства Г-распределения:

1) характ-ая функция

2)Если X~ Г() и Y~ Г() X и Y независимы, то X+Y ~ Г()

3) хи-квадрат распределение

- хи-квадрат с n степенями свободы если