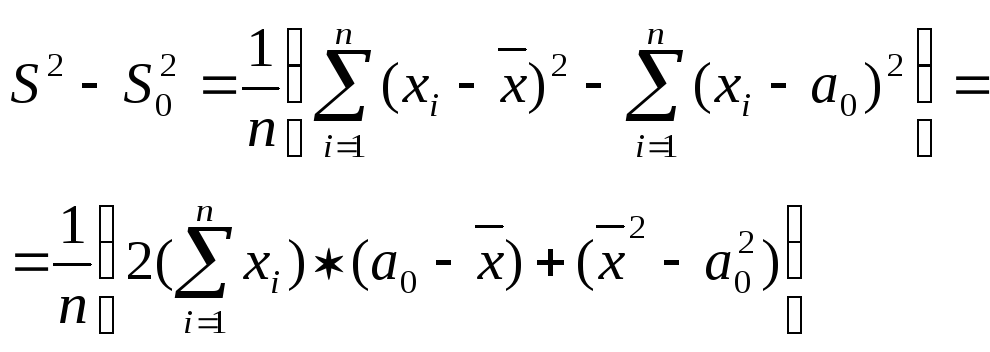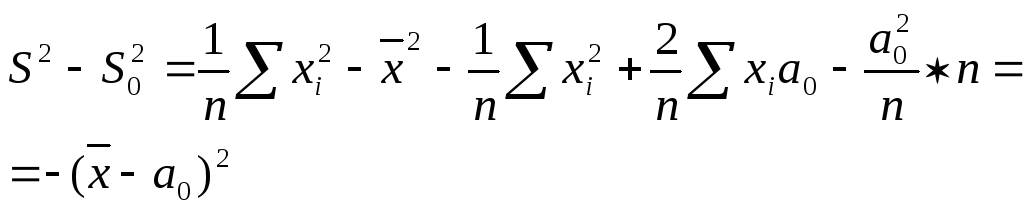Шпаргалка по статистике / Вопросы по ТВиМС (32-38]
.doc32 Другие методы построения доверительных интервалов. Построение доверительного интервала для параметра распределения Бернулли.
Пусть Т-статистика,![]() –
ф.р.
–
ф.р.
![]()
Пусть
![]() уровень
знач.
уровень
знач.
![]()
Пусть F- непр.
Рассм. ур-ние
![]()
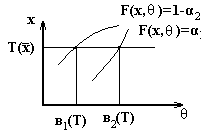
F
– монот. возр. попар.![]()
Подставляем сюда статистику Т и рассм. сечение этой области на уровне Т. Получаем в1 и в2
![]() дов. инт. ур. α.
дов. инт. ур. α.
Пусть
![]() ,
т.е
,
т.е
![]()
![]() ,
т.е
,
т.е
![]()
Утверждение:
![]() монотонно зависит от параметра
монотонно зависит от параметра
θ х.Тогда![]() -доверительный интервал уровня α.
-доверительный интервал уровня α.
Док-во:

Замечание: Свойство монотонной зависимости от параметра по распределению обладают большинство разумных оценок параметра.
? как вычислить FT
Отметим, что данное свойство можно использовать и в дискретном случае (точное равенство м.б. не получиться)
в1,в2 – т.ч.
Дискретный случай:

![]()
![]()
тогда [в1(Т),в2(Т)] – д. и. ур. α
Пример: (распределение Бернулли)
x1…xn – выборка из Bi (1,θ)
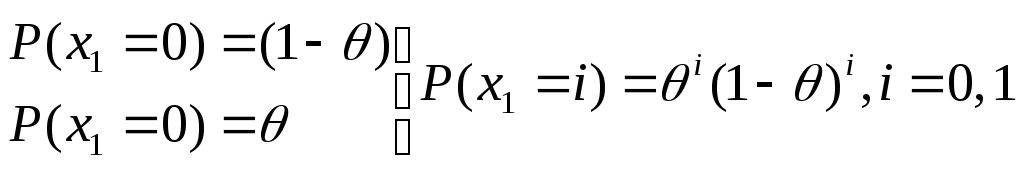
![]()
![]()
![]()
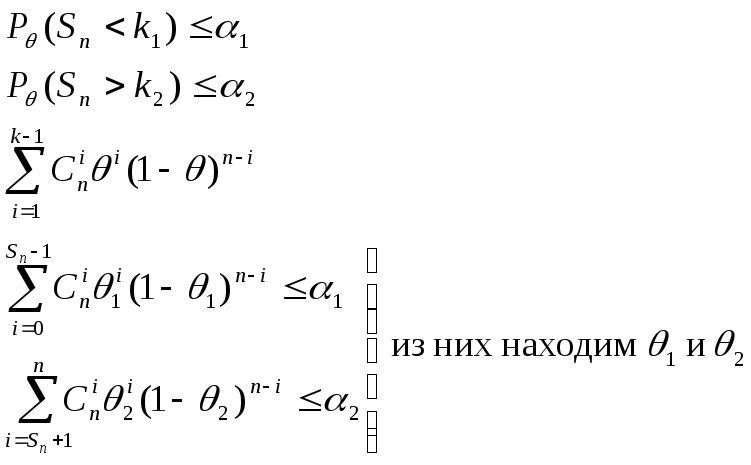
убывают пар-ры
![]()
Иногда можно
отказаться от условия, что распр. G(T;θ)
– не зависит от параметра, если можно
вычислить
![]()
(т.е.
I2)
тогда
![]() - доверит. мн-ва ур-ня α.
- доверит. мн-ва ур-ня α.
33. Асимптотические доверительные интервалы. Построение асимптотических доверительных итервалов на базе асимптотически нормальной оценки параметра. Пример (распределение Бернулли, три подхода и связь между ними).
Определение: Послед-ть областей
![]() -
ас.д.область уровня α для θ,
-
ас.д.область уровня α для θ,
если
![]()
Если
![]() -
ас.д.и.
-
ас.д.и.
Замечание:
если
![]() - ас.д.и.ур.α
- ас.д.и.ур.α
Способ построения:
Найти
![]() ,
т.ч.
,
т.ч.
а)
![]()
б)
![]()
Построение ас.д.и. на базе ас.норм.оценки
Пусть δ –
ас.норм.оценки, т.е.
![]()
т.е.
![]()
Пусть
![]()
![]()
![]()
Если удастся
выразить θ из
![]()
то находим д.и. в противном случае
Пусть δк(θ) – состоят. оценка для δ(θ)
(δ(θ)0) тогда

Пример: (распр. Бернулли)
x1…x2 – выборка из Bi (1,θ)

-------------------------------------------------------------------------
Интегральная теорема Муавра-Лапласа(ИТМЛ):
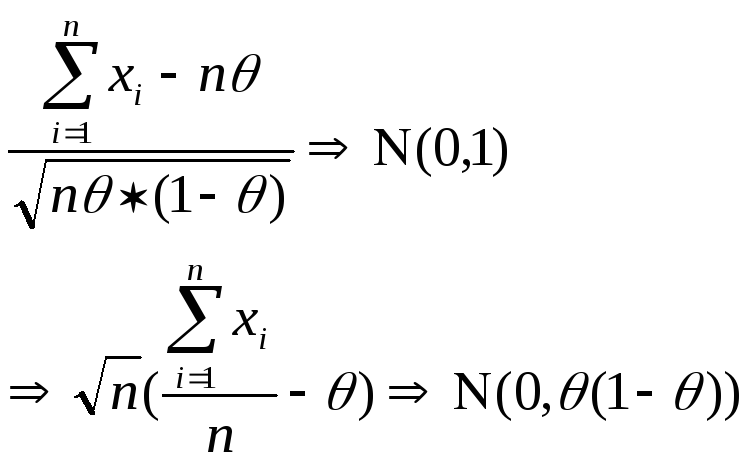
-------------------------------------------------------------------------
Итак
![]()
![]()
Находим х2. Решаем:

![]()
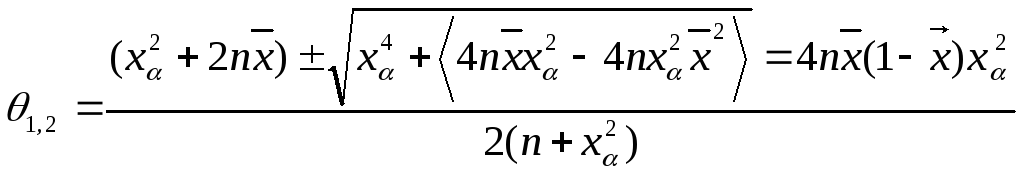
АДИ (асимпт, доверит, интервал)
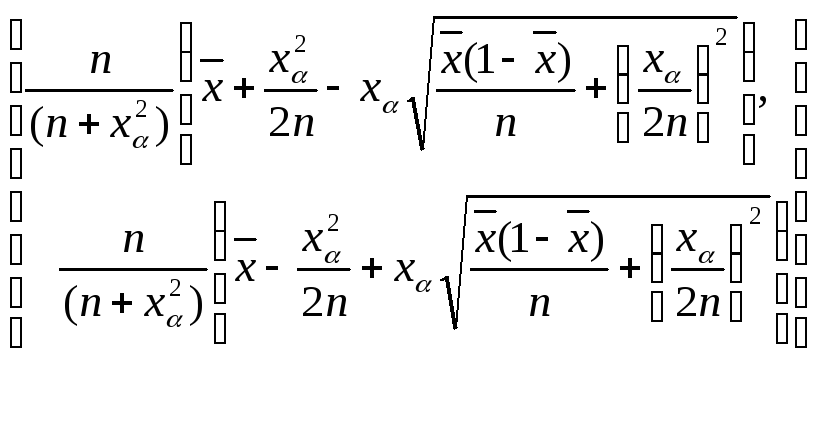
б) Вернемся
![]()
![]() -
сост. оценка для
-
сост. оценка для
![]()
Пусть
![]()
Решаем
![]()

![]()
в)
![]()
![]()
![]() тогда АДИ
тогда АДИ
![]()
34. Постановка задачи проверки статистических гипотез. Понятие статистической гипотезы, вероятностей ошибок 1-го и 2-го рода, критерия, доверительной, критической области и области сомнений, мощности критерия. Выражение вероятностей ошибок в терминах критерия.
Статистическая гипотеза
Гипотеза – утверждение
![]()
Опред: Стат. гипотеза – утверждение о значении пар-ра θ.
Стат. гипотеза
м.б. записана в виде
![]()
Опред: стат.
гипотеза простая,
если
![]() - одноточечное.
- одноточечное.
В прот. случае стат. гип. – сложная
Задача: Выдвигается
основная гип.
![]() и альтернативная (несколько)
и альтернативная (несколько)
![]()
По результатам наблюдений надо выбрать Н0 или Н1
Правило выбора – критерий.
Опред: Критерий
![]()
Значение
![]() вероятность
отвергнуть осн. гипотезу по результатам
наблюдений
вероятность
отвергнуть осн. гипотезу по результатам
наблюдений
![]()
Согласно критерию
область
![]() разбивается на 3 части:
разбивается на 3 части:
|
Доверит.
|
Обл.
сомнений
|
Критическая
область
|
Опред: Критерий - нерандомизированный, если (Х)={0,1}(или Рθ((Х) (0,1))=0 θ)
В противном случае
![]()
- рандомизированный.
- рандомизированный.
Классический подход Пирсона
В результате решения задачи ПСГ могут возникнуть следующие ситуации
|
|
Принять Н0 |
Принять Н1 |
|
Верна Н0 |
+ (верное реш.) |
ошибка 1 рода |
|
Верна Н1 |
ошибка 2 рода |
+ |
Ошибка 1 рода наиболее нежелательна. Вероятность ошибки 1 рода д.б. ограниченна некоторым числом α. α – уровень значимости критерия.
Рθ(ош.
1 рода)
α,
θΘ0
, Рθ(ош.
1 рода)=![]()
Ошибка 2 рода:
Р(ош. 2 рода)=![]()
![]() -
мощность критерия
-
мощность критерия
Задача: Найти
критерий ,
такой что

если эта задача имеет решение *, то *-равномерно наиболее мощный (РНМ) критерий
РНМ критерий не всегда существует.
35. Задача проверки простой гипотезы при простой альтернативе. Лемма Неймана-Пирсона. Примеры наиболее мощных критериев.
Пусть Н0: θ=θ0 – простая гипотеза. Рассмотрим задачу проверки Н0 при альтернативе:
Н1: θ=θ1 - простая (т.е. Θ={θ0,θ1}). Замечание: Поскольку альт. – простая, то РАМ критерий, если называть Н.М. Пусть
μ – мера доминирующая
сем.
![]()
Например:
![]() ;
(μ – мера Лебега или считающая мера,
если возможно) Функция правдоподобия:
;
(μ – мера Лебега или считающая мера,
если возможно) Функция правдоподобия:
![]()
Введем статистику
отношения правдоподобия:
![]()
Замечание: 1) Не зависит от выбора доминирующей меры
2) Если
![]() =0
или
=0
или
![]() =,
то выбор очевиден.
=,
то выбор очевиден.
Лемма Неймана-Пирсона
В задаче проверки Н0: θ=θ0 при альтернативе Н1: θ=θ1, существует наиболее мощный критерий уровня значимости α, он строится следующим образом:
 р[0,1)
р[0,1)
Причем С выбирается следующим образом:
![]()
Замечание: 1) Если
![]() >0,
то р выбирается однозначно и
>0,
то р выбирается однозначно и
![]()
2) Если
![]() =0
не важно значение р – критерий не
рандомизированный.
=0
не важно значение р – критерий не
рандомизированный.
Дополнение:
Критерий
определяется однозначно на множестве
![]()
Если критерий есть функция от МДС, то он есть и единственный.
Доказательство: Перепишем критерий в виде:
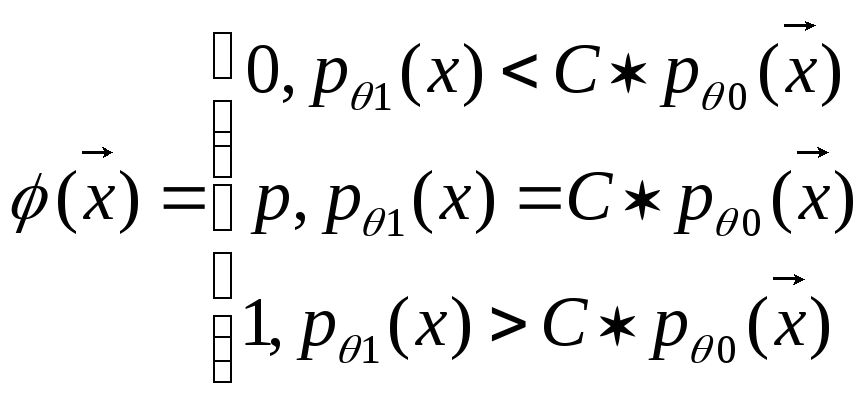
Пусть имеется другой критерий, у которого тот же уровень значимости,
т.е.
![]()
![]()
![]() =
=
=![]() |*С и вычтем из
|*С и вычтем из
В свою очередь мощность критерия:

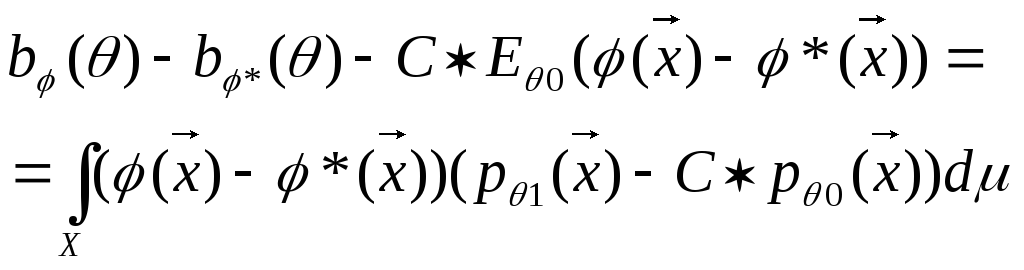
![]()
![]()

Дополнение: Можно показать, что на S+ и S- Н. М. критерий определяется однозначно с
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
36. Наиболее мощный критерий для проверки односторонней гипотезы. Пример (проверка качества воды)
Пусть
![]() - статистика, причем функция правдоподобия
выражается как функция от этой статистики.
- статистика, причем функция правдоподобия
выражается как функция от этой статистики.
а)
![]()
б)
![]() -
монот. Ф-я Т при
-
монот. Ф-я Т при
фиксир.
![]()
(либо возр. либо
убыв. ![]() )
)
Поставим задачу проверки одностор. Гипотезы
![]() ,
при альтернативе :
,
при альтернативе :
![]()
(пусть
![]() монот.
возр. при
монот.
возр. при
![]() )
)
Теорема: РНМ критерий уровня α проверки Н0
при альтернативе Н1 вида

При этом константы
р и С находятся из соотношения:
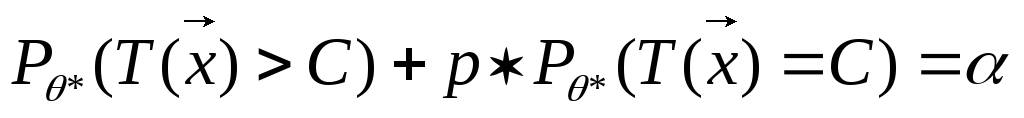
Док-во:
1)Найти
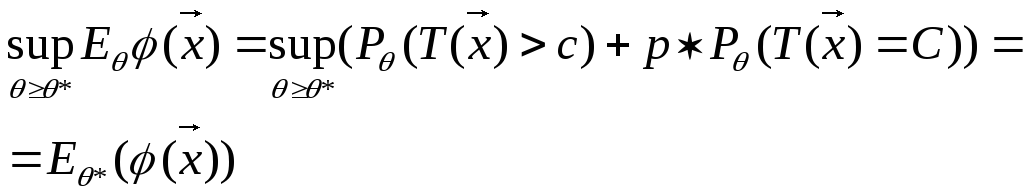
это критерий уровня α
это критерий уровня α
2)
![]()
Рθ(ош.
1 –го рода) =
![]()
Мощ-ть:
![]()
Пусть
![]()
![]()
![]()
если
- Н.М. критерий, то
![]()
![]()
![]()
![]()
![]()
2. - Н.М. критерий проверки
![]()
![]() , θ
РНМ
, θ
РНМ
Пример: Требуется, чтобы концентрация бактерий в жидком растворе не превышала 1 бактерия на единицу объема
(![]() S/ед.V)
S/ед.V)
Проводится след. стат. эксперимент:
Отбирается n
проб объема V=1.
Эти пробы помещ. в среду благоприятн.
для роста бактерий. Если проба заражена,
то раствор мутнеет. К- число зараженных
проб. Проверить гипотезу ![]()
Решение:
V=N*v
![]() -
бактерий в этом объеме. Вероятность
попадания бактерий в соотв. маленький
объем, не зависимо от других = 1/N
-
бактерий в этом объеме. Вероятность
попадания бактерий в соотв. маленький
объем, не зависимо от других = 1/N
При фиксир. N
рассмотрим
![]() -
число бактерий в объеме
-
число бактерий в объеме
v–
имеет распределение Бернулли
![]()
![]()
Единственное, что наблюдается, есть ли бактерии в объеме.
Р(проба чистая)=
![]() - распред. Бернулли
- распред. Бернулли
Если V>>v, то можно считать что отбор проб прошел независимо
Получили, что х1…хп – выборка из р. Бернулли
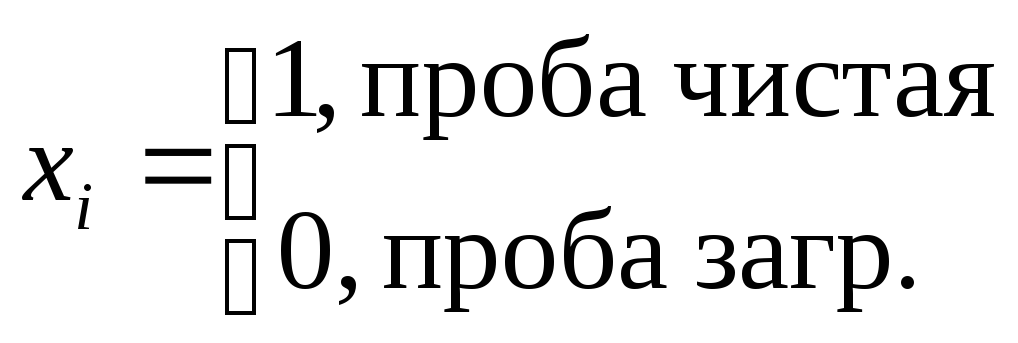
![]() - число зараженных
проб
- число зараженных
проб
![]()
Будем строить НМ – критерий
![]()
![]()
 ,
,
![]()
Если мало чист. проб – отвергаем гипотезу, если много - принимаем
![]()
![]()
![]()
Если С>n, то вероятность =1
Воспользуемся интегральной теоремой Муавре-Лапласа.
Ас. критерий при больших n
 (Т.к.
(Т.к.
![]() )
)
![]()
![]()
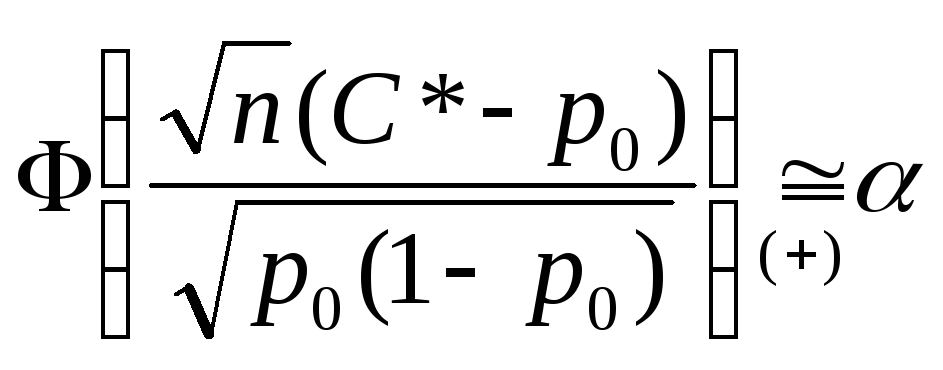 ,
,![]() ,
С*=
,
С*=![]() - находим из (+)
- находим из (+)
37. Использование отношения правдоподобия при проверке сложной гипотезы в параметрической задаче с мешающим параметром.
38. Понятие асимптотического критерия
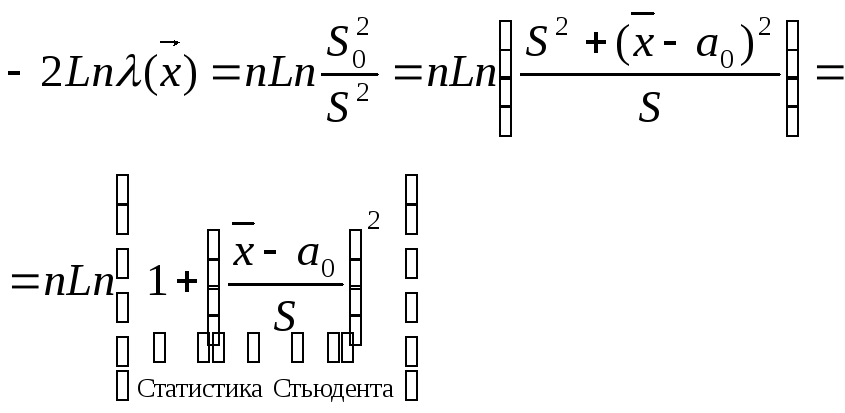
Пусть
![]()
![]()
При опред. условиях регулярности

Величина
![]()
Пример: х1…хn – выборка из N(a,2)
H0: a=a0
H1: aa0
Функция правдоподобия
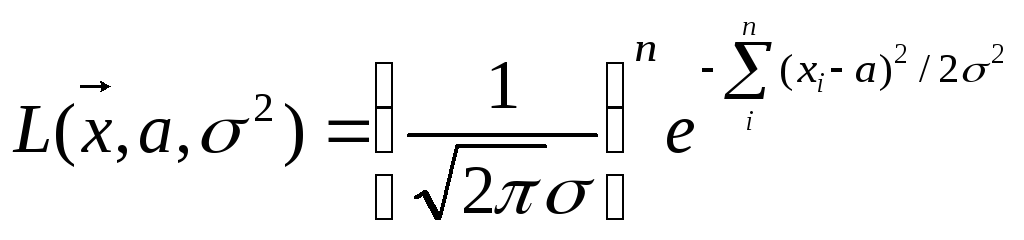
![]()
![]()
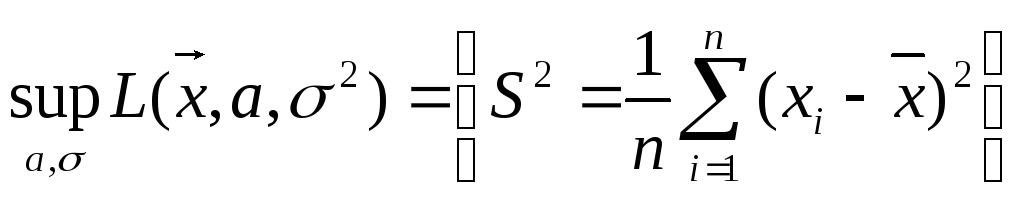 =
=![]()
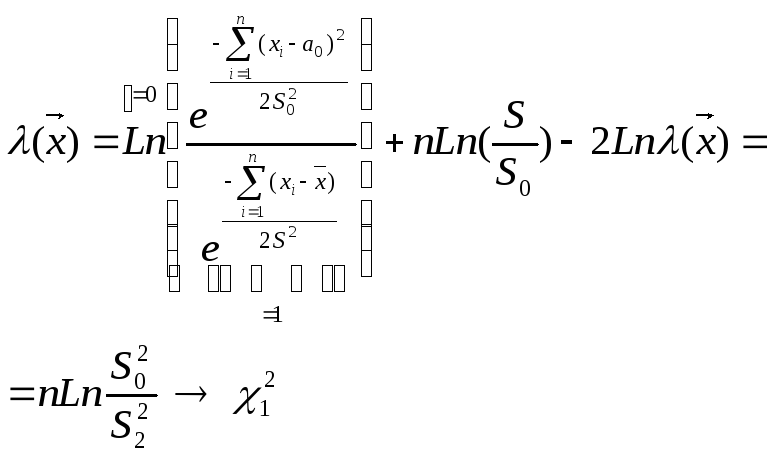
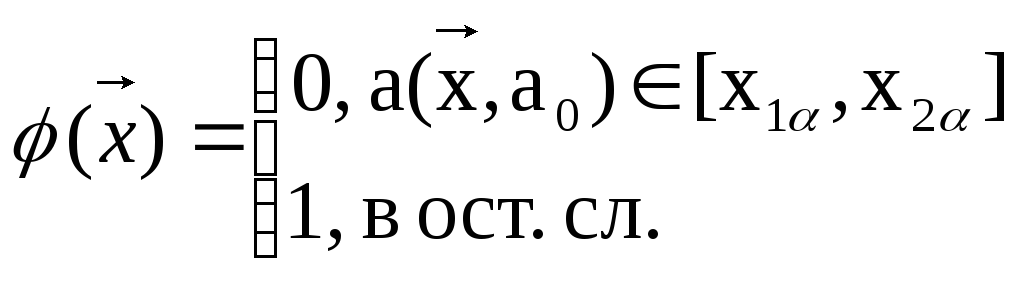
ас. кр. ур. α, [x1α, x2α] – квантиль