Шпаргалка по статистике / Вопросы по ТВиМС [26-31]

Неравенство Рао-Крамера. Эффективные по Фишеру оценки.

Пусть X_1…X_n – выборка из P ={P_θ: θ є ĤR} – семейство однопараметрическое, мера доминирующая семейство P: >> P с плотностями P_θ. Условие регулярности:

эксперимент (семейство) называется регулярным если:

1. P_θ непрерывно дифференцируема по

2. В условиях семейства допускается дифференцирование под знаком интеграла.

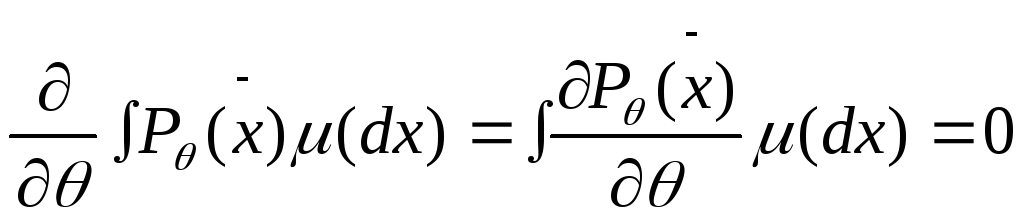
3. I() : I() (0,)

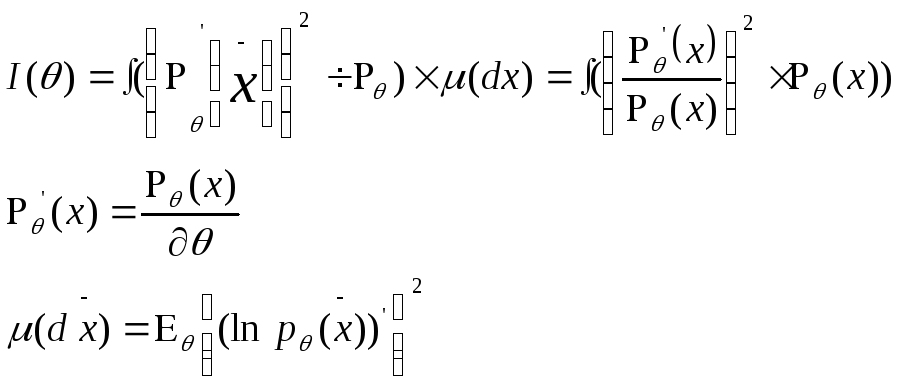
- функция правдоподобия

- информация Фишера (характеризует, насколько сильно различаются плотности возле точки параметра ).

С ростом количества наблюдений информация накапливается.

Свойства информации.

Теорема: Пусть имеются 2 независимых экспиремента:

P₁ ={P_1θ, θ є Ĥ} P₂ ={P_2θ, θ є Ĥ}

Рассмотрим экспиремент:

- т.е. 2 независимых эксперимента

Пусть оба они регулярны : и

Тогда эксперимент общий тоже регулярный, а

Док-во: Пусть исходные семейства были регулярны, тогда по св1 регулярности ρ₁ и ρ₂ , следовательно

Следовательно свойство 1 выполнено для ρ.

Свойство 2: Рассмотрим

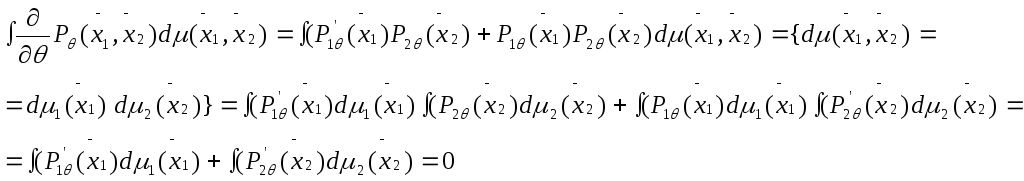
Свойство 3: {сложение информации}Замечание: В условиях регулярного эксперимента ( log L =0

Неравенство Рао-Крамера (теорема).

Оценка δ – разрешенная, если .

{диф-ние под знаком интеграла}

Пусть - регулярный эксперимент, причем - информация Фишера и

- разрешенная оценка, b() = - -смещение оценки . Тогда и +

-дает нижнюю границу для оценки (нер-во Крамера)

Следствие: Если - несмещенная, то

Док-во: Отметим . Поскольку - разрешенная

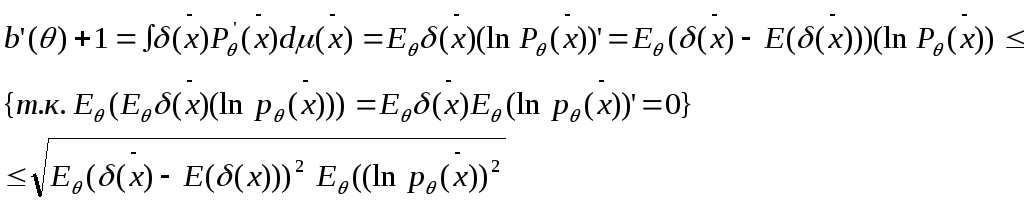
1-е нер-во.

Т.к.

Значение информации в знаменателе характеризует информацию в исх. данных для того, чтобы оценить параметр

Когда бывает равенство в нер-ве Рао-Крамера?

Рав-во достигается в том и только в том случае

(*)

1. Рав-во Коши-Бун-ко, когда (*) пропорц-но x - const но зависит от парам-ра, принимает разные значения

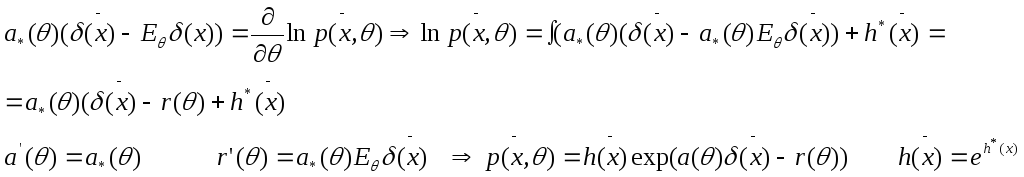(**) - однопараметрич. экспотенциальное семейство

Т.е. рав-во возможно в случае экспотенц. сем-ва

2. Из (**) берем

3. Пусть эксперимент регулярен и 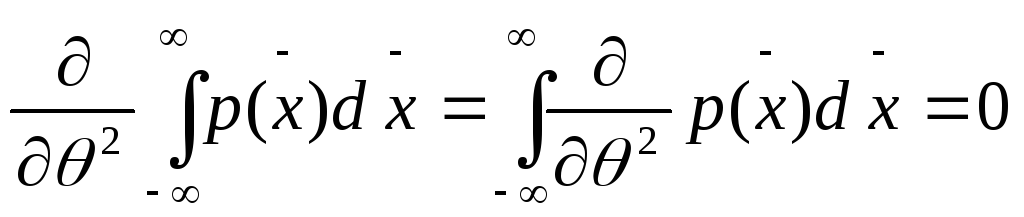; если это условие выполнено, тогда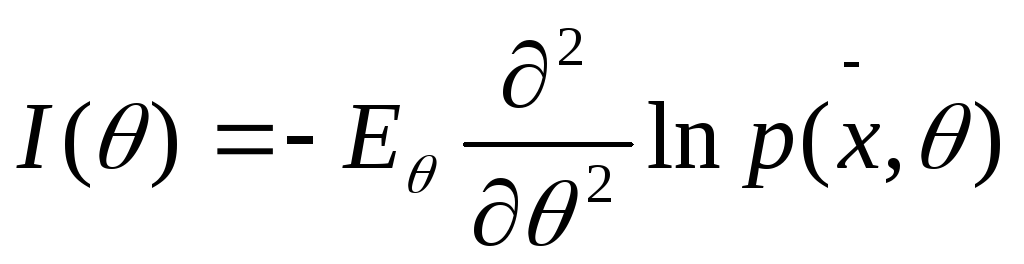. Покажем

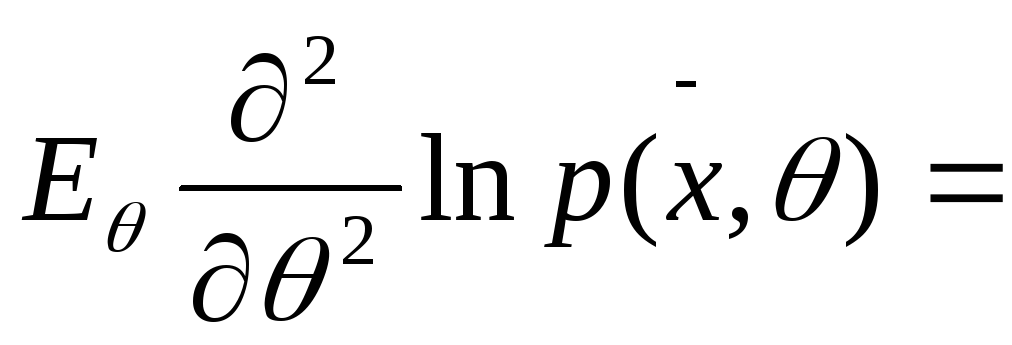
Оценка называется эффективной по Фишеру, если

a) - несмещенная {только в эксп.семействах}

b) -только для правельных пар-ров

Примеры вычисления информации и примеры эффективных оценок. Эффективность и метод максимального правдоподобия.

1. Пусть Х₁…Х_n ~ N(a,)

a) - известно. Вычислим информацию об а.

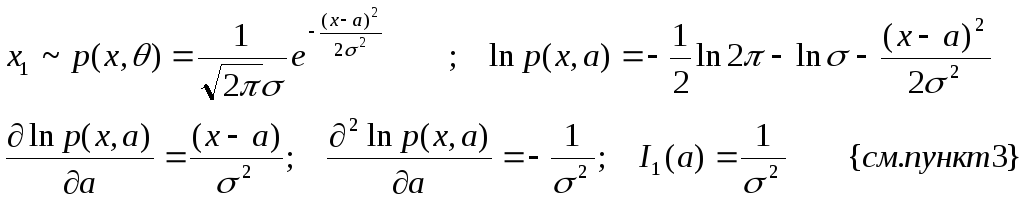
Информацию по всему эксперименту: I(a) = инфо. складывается (n незав.экспериментов) =

б) а – известно; ;

Пуассона:

Гамма:

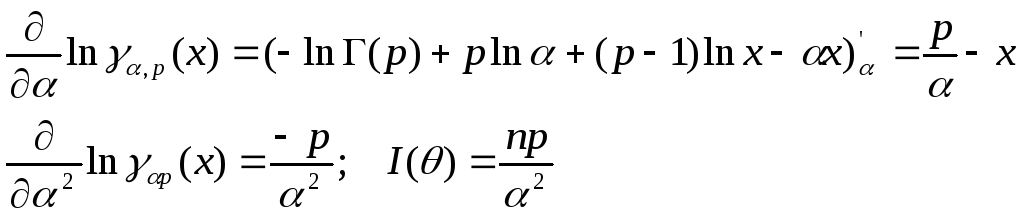
Об эффективности: Х₁…Х_n ~ N(a,), - извест., ; - R-эффективна

б) а – известна;

{инфо о регулярных экспериментах}

Теорема: Пусть - R-эф.оценка для. Тогда - ОМП.

Док-во: Оценка R-эффективна - нек.функция. Если оценка R- эф., то при возведении в квадрат получим:

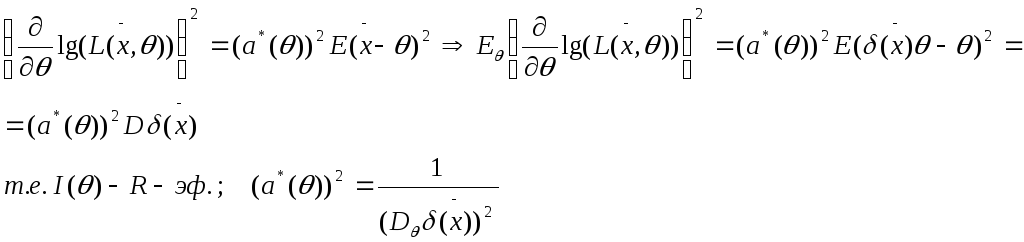
Асимптотически нормальные оценки. Асимптотическая эффективность по Фишеру. Пример (сравнение асимптотической эффективности двух оценок среднего по выборке из нормального распределения).

Эксперимент регулярный. (X, F, P) Рассмотрим асимп.нормальную оценку , т.е.

, где - последовательность оценок =

Будем говорить, что оценка асимптотически эффективна по Фишеру, если

{предельная дисперсия}. 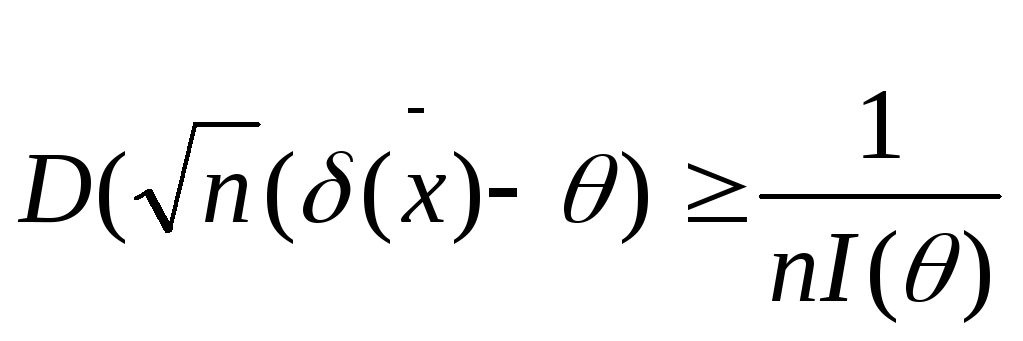для несм.

- наилучшая оценка в асимпт.смысле – дисперсия.

Замечание об ОМП: Пусть эксперимент регулярен, дважды дифференцируем:

- ограничена ф-цией H(x)

. Тогда ОМП существует и 1) она состоятельна: ; 2) {сх-ть по распределению}

т.е асимптотически эффективна

Пример: Пусть х₁…х_n~N(a,), - известна;

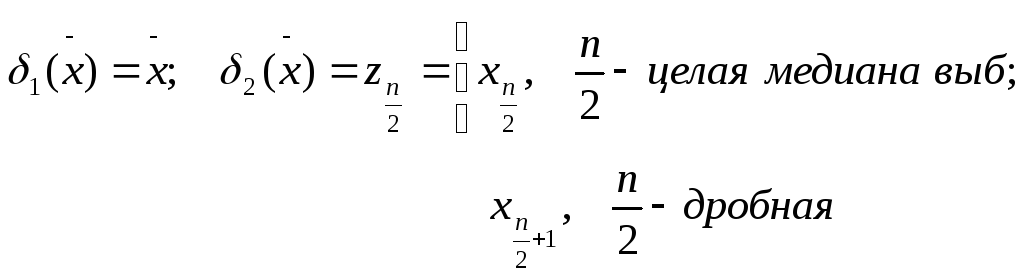
ЗБЧ: - независимо от а

Сверхэффективность. Пример Ходжеса. Робастные оценки.

Теорема об асимптотич. поведения выборки:

Квантили ; ;

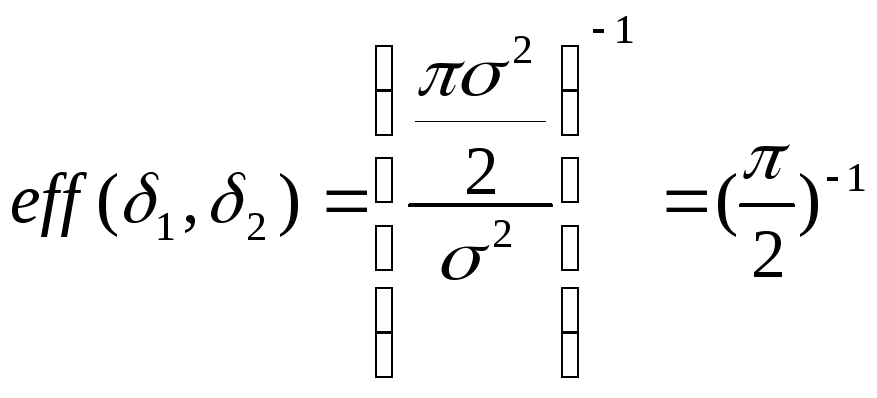- относительная эф-ть; по отн. к

Пример: Пусть

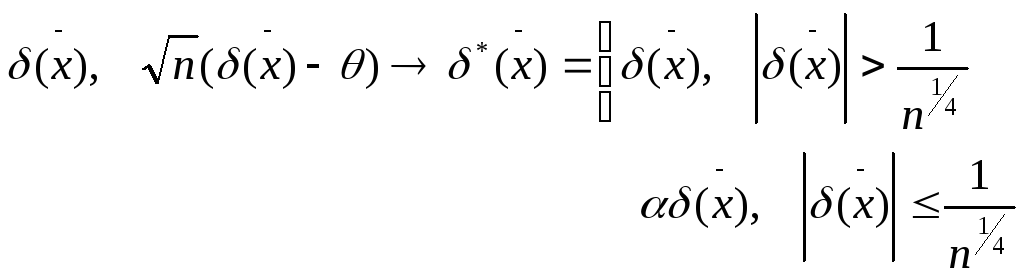
- фиксир. число

(*) (**)

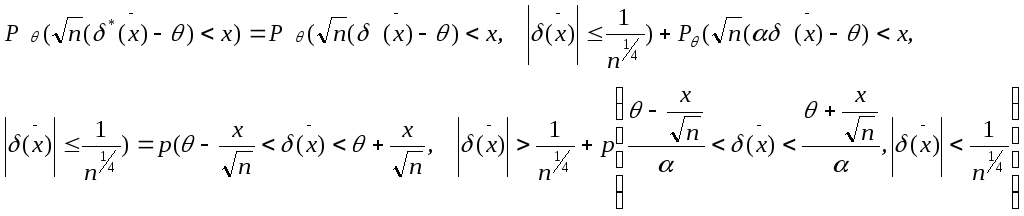- фиксированное число, - ас. норм. оценка

При , при достаточно больших n * ** (при достаточно больших n)

При * (= с какого-то момента). При достаточно больших n ** =

= при =0

при достаточно больших n =

= при достаточно

маленьком ; Дисперсия может быть сколь угодно мала.

=Явление называется сверхэффективность

Вывод: Можно построить оценку в отдельной точке параметрического множества, которая имеет сколь угодно высокую асимптотическую эффективность только в одной единственной точке.

Робастые оценки.

Чистая модель: (сем-во ; Загрязнения ;

Считается, что теоретическое распределение имеет вид

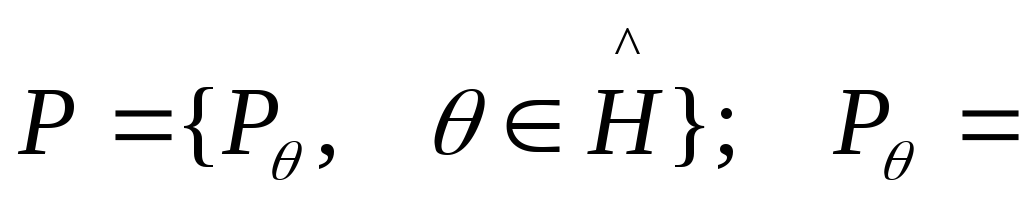
=; т.е. смесь распределений или выпуклая комбинация

- близко к 1; (1-) – спетень загрязнения

Робастая оценка – оценка, имеющая достаточную эффективность в чистой модели и эффективность которой мало зависит от загрязнения

Пример: для нормального распредения N(a, ) при загрязнении распределением Коши : C(a,b); для нормального N(a, ) – оптимальна, в смеш. модели – не состоятельна. Более робастой оценки: (выборочной медианы ) или

{суммируется только средняя часть}

Постановка задачи доверительного оценивания. Простейший метод построения доверительных интервалов (без примеров).

До сих пор мы говорили о точечном оценивании параметров. Будем строить множество: пусть 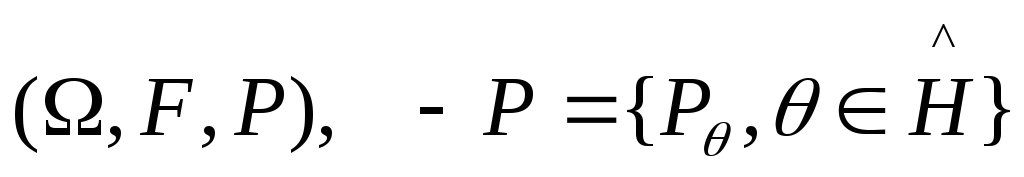- статистический эксперимент. Доверительной оценкой параметра уровня значимости (или 1ровня доверия ) называется статистика Ĥ: , где С –некоторая совокупность подмножества Ĥ,

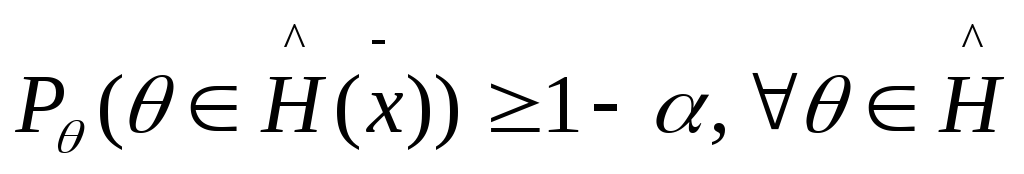; мн-во, построенное по результатам наблюдений, кот. с вероятностью накрывает истинное значение параметра

Замечание: необходимо накладывать какое-либо ограничение на множество С. Пусть (одномерный параметр), С – совокупность интервалов

. В этом случае доверительная оценка - доверительный интервал.

Альтернативное определение: Доверительный интервал уровня значимости наз-ся пара статистик T₁, T₂ : ; .

Основные методы построения ДИ. Пусть удается найти функцию

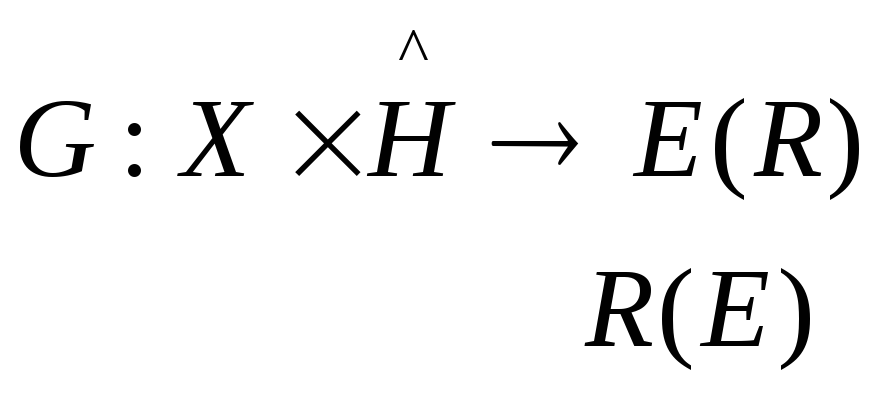
а) Распределение не зависит от параметра

б) ,тогда - интервал

в) Распределение - известно, т.е. можно найти

Примеры построения доверительных интервалов для параметров нормального закона (случай одной и двух выборок).

Пример: Нормальное распределение. Пусть х₁…х_n – выборка из N(a,) распределения. Построить ДИ для а, если - неизв. Выберем , не зависящую от второго параметра.

Решение: . По лемме Фишера имеет распределение Стьюдента: . Выберем : (используя таблицу,

Находим . Т.о.

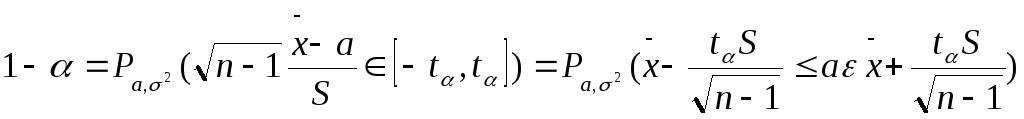
S-выб.дисперсия. ДИ

2. Строим ДИ для (а – неизв); по п.3 лемме Фишера:

. Очевидно, что , может быть выбраны неоднозначно. Решение Х² {рисунок}

Длина ДИ характеризует точность оценки. В случае Стьюдента построенный доверительный интервал кратчайший. Для - более сложная задача, поэтому находят ДИ из условий ; . Решение задачи . {Если нет априорной информации, нужно брать 2-сторонний интервал, если есть – односторонний}

4. Пусть - независимые. - неизвестна (мешающий параметр). Построим ДИ для a-b. Согласно лемме Фишера:

Т.о.

По лемме Фишера п.3

ДИ: 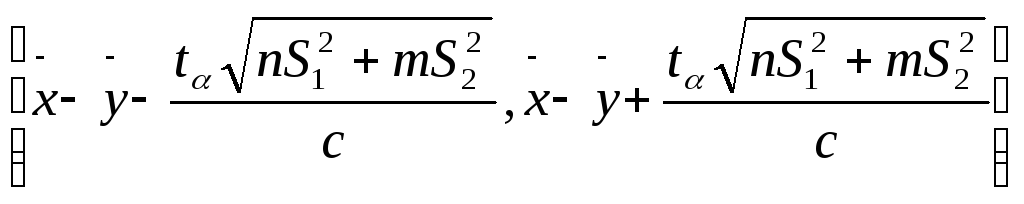для параметра (a-b) {считается что задано}

Построим ДИ.

4. ДИ для

П.3 леммы Фишера : ; По замечанию к лемме Фишера получим 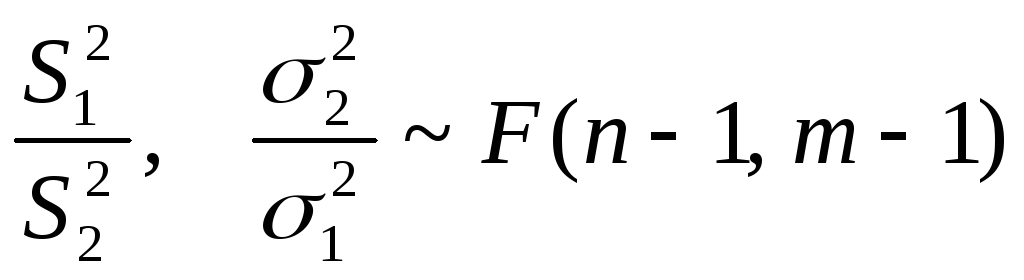- распределение Снедекора

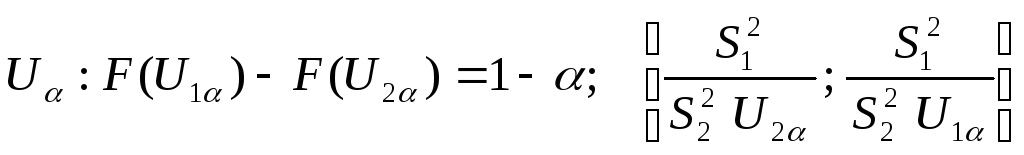- ДИ для

Примечание к примеру 3: мешающий параметр - одномерный, если , т.е. могут быть разные, т.е. мешающий – двумерный, то задача не решена, проблема Беренса-Фишера

{рисунок}

Доверительная оценка Ĥ называется состоятельной, если она стягивается в точку.

Если Ĥ- ДИ, то состоятельность равносильна тому, что .

В примерах 1-4 ДИ – состоятельные (т.к. в нормальных законах)

Пример5: Пусть x₁…x_n – выборка из ; - функция распределения х_1. Пусть при фиксиров. х – монотонная функция от . Тогда в качестве . Отметим ; , где - функция распределения