15. Теорема Лемана. Минимаксность выборочного среднего, как оценки мат. ожидания нормального распределения.

Теорема.

Пусть - последовательность байесовских оценок по отношению к априорным распределениям {Q_k} соответственно;

Если

Тогда - минимаксна.

Док-во

Оценка называется минимаксной, если она минимизирует максимальный риск, т.е.

:

Пусть - произвольная оценка. Тогда, поскольку Q_k – вероятностная мера и поскольку - байесовская:

Переходим к пределу

- минимаксна.

Пример.

Пусть Х₁ ,…,Х_n – выборка из N(,) c известным и надо оценить .

Предположим, что параметр имеет нормальное расперделение: ~ N(0,k), kN

Получаем последовательность байесовских оценок:

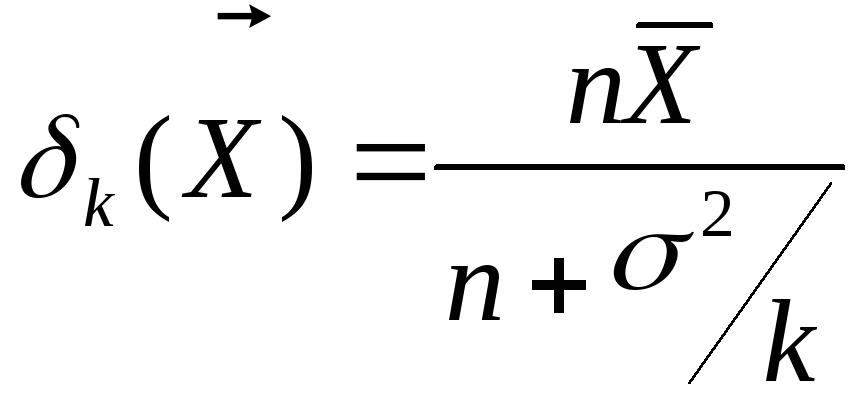
и соответствующую последовательность байесовских рисков:

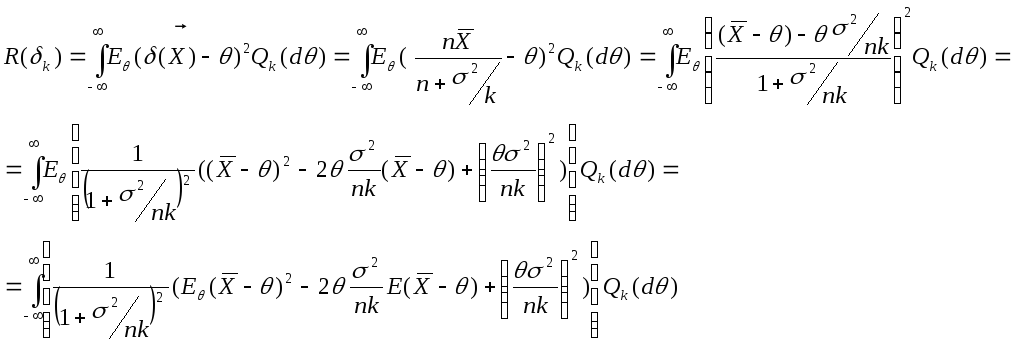
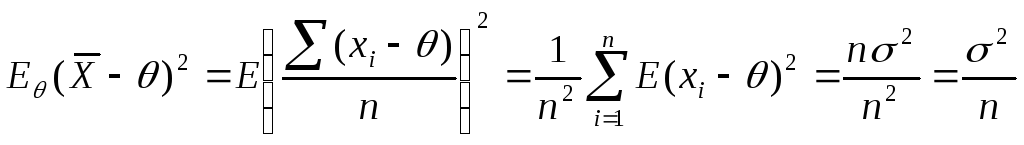
, где

,

т.е.

-оценка

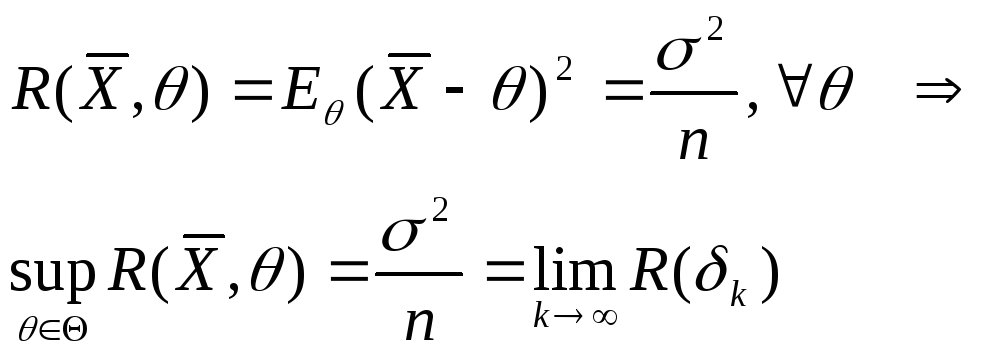
- минимаксна

16.Метод моментов построения статистических оценок. Примеры.

Пусть Х₁,…,Х_n –выборка из распеределения с начальными r моментами i порядка:

Они являются функциями от неизвестных параметров .

Начальные выборочные моменты i порядка.

Тогда метод моменов состоит в приравнивании выборочных и теоретических моментов одного порядка:

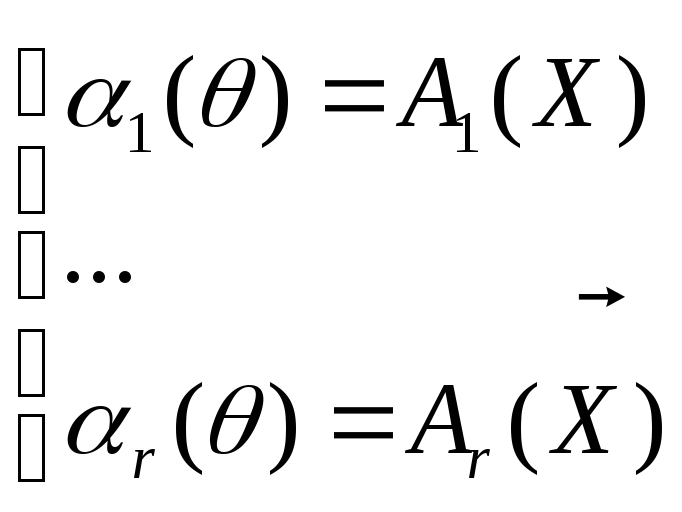, где r – выбирается сообразно тому, сколько нбх уравнений для существования и единственности решения,

обычно

Примеры.

1) распределение Бернулли

- теоретич. момент

- выборочный момент

Уравнение методом моментов:

- оценка методом моментов (ММ)

2) распределение Лапласа DE(a,b)

теор. момент 1 порядка

теор момент 2 порядка

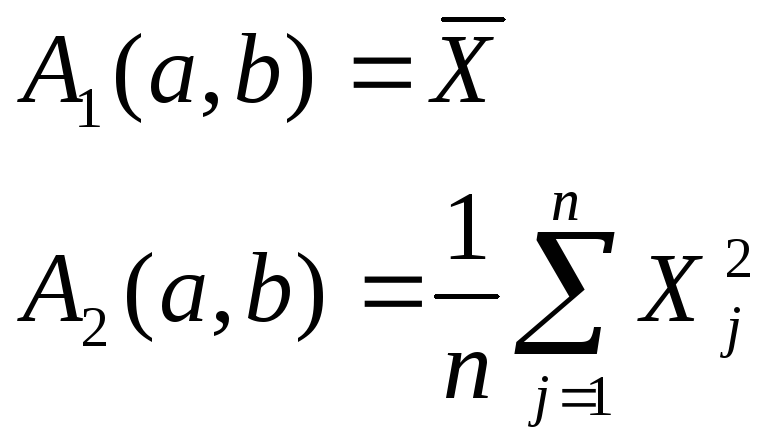выбор. моменты 1 и 2 порядка

Уравнение ММ:

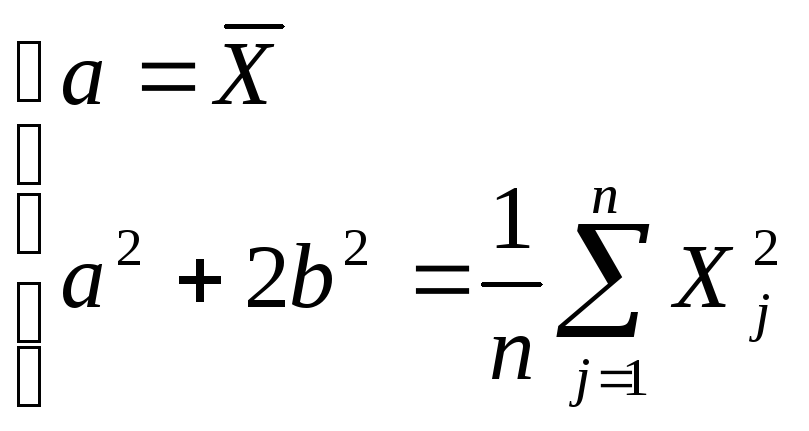
Оценки ММ:

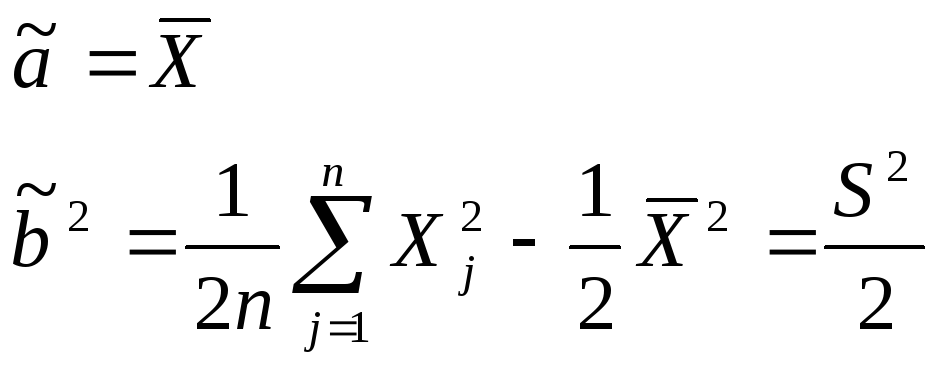
17.Метод максимального правдоподобия. Примеры.

Понятие правдоподобия позволяет сравнивать вероятносные шансы тех или иных исходов эксперимента при различных значениях параметра .

В рез-те эксперимента поступает более точная информация, тогда прикаждом фикс. Значении естественно сравнивать достоверности исходов через значение плотности ( или производной Радона-Никодима) относительно некоторой домин. меры.

Пусть - семейство вероятностных мер, доминирующих некоторой мерой .

(если величины имеют абс. непрер. распределение, то мера Лебега,

если дискретное – можно выбрать считающую меру на мн-ве возможных значений результата эксперимента)

- плотность распределения.

Функция правдоподобия является плотностью распределения случайного вектора :

Опр-е

Оценка - называется оценкой правдоподобия, если для каждого из выборочного пространства

Пусть Х₁,…,Х_n - выборка из одномерного семейства <<

- плотность

Выбираем , т.е.

и

функция правдоподобия

Идея метода макс. правдоподобия состоит в отыскании значения , максимизирующее правдоподобие, т.е.

В силу монотонности логарифма задача сводиться к максимизации логарифма правдоподобия.

И далее нахождения max:

Примеры.

1) распределение Бернулли

Х₁,…,Х_n ~ Bi(1,p)

- считающая мера на Z

Функция правд-я

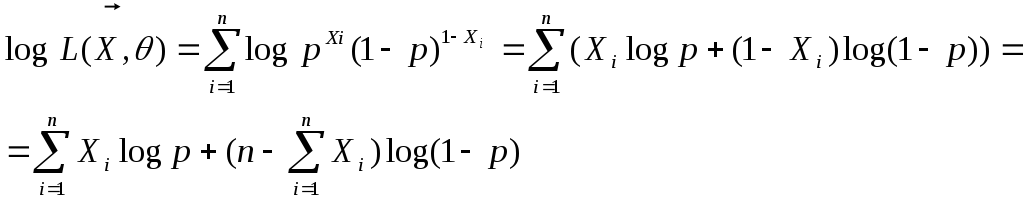
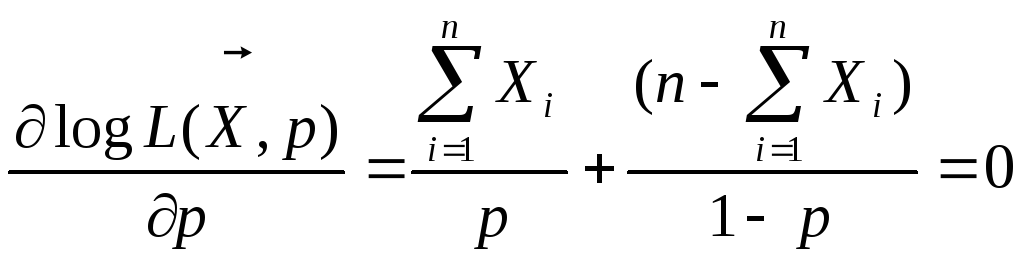
- оценка макс. правдоподобия

2)нормальное распределение

Х₁,…,Х_n ~ N(a,b),

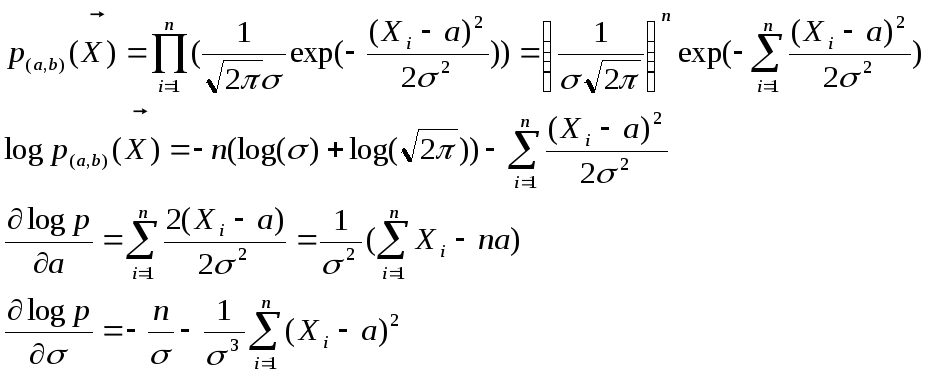
решаем уравнение

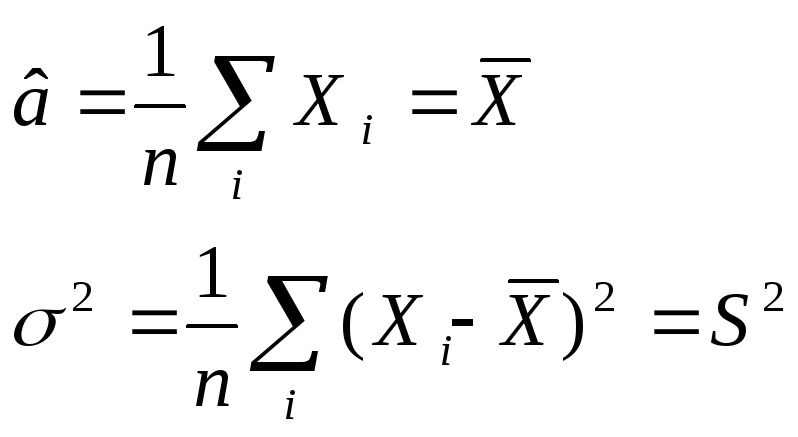
- ОМП

18.Достаточные статистики. Примеры.

Пусть (P), где - статистический эксперимент.

Т()- статистика. Статистика Т называется достаточной для семейства Р, если условное распределение вектора при условии Т не зависит от значения параметра , т.е

Знание того, где находиться на поверхности , не несет никакой дополнительной информации о теоретическом распределении, а следовательно, вся информация об исходном распределении содержится в Т().

Примеры.

1) Х₁,…, Х_n – выборка из функции распределения F, а F- любая функция распределения.

Можно показать, что НОРВС набор порядковых статистик в этом семействе

(х₍₁₎, …,х_(n)) – достаточная статистика.

Действительно,

Пусть , , тогда

Если перестановки i₁,…,i_n:

(окружить х_i таким множеством, что в нем только t_j и нет других)

(для домин. семейств это следует из определения)

2) Х₁,…, Х_n -выборка из распределения Бернулли, т.е.

(последовательность испытаний Бернулли)

Покажем, что - достаточная статистика

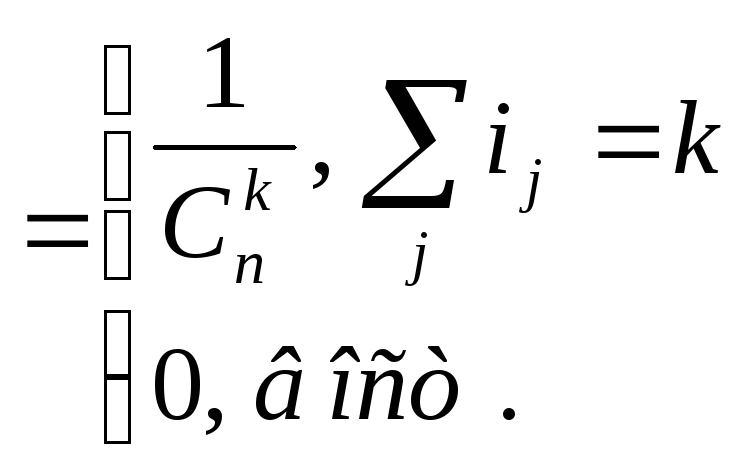не зависит от пар-ра - достаточная статистика для сем-ва распр-я Бернулли

20.Теорема факторизации Неймана-Фишера.

Лемма Хэлмоша-Сэвиджа

-конечна, то

такой, что Р доминируется линейной комбинацией :

Теорема

Р<<, -конечна

Для того чтобы статистика Т()была достаточной для , необходимо и достаточно, чтобы функция правдоподобия имела вид:

Док-во

а) не зависит от

, где

- плотность относительно меры

- плотность относительно меры

т.к. - доминирование мерой существует плотность по т.Радона-Никодима

в дальнейшем покажем: ,

б)Докажем, что

?

Т- измер. случ.величина

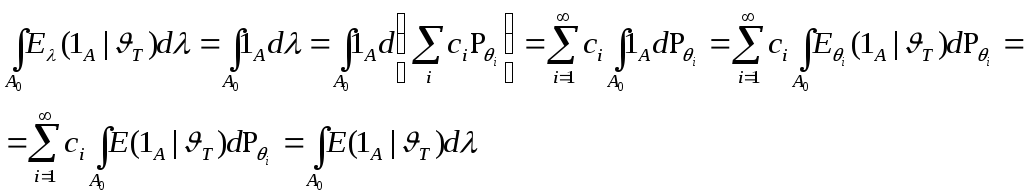
в силу единств. усл. мат. ожид. мы получаем:

в)рассмотрим сужение

тогда , (если на большой доминированна, то на маленькой и тем более)

(мы ее так опред)

Покажем, что на всякой сигма-алгебре F

Для этого надо показать, что

(известно, что )

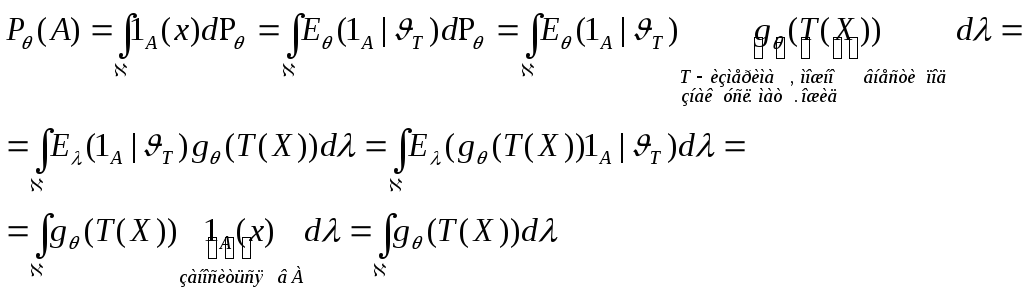
тогда по теореме Радона-Никодимаполучаем (единст-ть):

на F

возвращаясь к началу, мы получаем

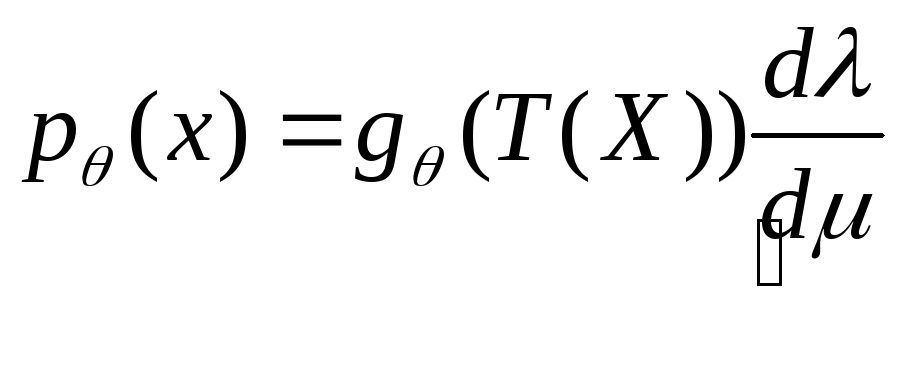
не зависит от

доказали в одну сторону

Обратное утверждение:

Пусть

т.е.

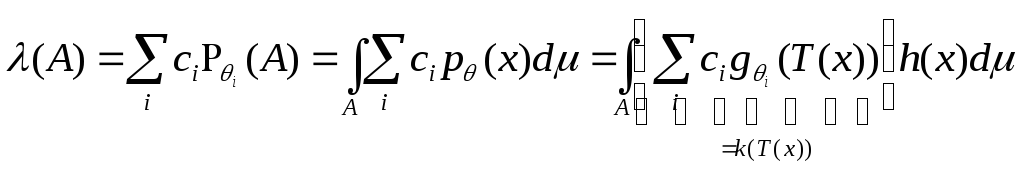
Пусть , тогда

г)Покажем, что

, т.е

- не зависит от Т- дост. статистика

Рассмотрим

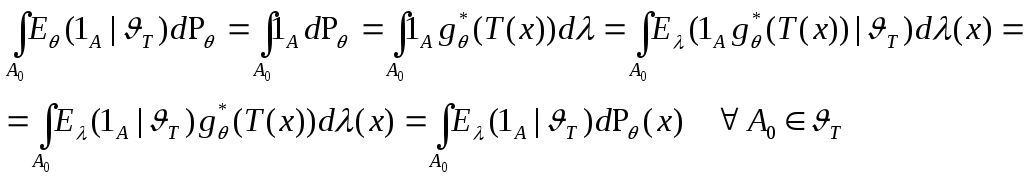
В силу единственности условного мат.ожид

(доказали).

21.Примеры нахождения достаточных статистик.

По теореме факторизации

1.

a)Пусть Х_1,…,Х_n – выборка из нормального распределения N(a,)

данная мера - мера Лебега в Rⁿ

Плотность совместного распределения

b) известно

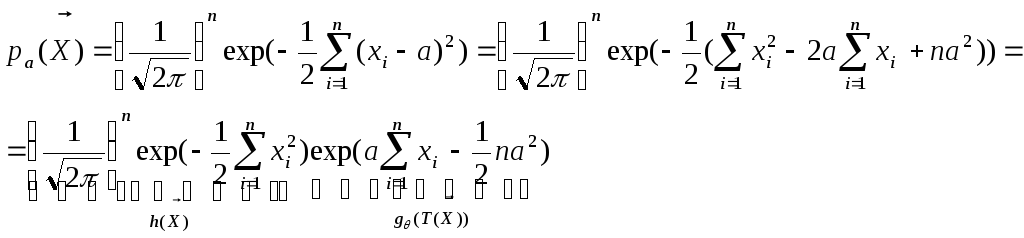
2.Распределение Пуассона
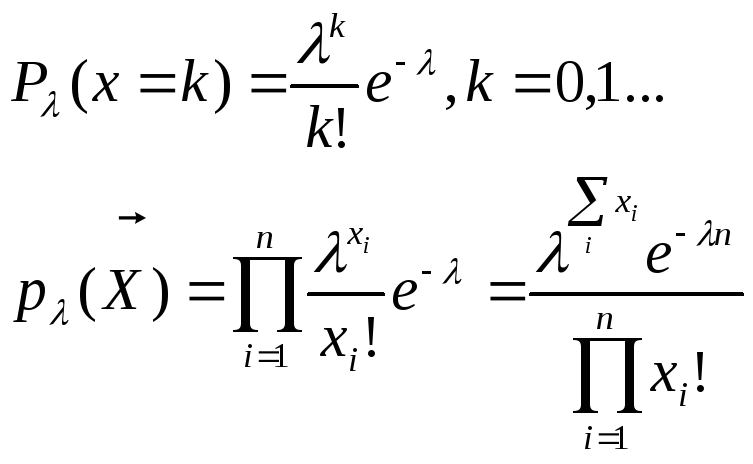
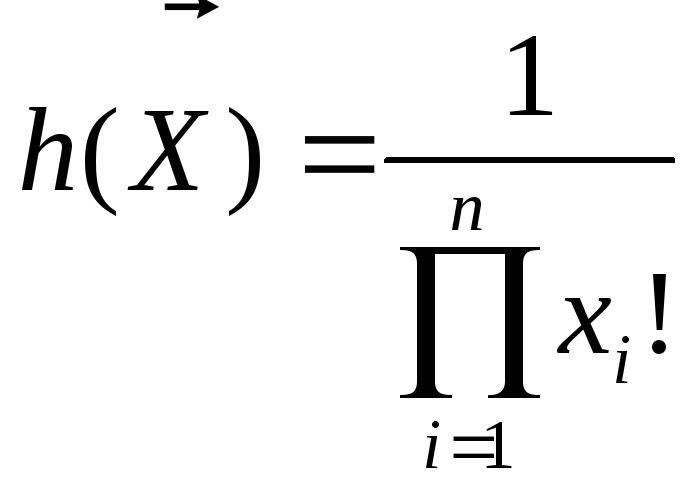