Санкт-Петербургский электротехнический университет имени В. И. Ульянова (Ленина)

Кафедра МО ЭВМ

Минимизация функции алгебры логики

Способы представления функции алгебры логики

Процедура Квайна – Мак-Класки

Метод карт Карно

Минимизация на гиперкубах

Вариант №32

Преподаватель: Факультет	Красюк В. И. КТИ
Студент группы 4305:	Морозов П.

Санкт-Петербург

2008 Г.

Способы представления функции алгебры логики

1. Основные сведения

X– множество логических переменных, определенных на двухэлементном множествеB={0,1} – основное множество алгебры логики. ЕслиY(X) →B, тоY– множество логических функций. Алгебра логики может быть определена как алгебра, содержащая 3 операции “И” (конъюнкция), “ИЛИ” (дизъюнкция), “НЕ”(отрицание) над множеством элементов изX. Результаты выполнения операций над множеством элементов также принимают значения изB.

Xⁿ– пространство кортежей

ЄXⁿ– кортеж

- модуль

- индекс, равен числу единичных значений

Основные способы представления функций алгебры логики:

1. Множества истинности, ложности и неопределенности

2. Аналитический

3. Табличный

4. Графический

2. Представление функции алгебры логики

2.1. Множества истинности, ложности и неопределенности

Множество истинности - множество наборов значений аргументов, на которых функция истинна.

Множество ложности - множество наборов значений аргументов, на которых функция ложна.

Множество неопределенности - множество наборов значений аргументов, на которых функция не определена.

Задание функции :

2.2. Аналитическое представление

Функция представляется с помощью формулы, содержащей переменныеи операции алгебры логики. Однозначно определяют функцию только совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ).

Конституэнта 1– это совершенная конъюнкция, которая принимает значение 1 на одном и только одном наборе значений параметров.

СДНФесть дизъюнкция конституэнт единицы, на которых функция принимает значение 1.

Минимальная форма– такая формула функции алгебры логики, которая содержит не больше символов, чем любая другая формула для данной функции.

СДНФ:

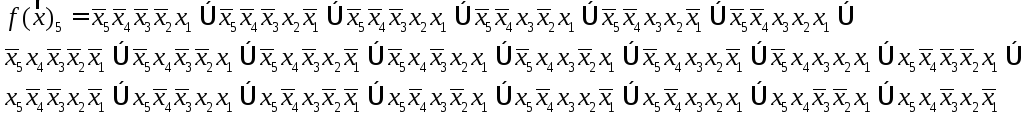
Основная проблема алгебры логики – минимизация формулы функции алгебры логики.

2.3. Табличное представление

В табличном представлении используются:

1. Таблица истинности

2. Прямоугольная таблица

3. Карта Карно

2.3.1. Таблица истинности

В таблице истинности функции - 2ⁿстрок и (n+1) столбец. Строки, содержащие различные комбинации значений аргументов, упорядочены по возрастанию модуля вектора аргументов или, что то же самое, в лексикографическом порядке.

Таблица истинности

	х5	х4	х3	х2	х1
0	0	0	0	0	0	0
1	0	0	0	0	1	1
2	0	0	0	1	0	1
3	0	0	0	1	1	1
4	0	0	1	0	0	0
5	0	0	1	0	1	1
6	0	0	1	1	0	1
7	0	0	1	1	1	1
8	0	1	0	0	0	1
9	0	1	0	0	1	1
10	0	1	0	1	0	1
11	0	1	0	1	1	1
12	0	1	1	0	0	0
13	0	1	1	0	1	1
14	0	1	1	1	0	1
15	0	1	1	1	1	1
16	1	0	0	0	0	0
17	1	0	0	0	1	1
18	1	0	0	1	0	1
19	1	0	0	1	1	1
20	1	0	1	0	0	1
21	1	0	1	0	1	1
22	1	0	1	1	0	1
23	1	0	1	1	1	1
24	1	1	0	0	0	0
25	1	1	0	0	1	1
26	1	1	0	1	0	1
27	1	1	0	1	1	0
28	1	1	1	0	0	0
29	1	1	1	0	1	0
30	1	1	1	1	0	0
31	1	1	1	1	1	0

2.3.2. Прямоугольная таблица

Прямоугольная таблица – другая форма таблицы истинности. Например, для функции в таблице остинности будетn⁵= 32 строки, достаточно много. Можно разделить картеж на 2:. Получится таблица из 8 строк и 4 столбцов:

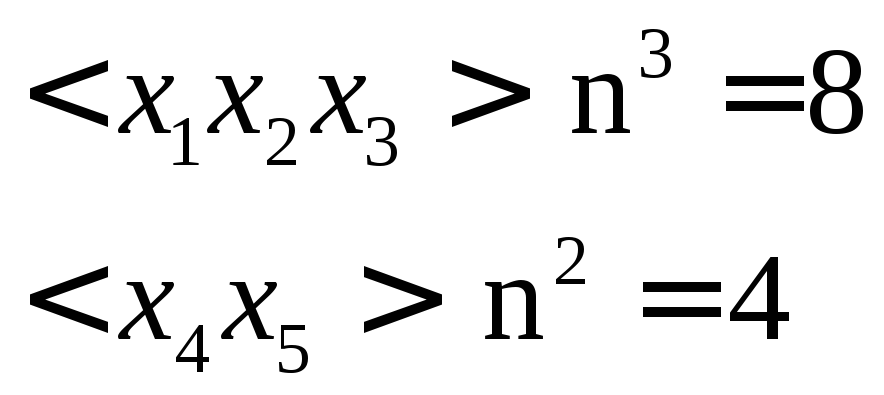
8x4 = 32 элемента, как и в исходной таблице истинности.

	00	01	10	11
000	0	1	0	0
001	1	1	1	1
010	1	1	1	1
011	1	1	1	0
100	0	0	1	0
101	1	1	1	0
110	1	1	1	0
111	1	1	1	0

2.3.3. Карта Карно

Карта Карно является координатным способом представления булевых функций. При этом способе задания таблица истинности функции представляется в виде координатной карты состояний, которая содержит 2ⁿ клеток (по числу входных наборов булевой функции n переменных). Размерность таблицы - при четномN, и при нечетномN. При переходе от четного N к нечетному количество столбцов удваивается. При переходе от нечетного к четному N – удваивается количество строк.

Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца карты, а другая - координаты строки. При такoм способе построения каждая клетка определяется значениями переменных, соответствующих определенному двоичному набору. Внутри каждой клетки карты Карно ставится значение функции на данном наборе. Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е были соседними. Такой способ представления очень удобен для наглядности при минимизации булевых функций.

Карта Карно

х₅

х₄

х₃

х₂

х₁

x5x4x3 x2x1	000	001	011	010	110	111	101	100
00	0 0 00000	0 4 00100	0 12 01100	1 8 01000	0 24 11000	0 28 11100	1 20 10100	0 16 10000
01	1 1 00001	1 5 00101	1 13 01101	1 9 01001	1 25 11001	0 29 11101	1 21 10101	1 17 10001
11	1 3 00011	1 7 00111	1 15 01111	1 11 01011	0 27 11011	0 31 11111	1 23 10111	1 19 10011
10	1 2 00010	1 6 00110	1 14 01110	1 10 01010	1 26 11010	0 30 11110	1 22 10110	1 18 10010

2.4. Графическое представление

При графическом представлении используетсяn-мерный куб. С вершинами гиперкуба связаны следующие числовые характеристики:

1. Весом (илинормой)вершины с координатами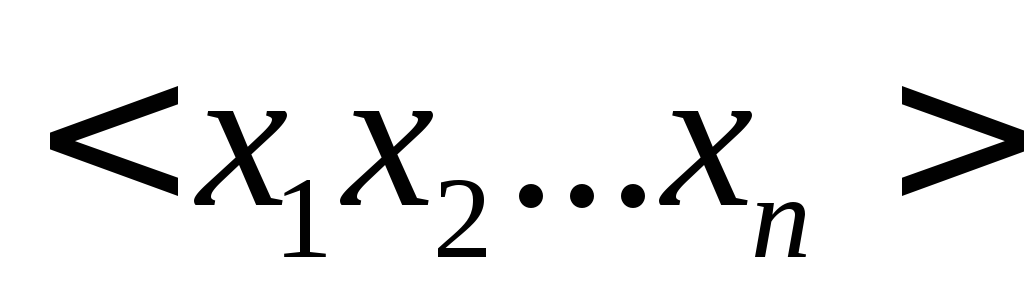называется сумма всех ее координат, т.е..

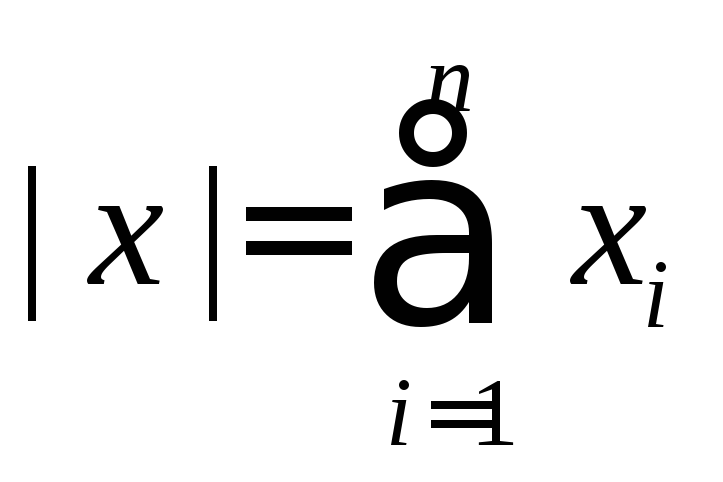2. Номером вершины 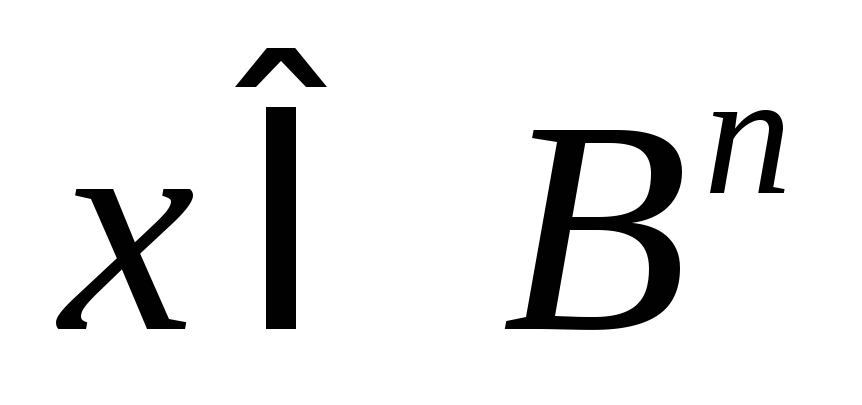называют модуль 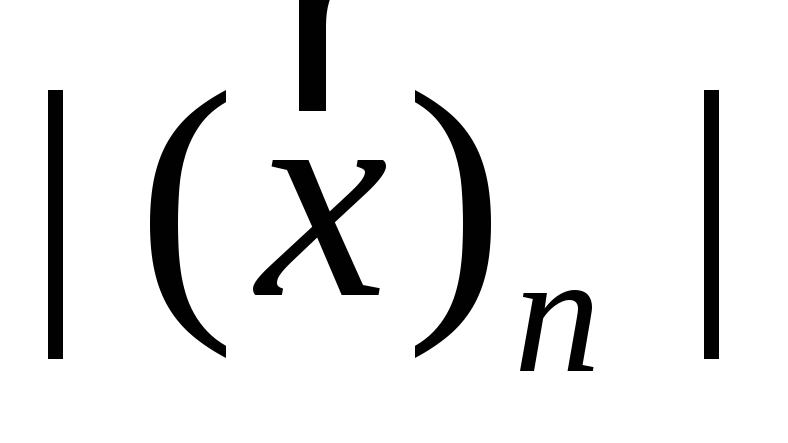. Следовательно, номера вершин гиперкуба 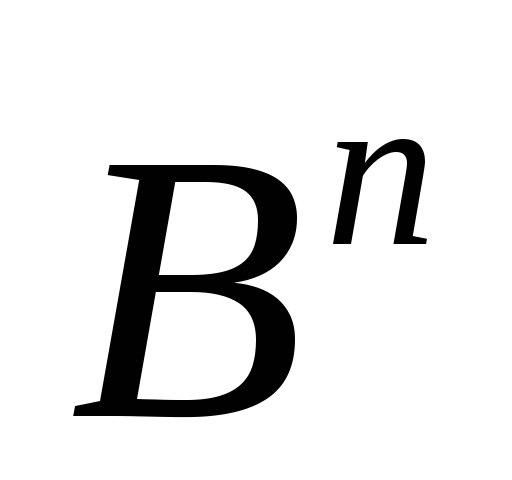- это целые числа из интервала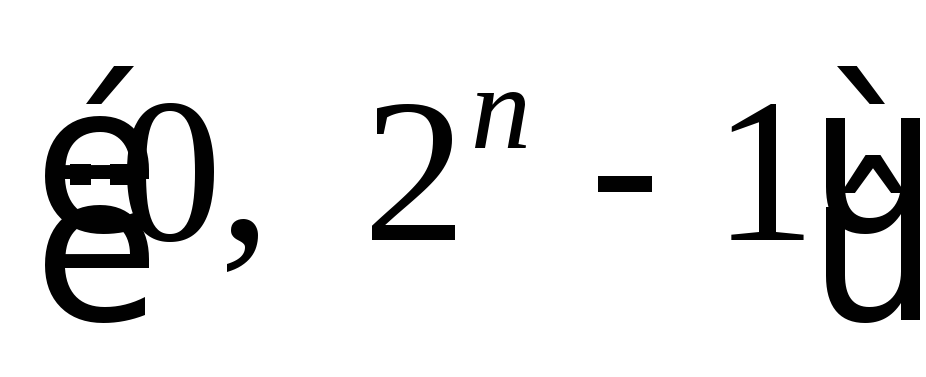, а соответствующие им вершины есть двоичное представление этих чисел.

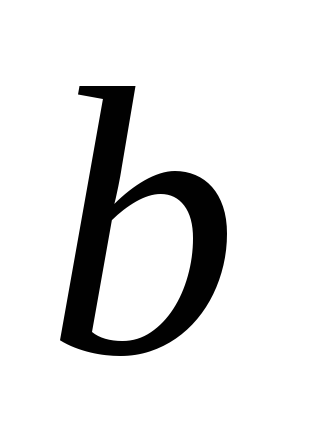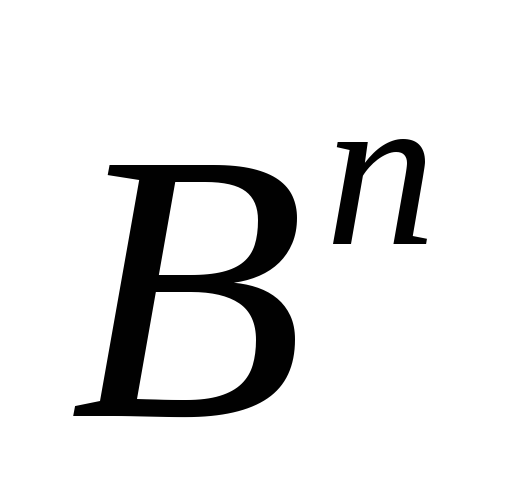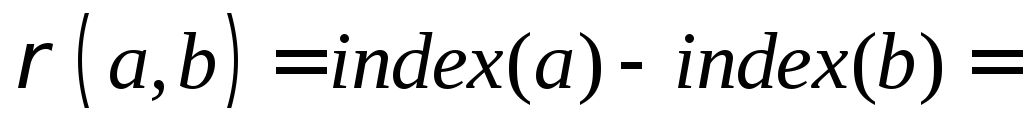
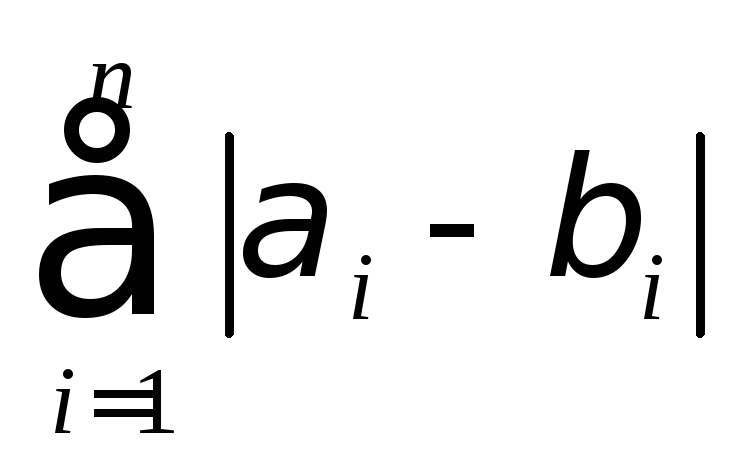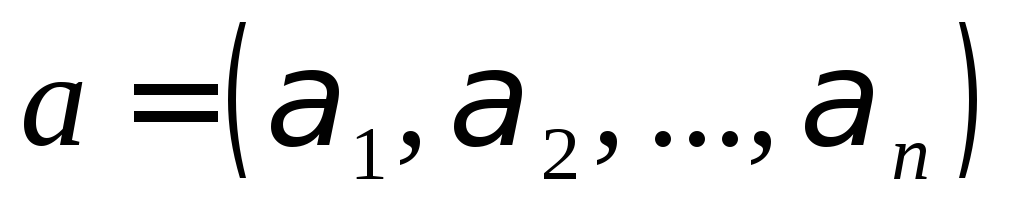3. Расстоянием Хэммингамежду вершинамиигиперкуба называется разность индексов, гдеи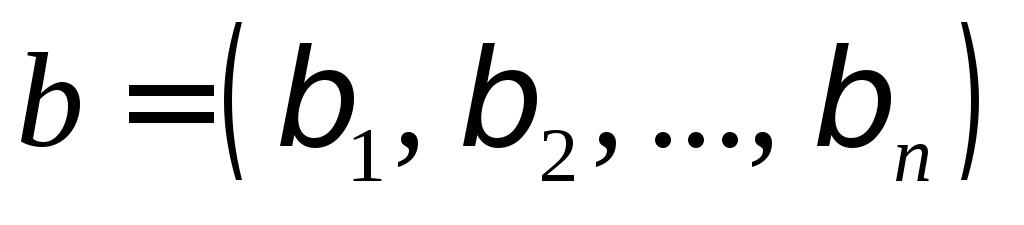, т.е. расстояние между двумя вершинами – это число координат, которыми они различаются.

Используя данные числовые характеристики, можно выделять различные подмножества гиперкуба.

1. Вершины и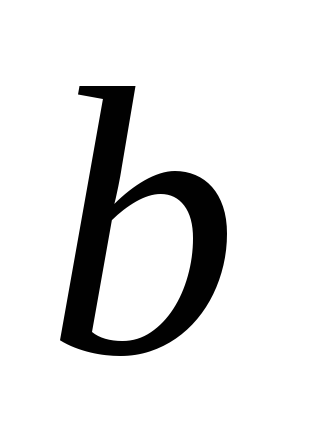гиперкуба 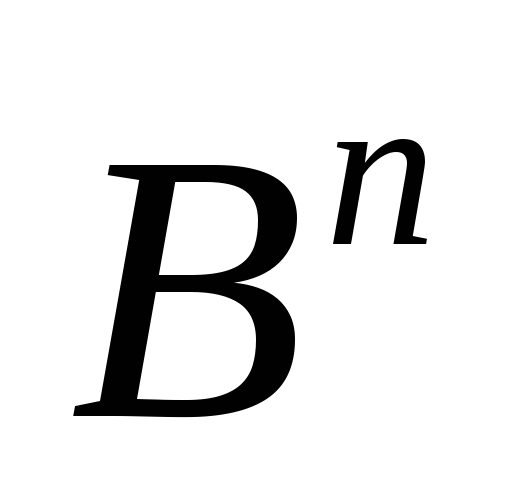называютсясмежными,если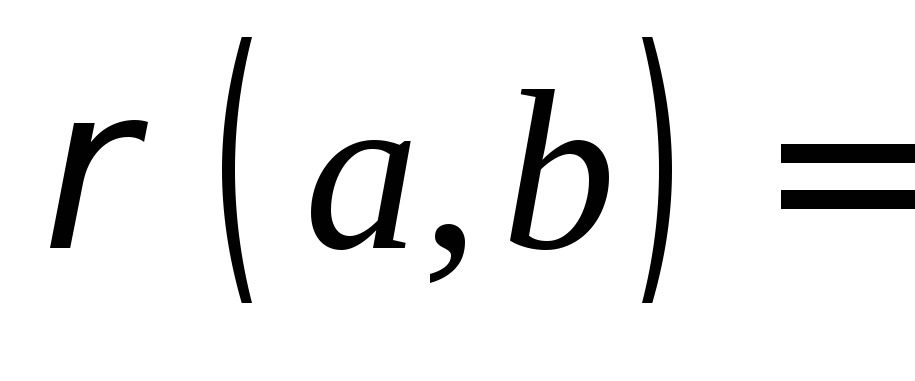1, а неупорядоченная пара смежных вершин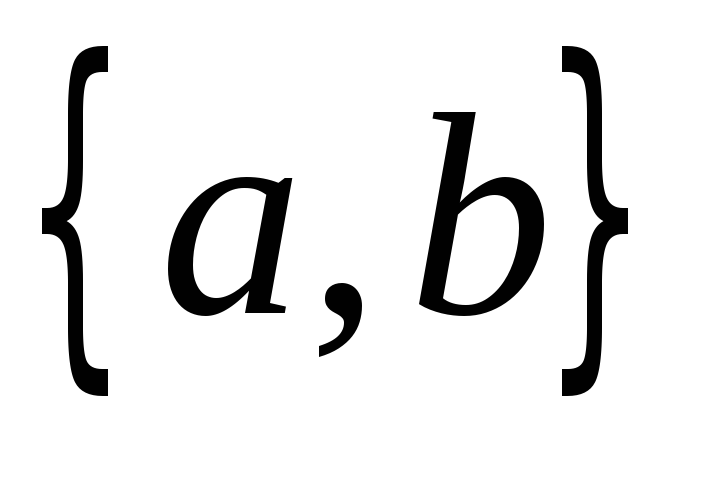называетсяребром гиперкуба .

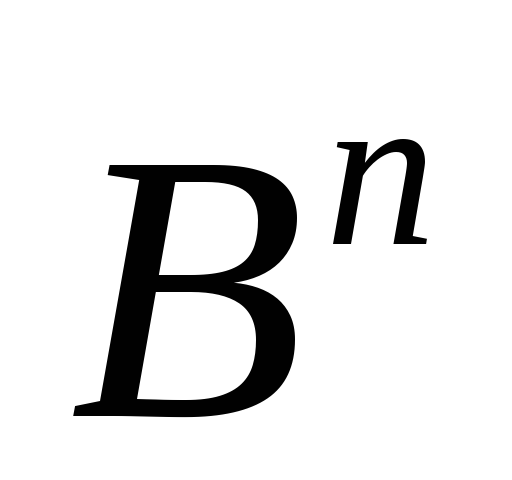2. Вершины и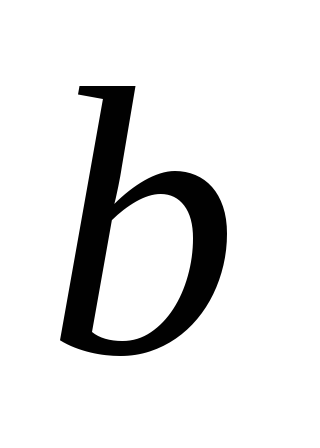гиперкуба 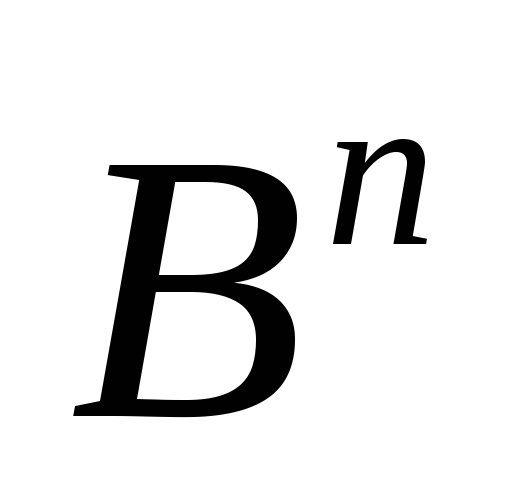называютсяпротивоположными,если.

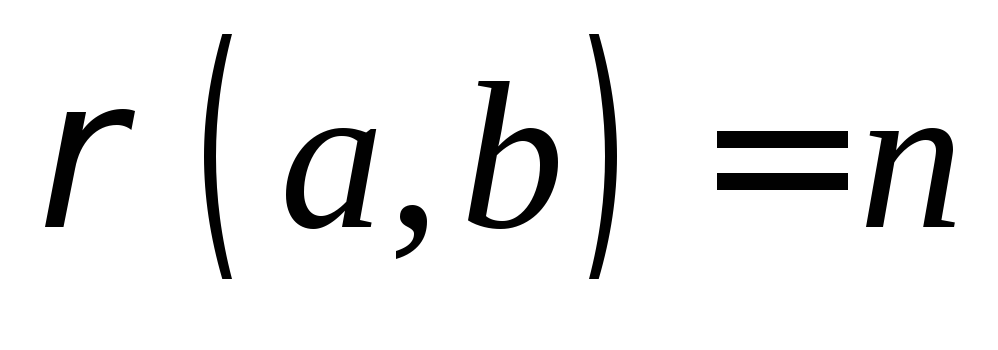3. Два ребра гиперкуба называются смежными,если они имеют общую вершину, а упорядоченная последовательность попарно смежных ребер называетсяцепью гиперкуба. Такую цепь проще задавать упорядоченной последовательностью попарно смежных соседних вершин, например,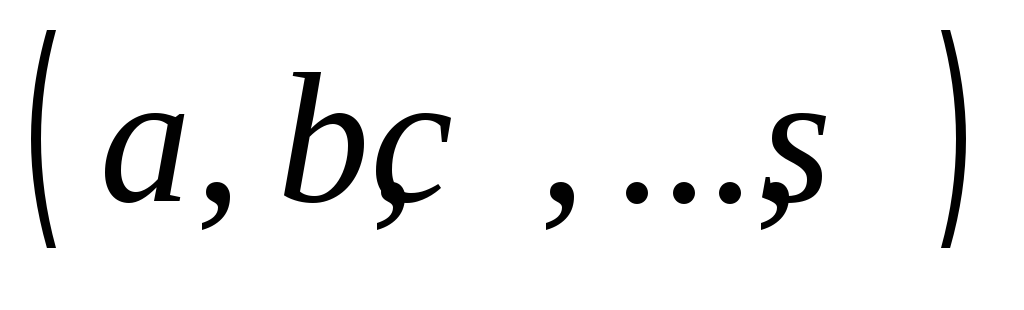- цепь, связывающая вершиныи, где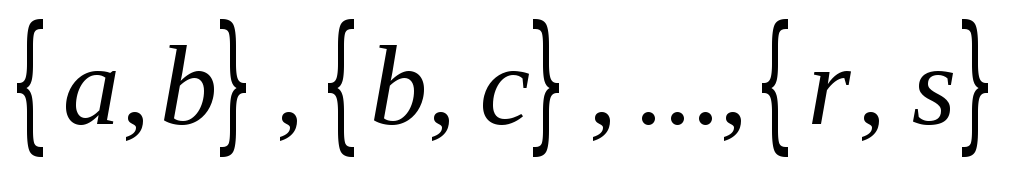- попарно смежные ребра.

Представление с помощью гиперкуба:

Процедура Квайна – Мак-Класки