Лабораторная работа 6 / Попытка сделать ЛР6

Санкт-Петербургский Государственный Электротехнический Университет «ЛЭТИ»

Кафедра АПУ

Отчет

по лабораторной работе №6

по дисциплине «Теория автоматического управления»

«Анализ устойчивости нелинейных систем»

Выполнили:

студенты гр. 4322

факультет КТИ

Миненков Д.В.

Золотарев А.Р.

Проверил:

Имаев Д. Х..

СПб 2007 г.

Цель работы: применение первого и второго метода Ляпунова для анализа осциллятора с нелинейным демпфированием.

Математическая модель осциллятора имеет вид:

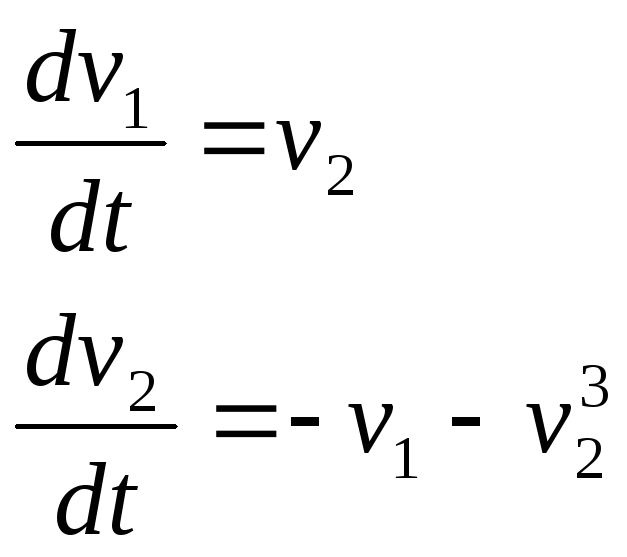(естественный базис)

Найдем положения равновесия, т.е. положения, в которых производные от переменных состояния равны нулю:

«Перенесем» начало координат в точку равновесия системы:

Необходимо исследовать устойчивость этого положения равновесия.

1. Применение первого метода Ляпунова.

Применение первого метода сводится к исследованию линеаризованных уравнений.

Пусть переменных малы. Тогда в исходных уравнениях состояния можно пренебречь членом , в результате чего получим линейные уравнения:

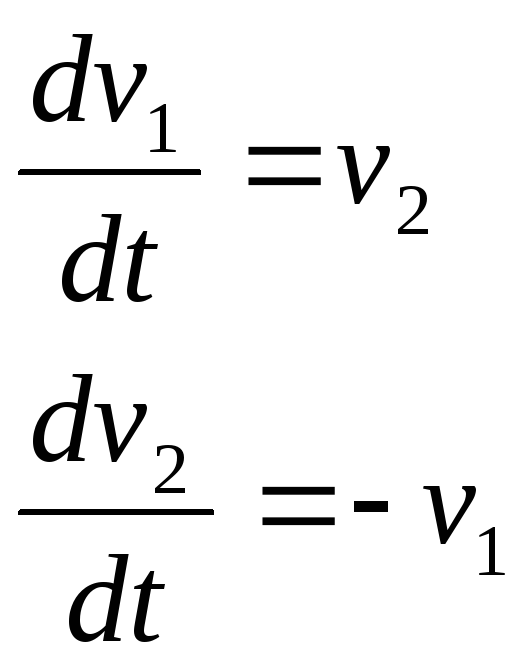
Запишем систему уравнений состояния в матричной форме:

Или:

Характеристический полином матрицы А:

Корни характеристического полинома:

,

Т.е. корни находятся на границе устойчивости. Таким образом, первый метод Ляпунова не позволяет сказать что-то об устойчивости положения равновесия, т.к. неизвестно, как действует член, которым мы пренебрегли на расположение полюсов.

2. Второй (прямой) метод Ляпунова

Второй метод Ляпунова не связан с линеаризацией.

Выберем положительно – определенную функцию:

Найдем производную этой функции по времени:

В силу диф. уравнений системы, имеем:

Функция обращается в ноль в точке равновесия (0).

Получили отрицательную знакопостоянную функцию, следовательно, положение равновесия устойчиво.

3. Компьютерное моделирование.

А) Смоделируем систему, полученную по первому методу Ляпунова:

Структура системы на рисунке 1.

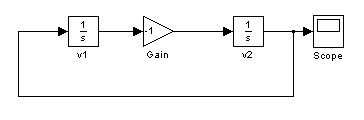
Рис.1. Линеаризованная система.

Как и следовало ожидать, в такой системе наблюдается колебательный процесс:

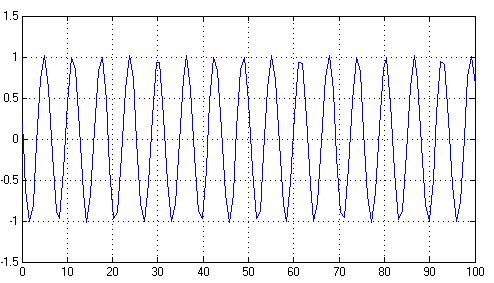
Рис.2. Процессы в системе

Б) Моделирование нелинеаризованной системы:

Рис.3. Нелинеаризованная система.

В такой системе реакция на начальные условия 0.05 и -0.05 :

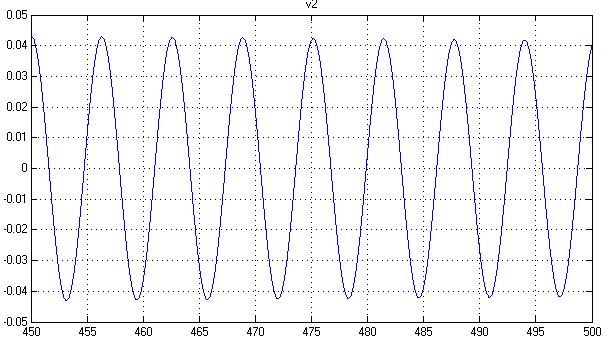
Рис.4. Реакция на НУ.

По рисунке 2 о положении равновесия ничего сказать нельзя. Однако если рассмотреть 2 соседних пика:

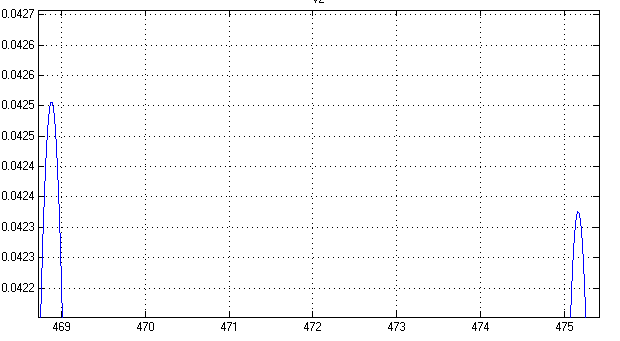
то видно затухание колебаний, т.е. процессы затухают при .

Вывод: компьютерное моделирование не дает нам ответ на вопрос об устойчивости системы. Только второй метод Ляпунова позволяет сделать вывод об устойчивости.

Фазовый портрет системы:

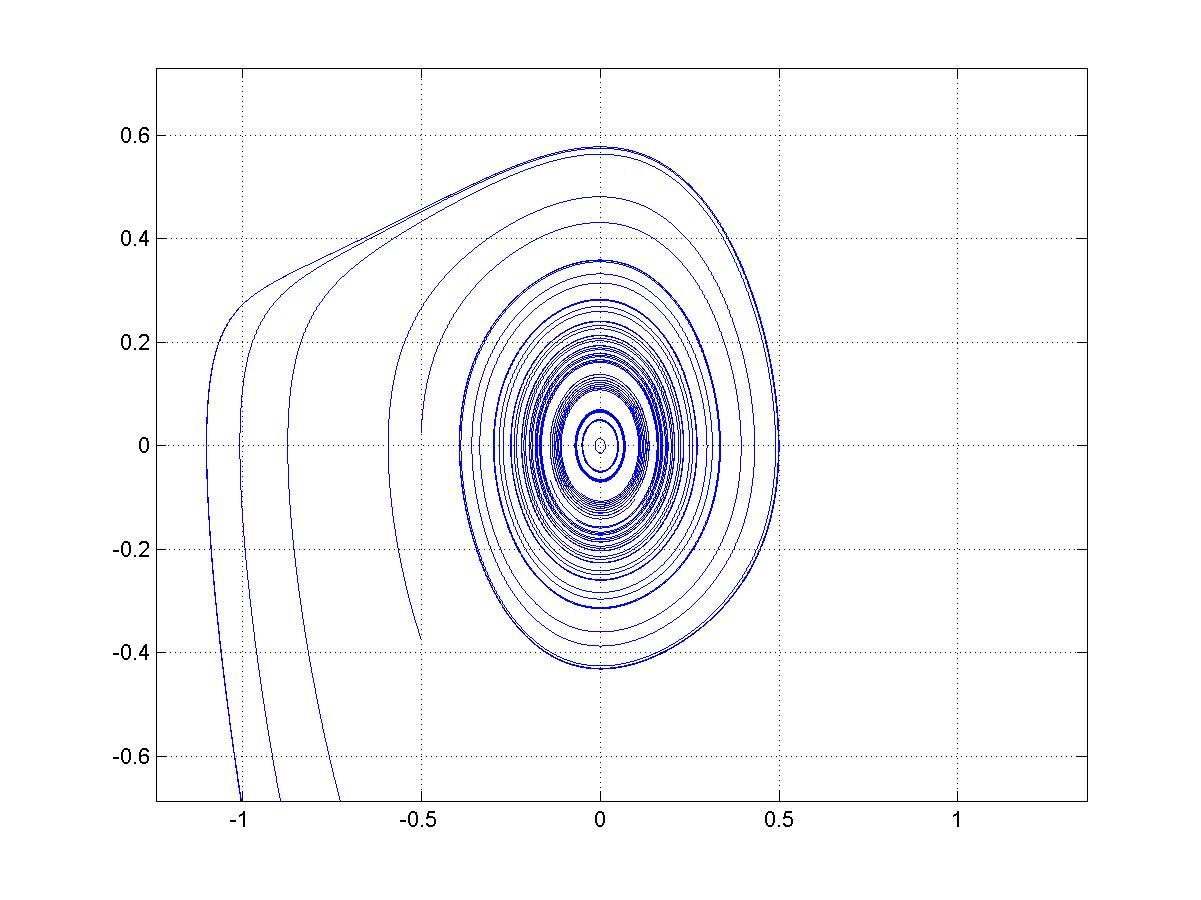
Рис.6. Фазовый портрет.

4. Аналитический способ

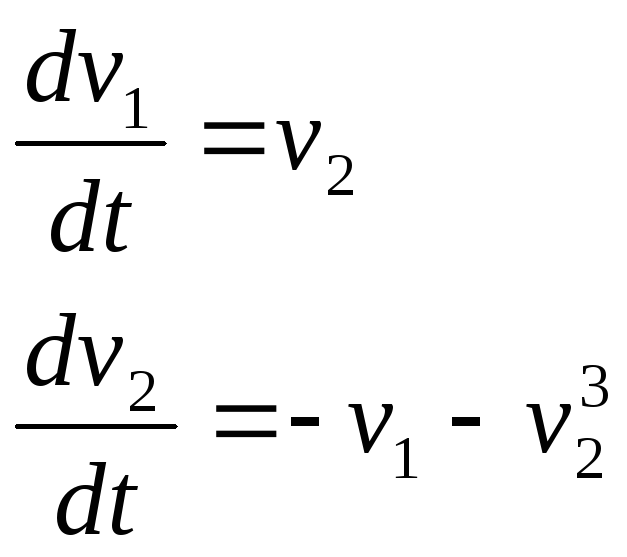
Разделим одно уравнение на другое:

Не удается разделить переменные.

Проведем компьютерное моделирование, задав структурную схему:

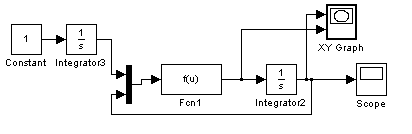
Рис.7. Структурная схема

В блоке функции задано: -(u[1]+ u[2]^3)/ u[2]).

5. Анализ устойчивости нелинейной системы, заданной в форме структурной схемы.

На рисунке 8 изображена структурная схема:

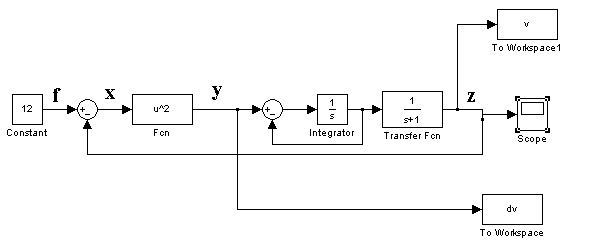
Рис.8. Структурная схема.

5.1. Найдем точки равновесия

=0

Т.е. действительные решения получи при

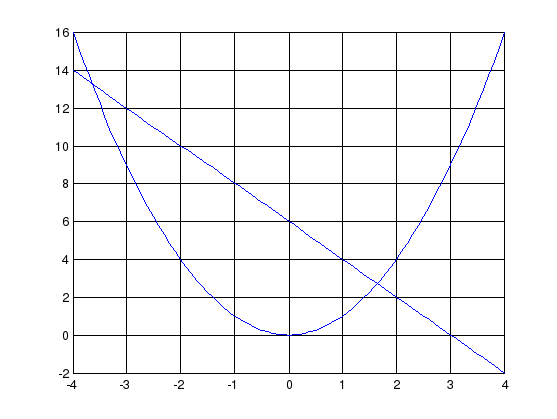
Рис.9.

Пусть f=12. Тогда:

; ;

5.2 Исследование первым методом Ляпунова.

Линеаризация:

5.3. Анализ устойчивости линеаризованной системы

Характеристический полином замкнутой системы.

- все коэффициенты больше нуля, условие устойчивости выполнено

- условие устойчивости не выполнено

5.4. Фазовый портрет нелинейной системы

1) устойчивый фокус

2) неустойчивый узел

Построим фазовый портрет, построив систему в Simulink:

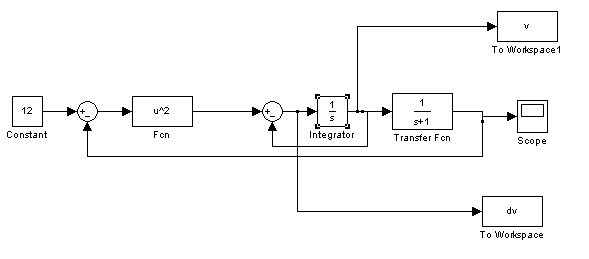
Рис.10. Структурная схема системы.

В результате получим фазовый портрет системы:

Рис. 11. Фазовый портрет.

На рисунке 11 четко видны устойчивый фокус в точке (9,0j) и неустойчивый узел в точке (16, 0j).