Лекция №2

Непараметрические методы классификации

Алгоритмы распознавания образов часто классифицируют как параметрические и непараметрические. Для некоторых задач бывает априорно известно, что образы характеризуются рядом параметров. Параметрический подход может основываться на дискриминантных функциях, связанных с классом плотностей вероятностей, определяемых относительно малым числом параметров. С другой стороны, существуют другие классификаторы, в которых не делается никаких предположений о характеризующих параметрах. Несмотря на то, что параметризация дискриминантных функций (т.е. коэффициенты многомерных полиномов) используется в непараметрических методах, не предполагается соответствующей формы распределения. В этом состоит отличие от параметрического представления.

В параметрических методах обычно предполагается, что классы образов порождаются многомерными нормальными распределениями. Далее рассмотрим основы построения непараметрических классификаторов.

2.1. Решающие поверхности и дискриминантные функции

Как было показано в лекции 1, каждый образ отображается в виде точки в пространстве образов. Образы, относящиеся к разным классам, попадают в разные области в пространстве классов и, соответственно, могут быть разделены разделяющими поверхностями.

Разделяющие поверхности, называемые решающими поверхностями, могут быть формально определены как поверхности вn-мерном пространстве, которые используются, чтобы разделить известные образы на их соответствующие категории и используются для классификации неизвестных образов.

Такие поверхности можно определить как гиперплоскости, имеющие размерность n-1. Когдаn<1 решающая поверхность представляет собой точку, как показано на рис.2.1., где точка А разделяет классыw₁иw₂ и точка В — разделяющая точка дляw₂иw₃.

Рис. 2.1.

Когда n=2 решающая поверхность становится линией

w_1*x₁+w_2*x₂+w₂=0

как показано на рис.2.2.

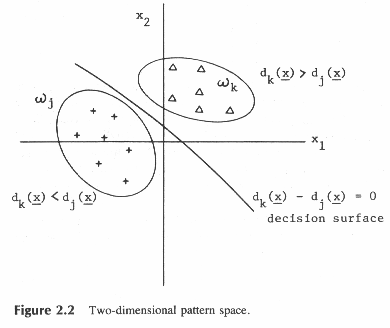
Рис. 2.2.

Когда n=3 — поверхность является плоскостью, дляn=4 или больше — это гиперплоскость

w_1*x₁+w_2*x₂+……….w_к*x_к+w_к=0,

представимая в матричной форме как

W^т_*Х=0, где , ,

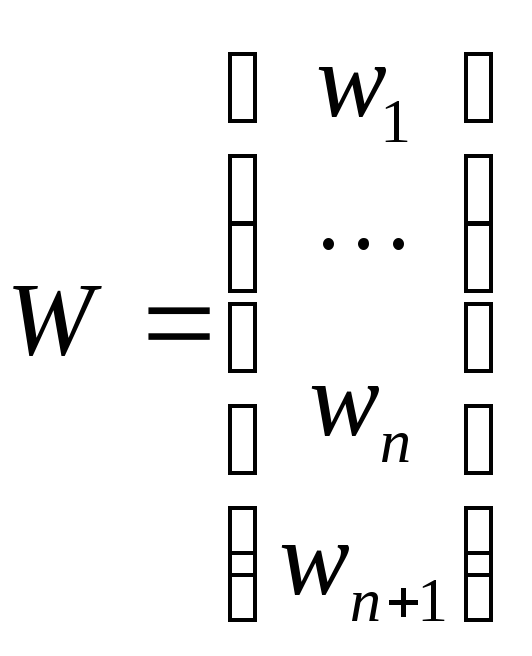где Wи Х называютсярасширенным весовым векторомирасширенным вектором образа.

Для удобства скаляр w_n+1добавлен в весовой вектор и, соответственно, векторстановится (n+1)-мерным путем добавленияx_n+1=1.

Это позволяет представить все линейные дискриминантные функции проходящими через начало координат.

Дискриминантная функция — это функция d(), которая определяет решающую поверхность. Как показано на рис.2.2. d_k(Х) и d_j(Х) — являются дискриминантными функциями для образа Х в классах k и j соответственно.

d(Х)= d_k(Х) - d_j(Х)=0 будет уравнением, которое определяет поверхность, разделяющую классы k и j.

Мы можем сказать, что d_k(Х) > d_j(Х)xw_k ,jk,j=1, 2, 3, …M.

Система для классификации образа Х показана на рис.2.3.

Рис.2.3. Схематическая диаграмма построения простой классификационной системы .

d₁(Х) = d₂(Х)

или

d(Х)= d₁(Х) – d₂(Х)=0

будет определять разделяющую гиперплоскость между двумя классами.

В общем случае для М различных классов требуется М(М-1)/2 разделяющих поверхностей, но некоторые из них избыточны. Вообще, для разделения М классов достаточно М-1 поверхностей.

На рис.2.4. показан для двумерного пространства ряд разделяющих поверхностей как функции числа категорий, на которые надо классифицировать.

На рис.2.4а представлена решающая поверхность, разделяющая 2 категории.

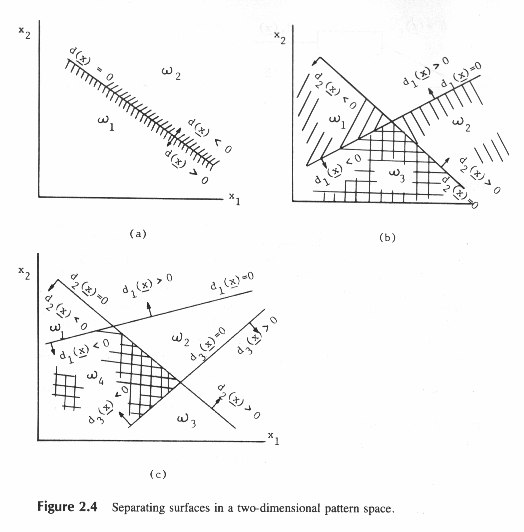
Рис.2.4. достаточно понятен.

Здесь есть область d₁(Х) < 0; d₂(Х) < 0.

Она не принадлежит w₁и w₂ и может быть названа w_{3 .}

То же самое имеет место на рис.2.4с.

Здесь области:

W₁ : d₁(Х) > 0;

W₂ : d₂(Х) > 0; d₁(Х) < 0

W₃ : d₂(Х) < 0; d₃(Х) > 0

Область:

d₁(Х) < 0

d₃(Х) < 0 не определена

d₂(Х) < 0

Пример:для М=2 классов найдем дискриминантную функцию для классификации двух образов на две категории

И

Возьмем d(Х) = Х₁– ½Х₂ – 2 и проверим

d(Х₁) =w^’_{* 1} = (1 – ½ – 2)= -3 < 0

d(Х₂) =w^’_{* 2} = (1 – ½ – 2)= +1 > 0

Т.е. d(Х) можно использовать как дискриминантную функцию.