Дискриминантный анализ.
Дискриминантный анализ представляет статистический аппарат для изучения различий между двумя и более группами объектов по отношению к нескольким переменным одновременно.
"Дискриминантный анализ" - это общий термин, относящийся к нескольким тесно связанным статистическим процедурам. Их можно разделить на методы интерпретации межгрупповых различий и методы классификации наблюдений по группам. При интерпретации необходимо ответить на вопросы: возможно ли, используя данный набор характеристик (переменных), отличить один класс от другого. Метод, относящийся к классификации, связан с получением одной или нескольких функций, обеспечивающих возможность отнести данный объект к одной из групп. Рассмотрим это наиболее подробно.
Задача классификации состоит в отнесении некоторого элемента выборки w к одной из k групп W1, W2, ... , Wk на основе измерения р параметров х1,..., хр.
Классификация в случае многомерных нормальных выборок с известными параметрами.
Стандартная процедура классификации для случая р непрерывных переменных предполагает, что наблюдения принадлежат одной из двух групп, имеющих многомерные нормальные распределения. Наблюдения х1, х2 ,..., xp записываются в виде вектора
X = ( x1, ... , xp ) T
и предполагается, что W1 имеет распределение:
,
W2 - распределение:
Другое предположение состоит в том, что
i=1,..p ; j=1..p
Итак, вектор X имеет распределение:
или
Параметры m1 , m2 , e вначале будут считаться заданными. Найдем линейную комбинацию наблюдений, называемую дискриминантной функцией, имеющую вид:
z=a1*x1 + ... + ap*xp , (1)
где a1 , ... , ap - некоторые постоянные, и отнести X к W1, если z>=c и к W2 , если z<c ,
где с - постоянная.
Тогда задача будет сведена к определению значений a1 , ... , ap и с, минимизирующих вероятность ошибочной классификации.
Если наблюдение X поступило из W1 , то величина z имеет нормальное распределение со средним
и дисперсией
Аналогично для X из W2 величина z имеет нормальное распределение со средним
и с той же дисперсией. Имеет смысл выбрать такие a1 , ... , ap , при которых V1 , V2 были бы как можно больше удалены друг от друга относительно sz2 . Для этого введем расстояние Махаланобиса
Эта величина была предложена в работе Mahalanobis(1936) для измерения “расстояния” между двумя группами. Таким образом требуется найти коэффициенты a1 , ... , ap , максимизирующие D2 . В работе Fisher(1936) показано, что такие ai служат решением системы линейных уравнений
a1*s11 + a2*s12 + ... + ap*s1p = m1 1 - m21
a1*s21 + a2*s22 + ... + ap*s2p= m1 2 - m22
...
a1*sp1 + a2*sp2 + ... + ap*spp= m1 p - m2p
После подстановки полученных ai в (1) каждому объекту ставится в соответствие значение дискриминантной функции z.
Для определения постоянной с следует рассмотреть вероятности ошибок Pr(1|2) и Pr(2|1). Естественно искать такую постоянную с , чтобы сумма вероятностей Pr(1|2)+Pr(2|1) была минимальной. Это можно достигнуть выбором постоянной с , равноудаленой от средних,
т. е.
Приведем теперь более строгое решение задачи классификации, основанное на теореме Байеса. Определим вначале априорную вероятность qi как вероятность того, что элемент выборки принадлежит к группе Wi, i=1,2. Сумма априорных вероятностей q1+q2 равна 1.
Определим далее условную вероятность Pr(x|Wi) получения некоторого вектора наблюдений X , если известно, что объект принадлежит группе Wi. Обозначим также через Pr(Wi|X) условную вероятность того, что объект принадлежит группе Wi при данном векторе наблюдений X. Эта величина называется апостериорной вероятностью.
Теорема Байеса. Равенство
справедливо для любого распределения величин X.
Если X имеет многомерное нормальное распределение
или
,
то Pr(X|W1) и Pr(X|W2) можно заменить соответственно
на плотности распределений f1(X) и f2(X). В
результате получим
i=1,2.
(2)
Байесовская процедура классификации состоит в отнесении вектора наблюдений X к W1,если Pr(W1|X) >= Pr(W2|X) , и к W2 , если Pr(W1|X) < Pr(W2|X).
Подставляя в эти неравенства значения апостериорных вероятностей из (2) получаем, что X относится к группе W1 , если
и к W2 , если
Такая процедура минимизирует ожидаемую вероятность ошибочной классификации
q1Pr(2|1)+q2Pr(1|2).
Заметим , что эта величина является вероятностью того , что объект , принадлежащий группе W1 , ошибочно классифицируется , как принадлежащий W2 , или наоборот объект из W2 ошибочно относится к W1.
Алгебраическими преобразованиями неравенства (3) можно показать , что байесовская процедура эквивалентна отнесению X к W1 , если
и к W2 , если
Постоянные ai являются решениями системы уравнений (1) , а V1 , V2 заданы выше.
Введем в байесовскую процедуру понятие стоимости ошибочной классификации . Для этого введем величину C(2|1) - стоимость потери из-за отнесения объекта из W1 к W2 . Аналогично, C(1|2) - стоимость потери из-за отнесения W2 к W1.
Обобщенная процедура классификации Байеса состоит в отнесении X к W1 , если
и к W2 , если
Такая процедура минимизирует ожидаемую стоимость ошибочной классификации
q1C(2|1)Pr(2|1)+q2 C(1|2)Pr(1|2).
Для обобщенной байесовской процедуры вероятности ошибочной классификации имеют вид
и
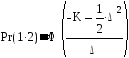
где
Решение системы (1) можно записать в матричных обозначениях
a = e-1( m1-m2 ) ,
где a = ( a1 , ... , ap )T.
Расстояние Махалонобиса
D2 = ( m1-m2 ) T e-1( m1-m2 ) .