Лабораторная работа 3 / 2008-05-07-23-25-Маша-LR-3

Санкт-Петербургский

государственный электротехнический

университет «ЛЭТИ»

кафедра АПУ

Отчет

по лабораторной работе по ОТУ №3

Параметрическая оптимизация систем управления

Группа: 5362

Проверил: проф. Имаев Д.Х.

Санкт-Петербург

2008 год

Целью данной лабораторной работы является параметрическая оптимизация системы управления.

Математическая модель в форме структурной схемы (рис. 1).

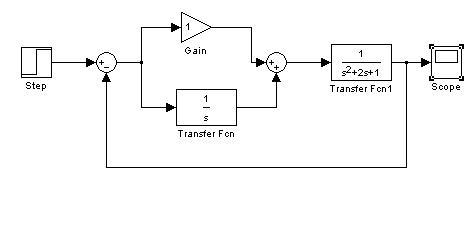
Рис. 1.

Параметры регулятора: k;Т.

ХПЗС = числитель + знаменатель ПФРС,

где ХПЗС – характеристический полином замкнутой системы;

ПФРС – передаточная функция разомкнутой системы.

ПФРС: .

ХПЗС: , где

коэффициенты:

a₃=;

a₂=;

a₁=;

a₀=1.

Проверим необходимое условие устойчивости (все коэффициенты должны быть положительны); оно выполняется.

Воспользуемся критерием Гурвица, для этого составим матрицу Гурвица:

H=

Критерий Гурвица заключается в том, чтобы проверять знаки диагональных миноров.

;

, но так как a₀ >0 всегда, то надо проверять только знак .

Следует заметить, что средние коэффициенты играют стабилизирующую роль, а крайние – дестабилизирующую.

В условие устойчивости параметры входят в символьном виде; запишем их в явном виде:

(должно быть) или 2T(1+k)-1>0.

Это выражение позволяет выделить на плоскости k, T область устойчивости (рис.2).

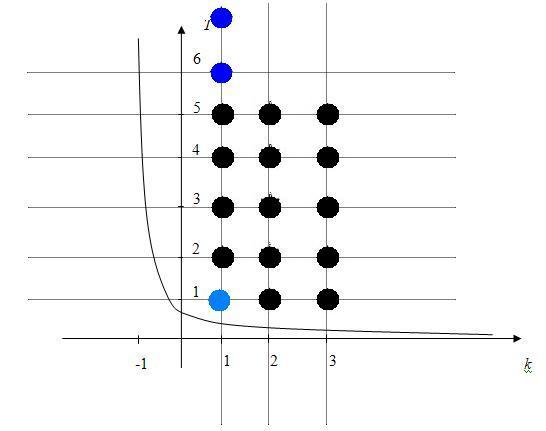
Рис. 2

Отметим три типа различных корней соответствующими символами:

Границу устойчивости получим, заменив неравенство на знак равенства

;

это гипербола, если k= -1, то гипербола уходит в бесконечность.

Возможны 3 случая:

1. 3 корня отрицательные вещественные;

2. пара комплексных и 1 действительный корень, при этом доминируют комплексные корни:

3. пара комплексных и 1 действительный корень, при этом доминирует действительный корень.

Можем воспользоваться двумя способами:

1. MATLAB/Control System Toolbox

2. Simulink.

Воспользуемся первым из них. Назначим

>>k=1;T=1;

Передаточную функцию разомкнутой системы получим по команде:

>>osys = (k+tf(1,[T 0]))*tf(1,[1 2 1])

Transfer function:

s + 1

---------------

s^3 + 2 s^2 + s

замыкаем единичную отрицательную обратную связь:

>>csys = feedback(osys,1)

Transfer function:

s + 1

---------------------

s^3 + 2 s^2 + 2 s + 1

Проверим устойчивость системы, проверяя корни ХПЗС (собственные значения матрицы системы):

>>eig(csys)

ans =

-1.0000

-0.5000 + 0.8660i

-0.5000 - 0.8660i

Найдем границы областей с различным характером движения, для этого выбираем точки и соответственно получаем области с 3 типами распределения корней.

1. При k=0 и T>6.8 корни вещественные <0;

2. При k=1 и T=1, при k=0.5 и T=0.5 получаем второй случай, когда доминируют 2 комплексных корня;

3. При k=2 и T=1, k=2 и T=2, k=1 и T=3 точки попадают в область, где доминирует действительный корень.

Проанализируем ПХ с помощью команды:

>> step(csys)

Результаты представлены на рис. 3.

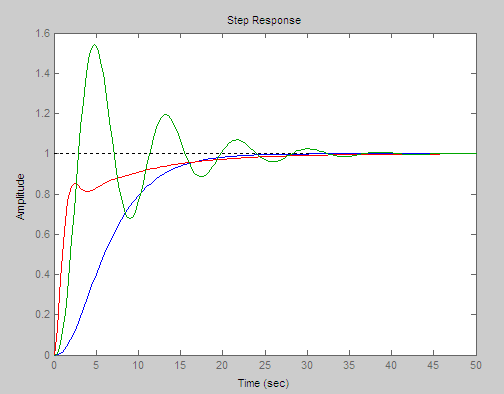
Рис. 3.

Выберем критерий оптимальности в виде минимума времени процесса:

t_p → min

при ограничении

Находим k и T оптимальное:

k = 1.19;

T = 1.15;

t_p = 4.44 c

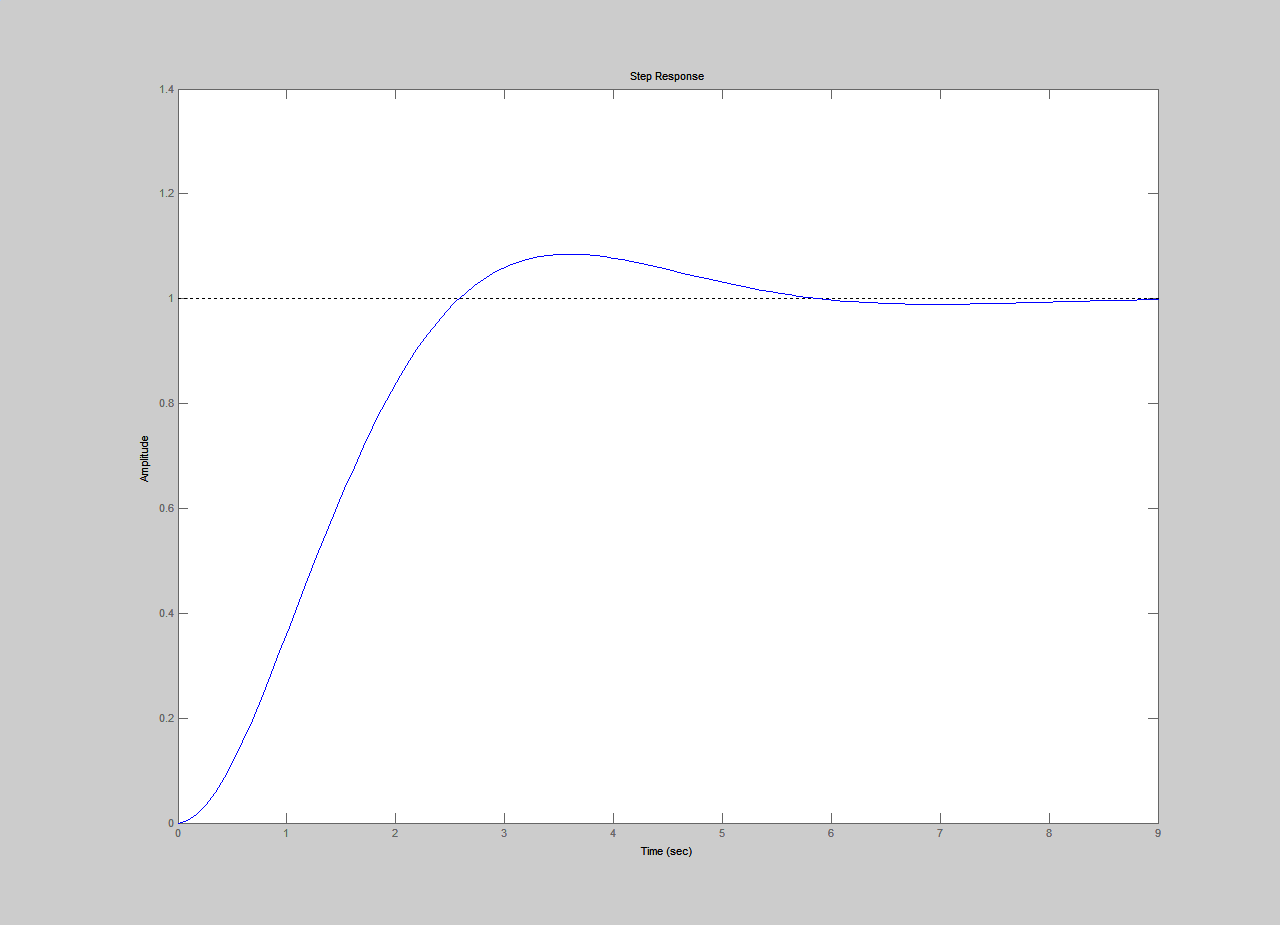
Рис. 4

Для этого сделаем еще несколько шагов влево, вправо, вверх и вниз.

Пусть k=1.584 и T=1.15, тогда , следовательно, точка (1.32; 1.15) не оптимальна.

Пусть k=1.9 и T=0.89, тогда , следовательно, точка (1.9; 0.89) не оптимальна

Пусть k=1.9 и T=1.45, тогда , следовательно, точка (1.9; 1.45) не оптимальна

Пусть k=1.9 и T=1.15, тогда , следовательно, точка (1.584; 1.15) не оптимальна

Пусть k=2.2810 и T=1.15, тогда , следовательно, точка (1.9008; 1.15) оптимальна.

Получим ПХ (рис. 5) с помощью команды:

>> step(csys)

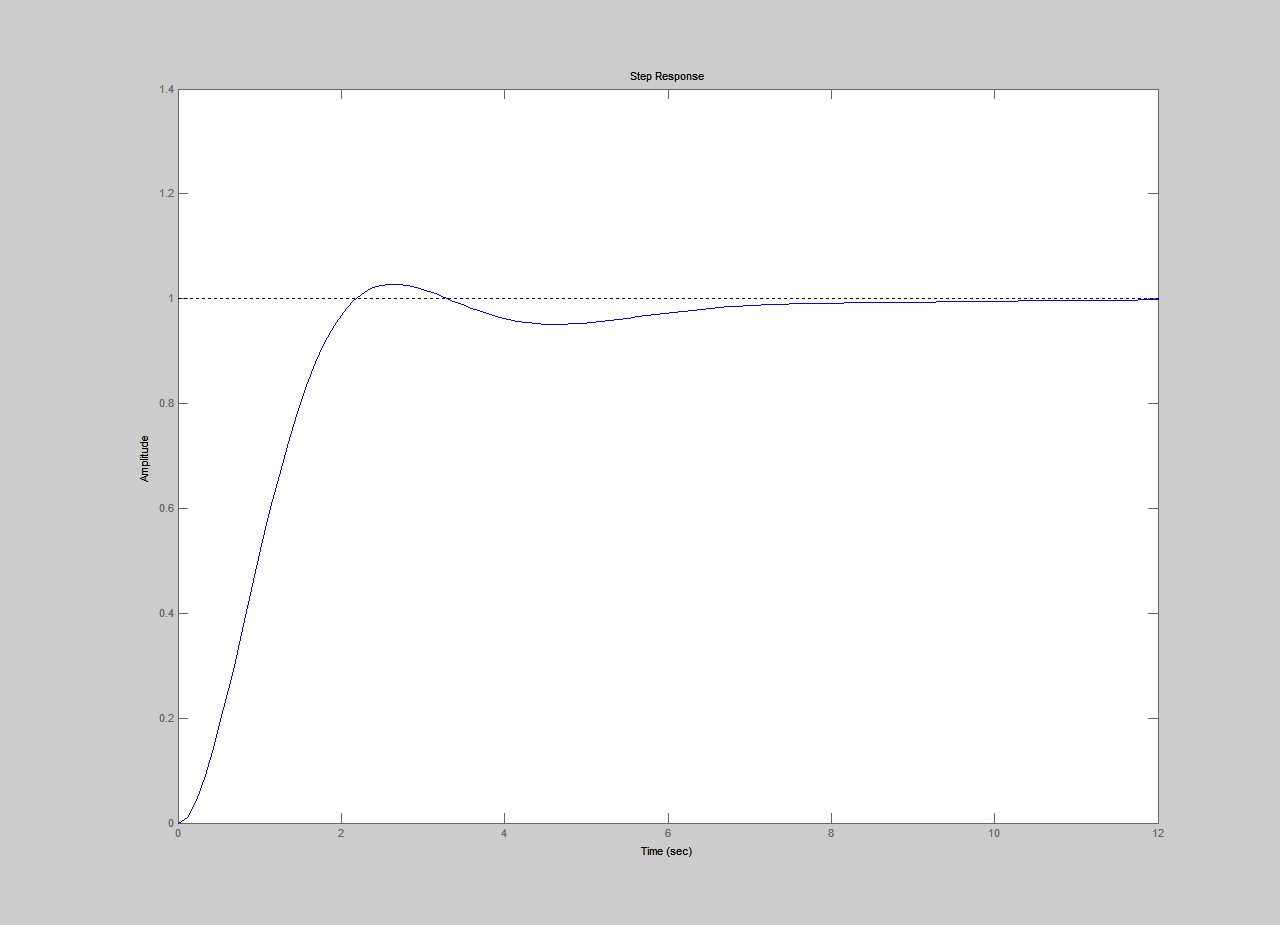
Рис. 5

Получим ЛЧХ и ФЧХ для разомкнутой системы (рис. 6).

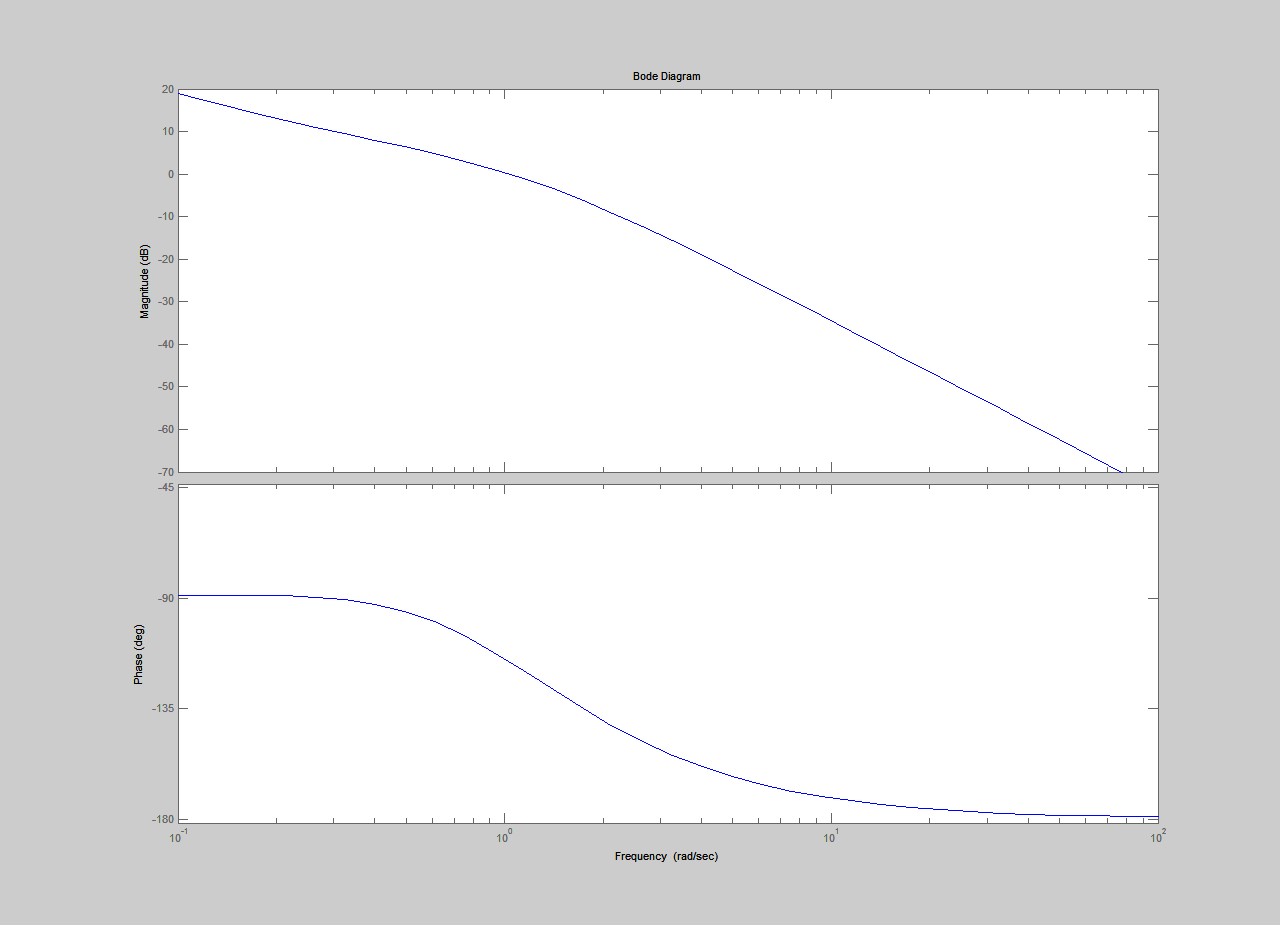
Рис. 6

Выводы:

1. в данной работе найдена область устойчивости системы.

2. нашли оптимальное значение k=1.9 и T=1.15, так как значение является минимальным при этом корни ХПЗС получились равными:

-0.841 + .428i

-0.841 - 1.428i

-0.316 _.