10 Решение системы, в котором все свободные переменные полагаются равными нулю, называется базисным

(количество возможных базисных решений равно количеству вариантов определения базисных переменных).

Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений. Алгоритм симплекс-метода всегда начинается с некоторого допустимого базисного решения и затем пытается найти другое допустимое базисное решение, "улучшающее" значение целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в небазисные. Это необходимо, чтобы новое решение содержало в точности m базисных переменных. В соответствии с терминологией симплекс-метода выбранная нулевая переменная называется вводимой (в базис), а удаляемая базисная переменная — исключаемой (из базиса).

11 Условие допустимости. Как в задаче максимизации, так и в задаче минимизации в качестве исключаемой выбирается базисная переменная, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно.

Последовательность действий, выполняемых в симплекс-методе.

Шаг 1. Находится начальное допустимое базисное решение.

Шаг 2. На основе условия оптимальности определяется вводимая переменная. Если вводимых переменных нет, вычисления заканчиваются.

Шаг 3. На основе условия допустимости выбирается исключаемая переменная.

Шаг 4. Методом Гаусса-Жордана вычисляется новое базисное решение. Переход к шагу 2.

Задача условной оптимизации формулируется следующим образом:

f (x) = f (x₁, x₂, ..., x_n) Юextr,

j _i (x) = j _i(x₁, x₂, ..., x_n) = 0, , m < n.

12 Метод Гаусса-Жордана отличается от метода Гаусса тем, что при выполнении вычислений прямого хода на k-м шаге делим k-е уравнение на a^(k-1)_kk (не равное  0) и выполняем дальнейшие вычисления с ведущим элементом, равным единице.

Тогда в конце прямого хода имеем

а в конце обратного хода —

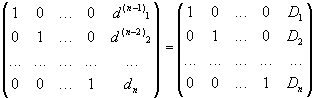
и тогда очевидно последний столбец содержит решение системы.

13 когда исходное ограничение записано в виде равенства или имеет знак “³”, нельзя сразу же получить допустимое начальное базисное решение.

Покажем это на следующем примере:

z = 4x1 + x2 ® min, (13)

3x1 + x2 = 3,

4x1 + 3x2 ³ 6, (14)

x1 + 2x2 £ 4,

x1, x2 ³ 0.

Чтобы записать задачу в стандартной форме, введем в левую часть второго ограничения избыточную переменную x3 , а в левую часть третьего – остаточную переменную x4. В результате система ограничений примет вид:

3x1 + x2 = 3,

4x1 + 3x2 - x3 = 6, (15)

x1 + 2x2 + x4 = 4,

x1 , x2, x3, x4 ³ 0.

Таким образом, имеются три уравнения, содержащие четыре неизвестных. Это означает, что каждому базисному решению соответствует одна не базисная переменная (равная нулю). В отличие от случая, когда каждое уравнение содержит остаточную переменную, в данной ситуации уже нельзя быть уверенным в том, что при нулевом значении одной из переменных все базисные переменные будут неотрицательными.

Идея использования искусственных переменных предполагает включение неотрицательных переменных в левую часть каждого из уравнений, не содержащих «очевидных» начальных базисных переменных. Эти переменные

играют роль остаточных и используются только для получения начального базиса, причем в процессе оптимизации они принимают нулевые значения, обеспечивая допустимость оптимума.

Разработаны два тесно связанных между собой метода получения начального базиса, в каждом из которых используется «штрафование» за использование искусственных переменных. Рассмотрим каждый из них на при-

мере сформулированной выше задачи.

M-метод (метод больших штрафов)

Рассмотрим линейную модель (13), (14), приведенную к cтандартной форме (13), (15). В первом и втором уравнениях нет переменных, выполняющих роль остаточных. Поэтому введем в каждое из этих уравнений по одной искусственной переменной, обозначив их через p1 и p2 :

3x1 + x2 + p1 = 3,

4x1 + 3x2 - x3 + p2 = 6.

За использование этих переменных в состав целевой функции введем штраф, приписывая им достаточно большой положительный коэффициент М. (В задаче максимизации искусственным переменным следует приписать в

целевой функции достаточно большой по абсолютной величине отрицательный коэффициент -М (М>0)) В итоге будет получена следующая линейная модель:

z = 4x1 + x2 + Mp1 + Mp2 ® min,

3x1 + x2 + p1 = 3,

4x1 + 3x2 - x3 + p2 = 6,

x1 + 2x2 + x4 = 4,

x1 , x2, x3, p1, p2, x4 ³ 0.

Имеются три уравнения и шесть неизвестных. Следовательно, начальное базисное решение должно включать 6 - 3 = 3 нулевые переменные. Если положить равными нулю переменные x1 , x2 и x3, то сразу же будет получено

требуемое начальное допустимое решение: p1 = 3 , p2 = 6 , x4 = 4 .

Для решения задачи симплекс-методом необходимо исключить базисные переменные из целевой функции, для чего подставим в целевую функцию выражения для искусственных переменных, полученные из соответствующих ограничений

p1 = 3- 3x1 – x2 ,

p2 = 6 – 4x1 – 3x2 + x3.

В результате получается следующее выражение для z:

z = 4х1 + х2+ М(3- Зх1 – х2) + М(6 - 4х1 – Зх2 + x3)=

=(4 - 7М)x1 + (1- 4М)x2 + Mx3 + 9M.

При этом z-уравнение в симплекс-таблице будет иметь вид

z - (4 - 7М)x1 - (1- 4М)x2 - Mx3 = 9M.

Таким образом, начальному решению, в котором x1 = x2 = x3 =0, соответствует значение z = 9М, как это и должно быть при p1=3 и p2= 6.

Ниже представлена последовательность симплекс-таблиц, приводящих к оптимальному решению задачи.

х1 х2 x3 p1 p2 х4

p1 3 3 1 0 1 0 0

p2 6 4 3 -1 0 1 0

х4 4 1 2 0 0 0 1

z 9M -4 + 7M -1 + 4M -M 0 0 0

х1 1 1 1/3 0 1/3 0 0

p2 2 0 5/3 -1 -4/3 1 0

х4 3 0 5/3 0 -1/3 0 1

z 4+2M 0 (1+5M)/3 -M (4-7M)/3 0 0

х1 3/5 1 0 1/5 3/5 -1/5 0

х2 6/5 0 1 -3/5 -4/5 3/5 0

х4 1 0 0 1 1 -1 1

z 18/5 0 0 1/5 8/5 – M -1/5 – M 0

х1 2/5 1 0 0 2/5 0 -1/5

х2 9/5 0 1 0 -1/5 0 3/5

x3 1 0 0 1 1 -1 1

z 17/5 0 0 0 7/5 – M -M -1/5

Поскольку в строке z все коэффициенты неположительные (M – большое положительное число), то оптимальному решению соответствует точка x*=2/5, x*= 9 / 5, в которой zmin = 17/5. Так как в оптимальном решении отсутствуют искусственные переменные, имеющие положительные значения, данное решение является допустимым оптимальным решением задачи в ее исходной постановке, т. е. до введения искусственных переменных. В случае, когда задача не имеет допустимого решения, в полученном оптимальном решении, по крайней мере, одна искусственная переменная будет отлична от нуля.

14 четыре особых случая, встречающихся при использовании симплекс-метода.

1). Вырожденность.

2). Альтернативные оптимальные решения.

3). Неограниченные решения.

4). Отсутствие допустимых решений.

Вырожденность

В ходе выполнения симплекс-метода проверка условия допустимости может привести к неоднозначному выбору исключаемой переменной. В этом случае на следующей итерации одна или несколько базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным.

В вырожденном решении нет никакой опасности, за исключением небольших теоретических неудобств, которые мы далее кратко обсудим. С практической точки зрения вырожденность объясняется тем, что в исходной задаче присутствует, по крайней мере, одно избыточное ограничение. Для того чтобы лучше понять практические и теоретические аспекты явления вырожденности.

Альтернативные оптимальные решения

Когда прямая (если рассматривается двухмерная задача ЛП, в общем случае - гиперплоскость), представляющая целевую функцию, параллельна прямой (гиперплоскости), соответствующей связывающему неравенству (которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение на некотором множестве точек границы пространства решений. Эти решения называются альтернативными оптимальными решениями.