
- •Введение
- •Задание
- •1. Построение моделей
- •1.2. Линейная модель
- •1.2. Степенная модель
- •1.3. Показательная модель
- •1.4. Гиперболическая модель
- •2. Проверка адекватности однофакторного регрессионного уравнения
- •2.1. Анализ показателей качества подгонки регрессионного уравнения.
- •2.4. Проверка выполнения условий для получения «хороших оценок» методом наименьших квадратов
- •3. Сводная таблица по лабораторной работе
- •4. Расчет прогнозного значения
- •Заключение
- •Список использованной литературы:
2.4. Проверка выполнения условий для получения «хороших оценок» методом наименьших квадратов
МНК даёт «хорошие» оценки коэффициентов и при выполнении нескольких условий; эти условия касаются Ei, основными предположениями классической модели линейной регрессии является:
1. М( i)=0; Во всех моделях. Отсюда следует, что первое условие выполняется для всех моделей.
2.
Среди основных условий регрессий
присутствует следующее условие
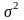 =const.
Одним из критериев выполнения этого
условия является то, что величина F
подчиняется F-распределению
со степенями свободы n1=n/2-1
и n2=n/2-1.
=const.
Одним из критериев выполнения этого
условия является то, что величина F
подчиняется F-распределению
со степенями свободы n1=n/2-1
и n2=n/2-1.
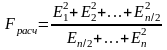
Fрасч определено для каждой модели, и представлено в сводной таблице. В итоге, с вероятностью 95% можно сказать, что условие 2 выполняется для всех моделей, т.к. Fрасч меньше Fтабл.
Модели адекватны, модели не нужно улучшать.
3. Следующим условием определения «хороших оценок» коэффициентов регрессии является отсутствие зависимости между случайными компонентами. Выполнение этого условия можно проверить с помощью критерия Дарвина-Уотсена, вычисляемого по следующей формуле:
D=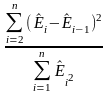
Рассчитаем данные показатели для всех моделей:
Для линейной модели он будет равен:
D = 6476,371/3957,859=1,64
Для степенной модели:
D = 0,0024/0,0013=1,86
Для показательной модели:
D = 0,0025/0,0012=2,04
Для гиперболической модели:
D = 6772,135/5026,95=1,35
Решения принимаются на основе табличных данных из следующих правил:
1. d2<D-W<2;
2. D-W<d1;
3. d1<D-W< d2;
4. 2<D-W
Если d расч меньше 2, и больше d2 = 1,36, то это значит, что гипотеза об отсутствии автокорреляции принимается. Для линейной, степенной и показательной модели гипотезу об отсутствии принимаем с вероятностью 0,95.
Таким образом, условие 3 выполняется для линейной, степенной и показательной модели (все расчетные и фактические данные приведены в сводной таблице). Итак, можно сделать вывод, что условия «хороших оценок» выполняются для линейной, степенной и показательной модели.
Рассчитаем
также среднюю относительную ошибку Е .
.
Е
=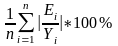
Для линейной модели он будет равен:
Е =0,35
Для степенной модели:
Е =0,32
Для показательной модели:
Е =0,36
Для гиперболической модели:
Е =0,3
Если Е меньше 15%, то модель построена на высоком уровне точности.
Следовательно, все модели построены с приемлемой точностью.
3. Сводная таблица по лабораторной работе
№ задания |
Oбозначение |
Формула |
Значение |
Примечание |
|||||||||||||||||||
Линейная модель |
Степенная модель |
Показательная модель |
Гиперболическая модель |
||||||||||||||||||||
y=a+bx |
Y=AX^B |
Y=AB^X |
Y=A+B/X |
||||||||||||||||||||
|
y=lgY,a=lgA,x=lgX,b=B |
y=lgY,x=X,a=lgA,b=lgB |
y=Y ,x=1/X, a=A, b=B |
||||||||||||||||||||
1 |
В своем виде |
Y=-2,952+1,0656x |
Y= 0,9557*X1,017 |
Y= 169,057* 1,00229 x |
Y=944,04-206632/x |
||||||||||||||||||
Линейном виде |
y=-2,952+1,0656x |
y=-0,02+ 1,017x |
y= 2,228+ 0,00099x |
y=944,04-206632x |
|||||||||||||||||||
a |
â
=
= |
-2,952 |
-0,023 |
2,404 |
1416,099 |
|
|||||||||||||||||
b |
1,0656 |
1,017 |
0,001 |
-464946,861 |
|||||||||||||||||||
A |
|
a |
10^a |
10^a |
a |
||||||||||||||||||
-2,952 |
0,949 |
253,591 |
1416,099 |
||||||||||||||||||||
B |
|
b |
b |
10^b |
b |
||||||||||||||||||
1,0656 |
1,017 |
1,002 |
-464946,861 |
||||||||||||||||||||
2.1 |
2.1.1 |
Остаточная дисперсия |
= |
878,414 |
0,0004 |
0,00039 |
848,109 |
Чем меньше остаточная дисперсия, тем лучше регрессионное уравнение, (является размерной величиной) |
|||||||||||||||
2.1.2 |
Индекс корреляции |
r = |
0,959 |
Связь прямая сильная |
0,956 |
Связь прямая сильная |
0,951 |
Связь прямая сильная |
0,96 |
Связь прямая сильная |
ryx>0 – прямая связь ryx<0 – обратная связь
|
||||||||||||
2.1.3 |
Коэффициент детерминации |
R =1- |
0,92 |
Хорошее качество подгонки |
0,91 |
Хорошее качество подгонки |
0,9 |
Хорошее качество подгонки |
0,92 |
Хорошее качество подгонки |
0 |
||||||||||||
2.1.4 |
Коэффициент эластичности |
Эyx= |
1,0041 |
1,008 |
0,156 |
-0,9889 |
Показывает на сколько изменился результативный признак y(расч) при изменении факторного признака x на 1 % |
||||||||||||||||
2.1.5 |
Бета-коэффициент |
= |
0,9585 |
0,9555 |
0,9509 |
-0,96 |
Бета-коэффициент
показывает, на какую величину Sy
изменится
в среднем значение y
при изменении величины x
на Sx
, то есть y
изменится на
|
||||||||||||||||
Средние квадратичес-кие ошибки выборки величины y и x |
Sy= |
61,987 |
0,0583 |
0,058 |
92,987 |
||||||||||||||||||
Sx= |
83,637 |
0,0547 |
83,637 |
0,0002 |
|||||||||||||||||||
2.2 |
Значимость уравнения множествен-ной регрессии в целом (F-критерий Фишера) |
F расч= = |
90,434 |
Линейная связь есть |
83,944 |
Линейная связь есть |
75,531 |
Линейная связь есть |
93,952 |
Линейная связь есть |
Если Fтабл > Fрасч, то гипотезу об отсутствии линейной связи отвергаем с заданной вероятностью p. Для Fтабд используются степени свободы n1=1, n2=n-2 |
||||||||||||
Fтабл= 5,32
|
|||||||||||||||||||||||
2.3 |
Значимость коэффициентов уравнения регрессии (t-критерий Стьюдента) |
tрасч
=
|
9,51 |
X влияет на Y существенно |
9,162 |
X влияет на Y существенно |
8,69 |
X влияет на Y существенно |
-9,693 |
X не влияет на Y |
Если t(расч)>t(табл), то x влияет на y существенно, то есть b не равно 0, с заданной вероятностью p. Для t(табл) исп-ся степень свободы n-2 |
||||||||||||
Стандартная ошибка коэффициента b |
|
0,112 |
0,111
|
0,000076 |
47968 |
t(табл)=2,306
|
|||||||||||||||||
2.4 |
2.4.1 |
M( |
|
0,00
|
1 условие M( )=0 соблюдается |
0,00
|
1 условие M( )=0 соблюдается |
0,00
|
1 условие M( )=0 соблюдается |
0,00
|
1 условие M( )=0 соблюдается |
Проверка H0: среднее арифметическое значение уровней ряда остатков по модулю равно 0, на уровне значимости. Но гипотеза отклоняется, если t(табл)> t(расч) со степенью свободы n-1 |
|||||||||||
Среднеквад-ратическое отклонение |
S |
6 |
0,005 |
0,006 |
6 |
||||||||||||||||||
Среднеарифметическое значение уровня ряда |
|
0,00 |
0,00 |
0,00 |
0,00 |
|
|||||||||||||||||
2.4.2 |
D(
)=const= |
|
1,2 |
Дисперсия уменьшается. 2 условие D( )=const выполняется |
2,0 |
Дисперсия уменьшается. 2 условие D( )=const выполняется |
2,5 |
Дисперсия уменьшается. 2 условие D( )=const выполняется |
0,7 |
Дисперсия уменьшается. 2 условие D( )=const выполняется |
Если Fтабл > Fрасч, то гипотезу об уменьшении дисперсии принимаем с заданной вероятностью p.Для Fтабл используем степени свободы n1=n/2-1, n2=n/2-1 |
||||||||||||
Fтабл=6,39
|
|||||||||||||||||||||||
2.4.3 |
Cov( |
d расч = |
1,64 |
По критерию D-W ряд остатков не коррели рован. 3 условие Cov =0 выполняется |
1,86 |
По критерию D-W положительная автокорреляция присутствует . 3 условие Cov( =0 нарушается |
2,04 |
По критерию D-W ряд остатков не коррелирован. 3 условие Cov( =0 выполняется |
1,35 |
По критерию D-W положительная автокорреляция присутствует. 3 условие Cov( =0 нарушается |
Если d(расч)>2, то преобразуют по формуле d(расч)=4-d(расч), при наличии отриц.корр. Если же не определен, то в частности, можно воспользоваться первым коэффициентом автокорреляции. Если r1расч>r1табл, то гипотеза об отсутствии автокорреляции может быть принята |
||||||||||||
d1 табл = 1,08 d2 табл = 1,36 r1 табл = 0,36 (для n<15)
|
|
0,38 |
4,7 |
0,4 |
0,3 |
d1=1,08 d2=1,36 |
|||||||||||||||||
2.5 |
Средняя относительная ошибка |
Е = |
0,36 |
модель построена с приемлемой точностью |
0,32 |
модель построена с приемлемой точностью |
0,36 |
модель построена с приемлемой точностью |
0,3 |
модель построена с приемлемой точностью |
Если Еотн<15%, то считается, что модель построена с приемлемой точностью |
||||||||||||
|
Вывод |
|
МОДЕЛЬ АДЕКВАТНА ПО ДАННЫМ ПОКАЗАТЕЛЯМ |
МОДЕЛЬ НЕ АДЕКВАТНА ПО ДАННЫМ ПОКАЗАТЕЛЯМ |
МОДЕЛЬ АДЕКВАТНА ПО ДАННЫМ ПОКАЗАТЕЛЯМ |
МОДЕЛЬ НЕ АДЕКВАТНА ПО ДАННЫМ ПОКАЗАТЕЛЯМ |
|
||||||||||||||||

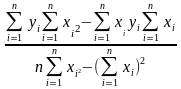
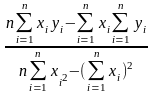
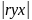 >0,7
– сильная
связь
>0,7
– сильная
связь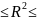 1,
чем ближе R2
к 1, тем лучше качество подгонки
1,
чем ближе R2
к 1, тем лучше качество подгонки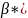 Sy
при
изменении x
на Sx
Sy
при
изменении x
на Sx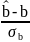 =
=
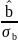
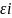 )=0
(с помощью t-критерия
Стьюдента)
)=0
(с помощью t-критерия
Стьюдента)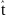 расч
=
расч
=
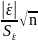
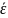 =
=
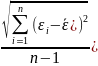
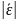 =
=
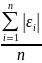
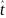 (табл)=2,2621
(табл)=2,2621 (с помощью F-критерия
Фишера)
(с помощью F-критерия
Фишера)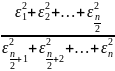
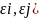 =0
(c
помощью d-критерия
Дарвина Уотсона (D-W))
=0
(c
помощью d-критерия
Дарвина Уотсона (D-W))