ЛЕКЦИЯ 5(А)

ВЫБОР ИНФОРМАТИВНЫХ ПРИЗНАКОВ.

КРИТЕРИИ И МЕТОДЫ

В этой лекции будут рассмотрены критерии для изменения эффективности признаков. Сначала, мы будем иметь дело с признаками объектов, характеризующихся одним распределением и измерять эффективность признаков с помощью собственных значений и собственных векторов. Затем, мы обобщим эти результаты на случай двух или большего числа классов, а эффективность признаков будет оцениваться с точки зрения разделимости классов.

СЛУЧАЙ ОДНОГО РАСПРЕДЕЛЕНИЯ.

Рассмотрим в начале выбор признаков в случае одного распределения. При наличии только одного распределения нельзя говорить о разделимости классов, т. е. о задаче распознавания образов. Вместо этого, мы рассмотрим, насколько точно можно описать объекты с помощью набора признаков. Если с помощью небольшого числа признаков удается точно описать объекты, такие признаки эффективны. Хотя эта задача непосредственно не связана с распознаванием образов, знание характеристик отдельных распределений помогает отделить одно распределение от других. Кроме того, выбор признаков для случая одного распределения находит широкое применение в других областях, таких как представление сигналов и сжатие данных.

Критерий минимума среднеквадратической ошибки.

Пусть - n-мерный случайный вектор. Тогда можно точно представить разложением

где (2)

(3)

Матрица - детерминированная и состоит из n-линейно-независимых векторов-столбцов. Столбцы матрицы - базисные векторы. Если условие ортонормированности выполнено, то компоненты вектора определяются следующим образом:

i=1,..n

Каждая компонента является признаком, который вносит вклад в представление наблюдаемого вектора .

Предположим, что мы определили только m (m<<n) компонент вектора и всё ещё хотим оценить . Это можно сделать, заменив заранее выбранными константами те компоненты , которые мы не вычисляем, и получить следующую оценку:

Без ограничений общности, можно сказать, что вычисляются только первые m компонент вектора y. Если используются не все признаки, то вектор представляется с ошибкой

Использую среднюю величину квадрата в качестве критерия для измерения эффективности подмножества, состоящего из m признаков:

Каждому набору базисных векторов и значений констант соответствует некоторое значение . Выберем их таким образом, чтобы минимизировать .

Оптимальный выбор констант:

Другими словами, мы должны заменить те , которые не измеряются, их математическими ожиданиями:

Тогда среднеквадратичная ошибка:

где - ковариационная матрица случайного вектора .

Оптимальный выбор матрицы :

т.е. оптимальные базисные векторы – это собственные векторы ковариационной матрицы . Т.о. , минимальная среднеквадратичная ошибка:

Разложение случайного вектора по собственным векторам ковариационной матрицы представляет собой дискретный вариант разложения Карунена – Лоева.

В задачах распознавания образов коэффициенты этого разложения рассматриваются как признаки, представляющие наблюдаемый вектор . Эффективность каждого признака, т.е. его полезность с точки зрения представления , определяется соответствующим собственным значением. Если некоторый признак исключается из разложения, то СКО увеличивается на . Поэтому, если мы хотим уменьшить число признаков, признак с наименьшим собственным значением следует исключить в первую очередь и т.д.

При разложении Карунена – Лоева мв решаем вопрос о включении или не включении в разложение собственного вектора в зависимости от величины соответствующего собственного значения. Однако абсолютная величина собственного значения не даёт ещё адекватной информации для принятия решения. Отношение собственного значения к сумме всех собственных значений показывает, какая доля среднеквадратичной ошибки вносится исключением соответствующего собственного вектора.

- можно использовать в качестве критерия

для включения или не включения в разложение i-ого собственного вектора.

Критерий разброса.

Критерий разброса представляет собой математическое ожидание квадрата расстояния между объектами:

где , - взаимно-независимые векторы-столбцы, взятые из одного распределения. Тогда

где S и - автокорреляционная и ковариационная матрицы, M – вектор математического ожидания распределения. Пусть вектор Y связан с вектором X ортогональным преобразованием

Если рассматривать только m (m<<n) компонент вектора Y, то их разброс

Теперь задачу выбора признаков можно сформулировать как задачу выбора ортонормированных векторов , максимизирующих , но должны быть доминирующими собственными векторами ковариационной матрицы .

Энтропия совокупности.

Энтропию совокупности можно использовать в качестве меры «неравномерности» распределения. Энтропия вычисляется по формуле

Если компоненты вектора X независимы, энтропию можно представить в виде суммы отдельных переменных:

Энтропия является значительно более сложным критерием, чем два предыдущих, потому что в формулу для энтропии входит плотность вероятности вектора X. И в данном случае задача выбора признаков состоит в нахождении признаков, максимизирующих для данного m (m<<n).

ВЫБОР ПРИЗНАКОВ В СЛУЧАЕ МНОГИХ РАСПРЕДЕЛЕНИЙ

При наличии двух или большего числа классов цель выбора признаков состоит в выборе таких признаков, которые являются наиболее эффективными с точки зрения разделимости классов.

С теоретической точки зрения, вероятность ошибки является наилучшим критерием эффективности признаков. Кроме того, на практике одним из более распространенных критериев является вероятность ошибки , полученная экспериментально; а именно, интуитивно выбрав набор признаков, строят классификатор и экспериментально подсчитывают число ошибок классификатора. Эта процедура является гибкой, не зависит от вида распределения и теоретически позволяет найти оптимальное решение.

Главный недостаток критерия вероятности ошибки – за исключением небольшого числа частных случаев, для него не существует явного математического выражения.

Если критерий непосредственно не связан с вероятностью ошибки, то рассматривается не сама вероятность, а её верхняя и нижняя границы.

Критерий разделимости двух классов записывается в виде:

,

где l случайных величин используются в качестве признаков. Кроме того, предположим, что лучшей разделимости классов соответствует большее значение критерия.

Дивергенция.

Дивергенция представляет собой меру разделимости классов.

В распознавании образов одной из ключевых характеристик является отношение правдоподобия:

,

где и - плотности вероятностей классов и . Поэтому, если бы мы имели возможность оценить плотности или функции распределения для классов и , это было бы почти эквивалентно оценивания вероятности ошибки. Простейший вариант – использовать математическое ожидание отношения правдоподобия для классов и и оценить разделимость классов по разности математических ожиданий. Таким образом, дивергенция:

.

Рис.1 иллюстрирует это определение. Т. к. при вычислении дивергенции рассматриваются только математические ожидания, нельзя ожидать близкой связи между дивергенцией и вероятностью ошибки. Более близкую связь можно получить, включив в выражение для дивергенции моменты более высокого порядка, но в этом случае критерий становится очень сложным.

Если плотности , , нормальны, то выражение для дивергенции принимает вид:

. (***)

Если ковариационные матрицы одинаковы, т.е. , то

.

Дивергенция в случае равных ковариационных матриц однозначно связана с вероятностью ошибки.

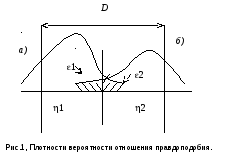
Выражение для верхней границы вероятности ошибки в зависимости от дивергенции неизвестно. Но для данного значения дивергенции вероятность правильного распознавания находится между двумя показанными на рисунке кривыми. Верхняя кривая показывает зависимость между вероятностью правильного распознавания и дивергенцией для случая многомерного распределения при равных ковариационных матрицах. Нижняя кривая – туже зависимость для одномерного случая.

Процедура выбора признаков с использованием дивергенции заключается в следующем:

1. Для первого члена (***) оптимальный признак определяется следующим образом:

Этот единственный признак является достаточным. Первый член представляет собой дивергенцию, обусловленную различием средних значений.

2. Второй член представляет собой дивергенцию, обусловленную различием ковариационных матриц, а оптимальными признаками являются собственные векторы матрицы . Наиболее важные m признаков определяются путем упорядочивания собственных значений:

3. Если требуется найти оптимальные признаки, то приходится использовать численные методы поиска или следующие процедуры:

а) Можно взять в качестве приближенно оптимальных признаков признаки для второго члена, т. е. собственные векторы матрицы , в надежде, что первый член D можно выразить небольшим числом этих признаков. Выбор признаков производится в следующем порядке:

,

где , . Если таким образом выбраны m признаков, то

.

б) Если доминирующим является первый член D, то собственный вектор - наиболее эффективный признак. Поэтому сначала выбирают , а остальные m-1 выбирают из числа признаков для второго члена D.