3. Методы линейного предсказания в задачах обработки речевых сигналов

Линейное предсказание является одним из наиболее эффективных методов анализа речевого сигнала. Этот метод является доминирующим при оценке основных параметров речевого сигнала, таких, как, например период основного тона, форманты, спектр, функция площади речевого тракта, а также при сокращенном представлении речи с целью ее передачи и хранения. Важность метода обусловлена высокой точностью получаемых оценок и простотой вычислений.

Основной принцип метода линейного предсказания состоит в том, что текущий отсчет речевого сигнала можно аппроксимировать линейной комбинацией предшествующих отсчетов. Коэффициенты предсказания при этом, определяются однозначно минимизацией среднего квадрата разности между отсчетами речевого сигнала и их предсказанными значениями. Коэффициенты предсказания – это весовые коэффициенты, используемые в линейной комбинации.

Итак, линейный предсказатель с коэффициентами a_i определяется как система, на выходе которой имеется

(3.1)

В качестве модели системы используется упрощенная модель речеобразования, изображенная на рисунке 2.2. Для линейного предсказания эта модель является наиболее полной. Передаточную функцию, используемого в этой модели линейного фильтра можно записать как

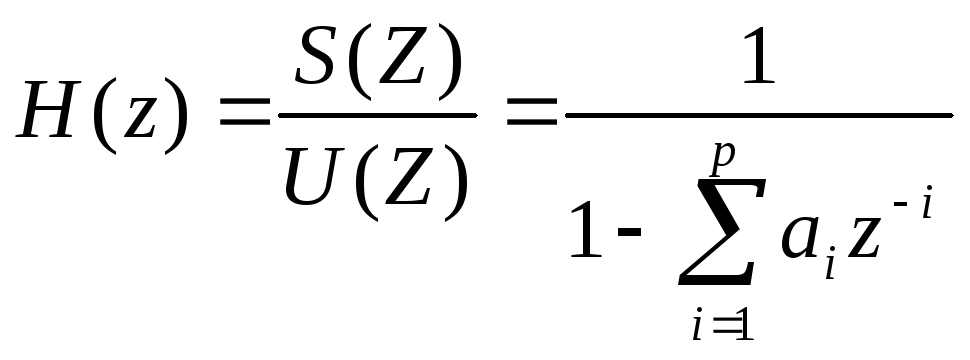(3.2)

Определение периода основного тона и классификация тон/шум могут быть осуществлены на основе использования ряда методов. Для вокализированных звуков хорошо подходит модель, содержащая только полюсы (чисто полюсная) в своей передаточной функции, но для носовых и фрикативных звуков требуется учитывать еще и нули. Однако из дальнейшего будет ясно, что если порядок p модели достаточно велик, то полюсная модель позволяет получить достаточно точное описание почти для всех звуков речи. Главное достоинство этой модели заключается в том, что как параметр G, так и коэффициенты можно оценить непосредственно с использованием очень эффективных с вычислительной точки зрения алгоритмов.

3.1. Параметрическое оценивание

Ошибка предсказателя в любой момент времени может быть представлена как

(3.3)

Вычислим квадратичную ошибку над конечным окном длины N.

(3.4)

Минимум, E, получается, когда производная равна нулю по каждому параметру, a_k.. Как можно видеть из выражения (3.4), значение E квадратично по каждому из a_k, поэтому решение единственно. Очень большие значения a_k могут привести к неправильному предсказанию и, следовательно, решение при E/a_k=0 должно быть минимумом.

Рисунок 3.1.Схема, показывающая единственность минимума квадратичной функции.

Следовательно, продифференцировав выражение (3.4) по a_j и приравняв к нулю, мы получим множество из p выражений:

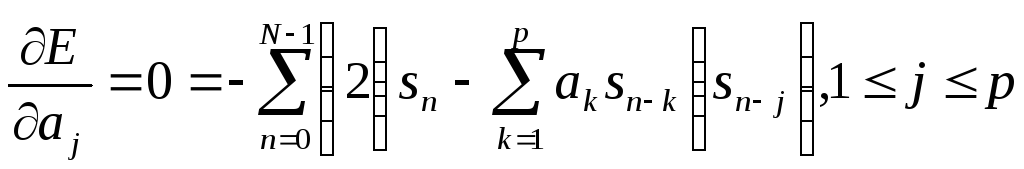(3.5)

Переписав по-другому выражение (3.5) получим:

(3.6)

Определим ковариационную матрицу Ф с элементами _i,k :

(3.7)

Теперь можно записать выражение (3.6) как:

(3.8)

или в матричной форме:

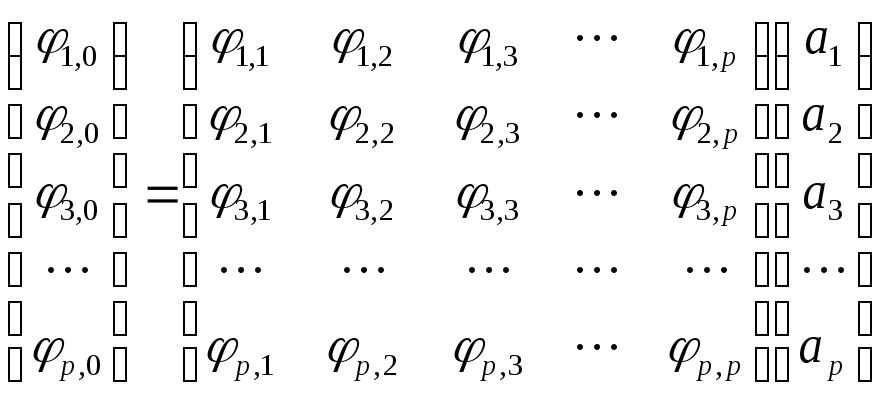(3.9)

или просто

Ф₀ = Фа (3.10)

Таким образом, путем обращения матриц получаем Ковариационный Метод а = Ф^-1Ф₀ (3.11)

Следует заметить, что Ф – симметрична, то есть _i,k = _i,k и эта симметрия может быть использована при обращении Ф.

В этих выражениях ссылаются на отсчеты s_-p,...,s_-1.

Уравнения ковариационного метода решаются на основе разложения Холецкого, более подробно данный алгоритм описан в [1].

3.2. Автокорреляционный метод.

Когда при обработке речи мы имеем дело с окнами, нам следует принять во внимание граничный эффект, чтобы избежать больших ошибок предсказания на концах. Можно переработать область, в которой мы производим конечную минимизацию квадрата, в выражении (3.4), и воспользовавшись тем фактом, что отсчеты за пределами окна равны нулю, переписать _i,j как:

(3.12)

Теперь _i,j зависит только от разности i – j, и может быть записано в терминах автокорреляционной функции _i,j = r_i-j:

(3.13)

Таким образом, Ф представляет собой матрицу Теплица:

(3.14)

Существует много методов обращения таких матриц, один из которых алгоритм рекурсии Левинсона-Дарбина. Обозначим значение LP параметров на итерации i через a_k⁽ⁱ⁾ , а оставшуюся энергию через E⁽ⁱ⁾ (E⁽⁰⁾=r₀) i = 1, 2, ...

(3.15)

(3.16)

(3.17)

(3.18)

Уравнения решаются рекурсивно для i=1,2,…,p и окончательное решение принимет вид

Параметры k_i известны как параметры отражения. Заметьте, что:

• При вычислении параметров для модели порядка p, вычисляются все промежуточные параметры для предсказателей меньших порядков

• Метод также позволяет получить коэффициенты отражения

• Результирующий фильтр – гарантированно устойчив

• Значение квадрата остатка предсказания, E⁽ⁱ⁾, также вычисляется и уменьшается (или остается константой) на каждом шаге.

Также в процессе работы алгоритма можно получить так называемые b-параметры, котрые вычисляются по формулам:

(3.19)

(3.20)

3.3. Вычисление коэффициента усиления модели.

Алгоритм Дарбина позволяет вычислить коэффициент усиления как

Также он может быть вычислен как:

(3.21)

• мощность потока импульсов, составленного из N отсчетов равна 1/N.

• Мощность переменной, имеющей Гауссовское распределение со средним 0 и единичной дисперсией.

• Мощность случайной величины, равномерно распределенной на [-1, 1] будет

(3.22)

3.4. Реализация на основе решетчатого фильтра.

Непосредственная реализация на основе БИХ фильтра может привести к нестационарности полученной системы, если a_i квантировано. Фильтр будет устойчивым, если –1 < k_i < 1 i – следовательно, k_i может быть квантировано и результат будет гарантировано устойчивым. Возможны оба пути: как переход от k_i к a_i, так и непосредственная реализация БИХ фильтра с использованием значений k_i - полезно при работе над DSP чипом ограниченной точности (как в мобильных телефонах стандарта GSM).

Здесь имеются аналоги с моделью из труб без потерь

• Каждая секция фильтра – одна секция трубы

• Впереди идущая волна частично отражается назад

• Сзади идущая волна частично отражается вперед

Следовательно подходит терминология коэффициентов отражения k_i.

Рисунок 3.2.Решетчатый фильтр

3.5. Мера Итакура.

Рассмотрим случай, когда речевой сигнал s_n пропущен через линейный предсказатель, a, соответствующие коэффициенты. Остаточная средне-квадратичная ошибка, E, может быть вычислена как:

(3.23)

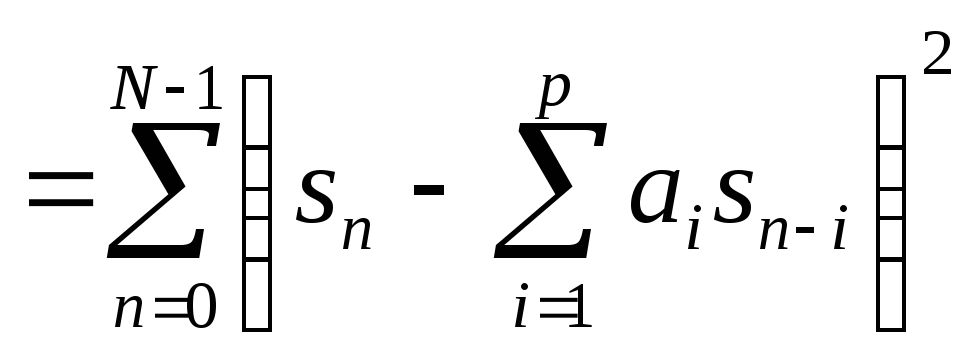(3.24)

(3.25)

(3.26)

(3.27)

(3.28)

Таким образом, можно определить:

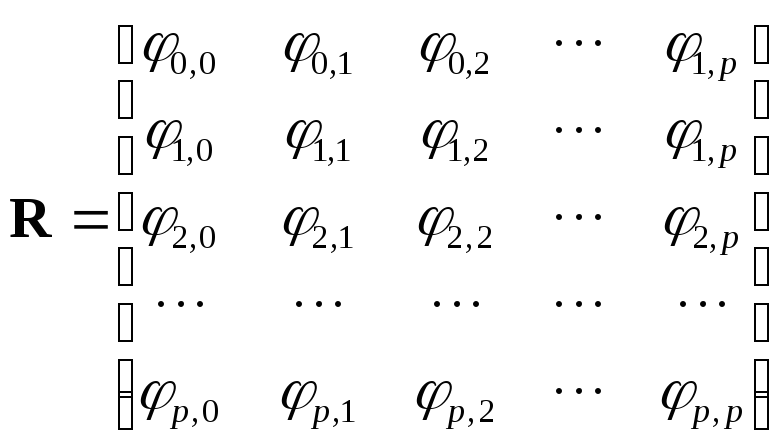(3.29)

или, что то же самое, в терминах автокорреляций:

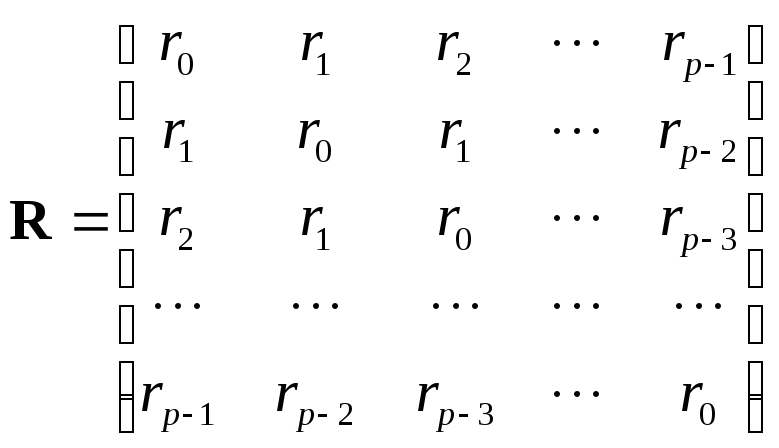(3.30)

Пусть y будет присоединенный вектор из “коэффициентов” или “ссылок” коэффициентов линейного предсказания [-1 a₁ a₂ ... a_p ], и x – присоединенный вектор из “наблюдаемых” или “неизвестных” коэффициентов линейного предсказания [-1 a’₁ a’₂ ... a’_p ]. Тогда можно вычислить следующие величины:

X R x^T = энергия на выходе инверсного фильтра, сформированная путем ссылки на входной речевой сигнал. (3.31)

y R y^T = Минимальная возможная выходная энергия из фильтра линейного предсказания с данным входным речевым сигналом. (3.32)

В автокорреляционном случае это может быть вычислено с использованием теми же комплексных Евклидовых расстояний.

(3.33)

(3.34)

3.6. Кепстр линейного предсказания

Параметры кепстра сигнала могут быть вычислены непосредственно из параметров линейного предсказания с использованием следующего рекурсивного алгоритма:

(3.35)

3.7. Логарифм отношения площадей.

Отношение площадей, A_i, в секциях в трубах без потерь может быть непосредственно вычислено из отношения коэффициентов:

(3.36)

Следовательно, предположив постоянство площадей в голосовой щели, общие перекрывающиеся секции в вокальной дорожке могут быть вычислены:

• Этот метод подчинен всем предположениям линейного предсказания.

• Нужно применить лучшие методы нормализации, чтобы сделать различимыми пересекающиеся секции.

• Эти методы могут использоваться во многих приложениях – например, для помощи глухим.

• В качестве альтернативы этот метод может дать отношения коэффициентов при известных площадях.

3.8. Корни полинома предсказания.

Знаменатель передаточной функции фильтра (см. модель речеобразования и выражение (3.2.)) может быть факторизован:

(3.37)

Где, c_k, множество комплексных чисел, определяющие корни полинома с использованием угловой частоты:

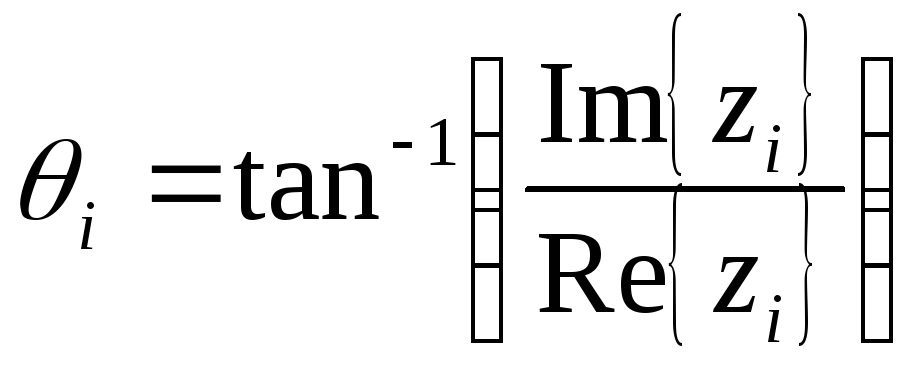(3.38)

и амплитудой:

(3.39)

Если корни замкнуты внутри единичного круга, то они представляют собой форманту.

Полином линейного предсказания может быть разложен на:

(3.40)

(3.41)

Теперь:

• Все корни P(z) и Q(z) лежат внутри единичного круга.

• Все корни P(z) и Q(z) – рассеяны

• P(z) соответствует голосовому тракту при закрытой голосовой щели, а Q(z) при открытой.

• Очень полезно при кодировании речевых сигналов.

После того, как в главах 2,3 был описан процесс предварительно обработки речевого сигнала можно переходить к распознаванию с использованием полученных признаков.

4. Разработка алгоритма распознавания речевых