14

Глава «КРАТНЫЕ ИНТЕГРАЛЫ». 1

§1 Кратные интегралы : определение, свойства. 1

§2 Вычисление двойного интеграла в прямоугольных координатах. 3

§3 Вычисление двойного интеграла в полярных координатах; обобщенные полярные координаты. 5

§4 Вычисление тройных интегралов. 9

§5 Замена переменных в двойном и в тройном интегралах 12

Глава «КРАТНЫЕ ИНТЕГРАЛЫ».

§1 Кратные интегралы : определение, свойства.

Пусть в области D задана непрерывная скалярная функция n переменных:

n=1 | n=2 | n=3

1)Введем произвольное разбиение области D на “ячейки”σ_i без пропусков и наложений ; выберемпроизвольно точку A_i€σ_i; обозначим : Δσ_i «меру ячейки» (Δx_i – длина отрезка; ΔS_i – площадь σ_i ; ΔV_i – объем σ_i); d=max{ d_i } - “диаметр разбиения” , d_i – ”диаметр ячейки” - наибольший линейный размер ячейки; m,M – наименьшее и наибольшее значения функции в области D .

2) Назовем множество P_n={σ_i; A_i; i=1,..,n} разбиением с отмеченными точками и составим сумму S_n(P_n,f)=.

Определение 1.

1.1 Сумма произведений значений функции в отмеченных точках на меру ячейки разбиения называется “интегральной суммой” для функции f при разбиении P_n области D.

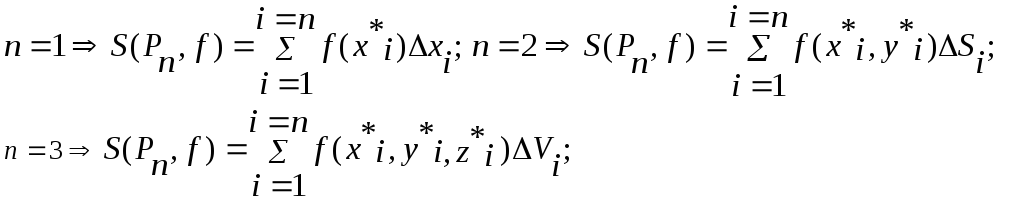
2. Сумма произведений меры ячейки разбиения на наименьшее (наибольшее) значение функции в ячейке называется нижней L_n (верхней U_n) суммой Дарбу:

Определение 2.

Если существует конечный предел интегральных сумм при измельчении разбиений 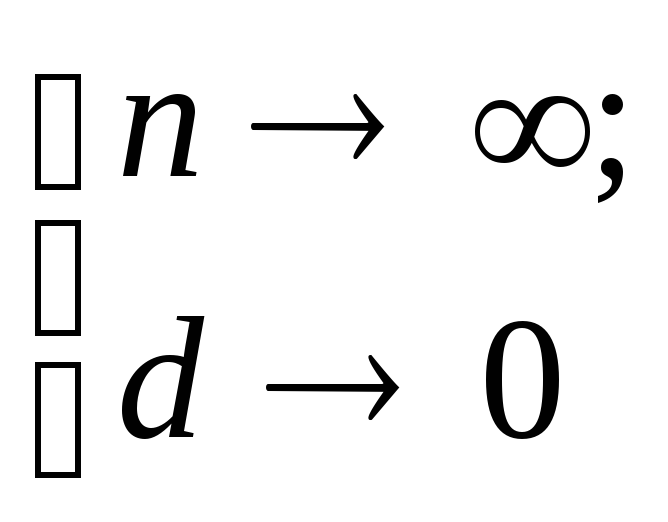, (который не зависит ни от разбиений ни от выбора отмеченных точек) его называютинтегралом от функции f по области D и пишут

Свойства интеграла

1. Аддитивность - - интеграл по объединению областей равен сумме интегралов по каждой части области.

2. Линейность - 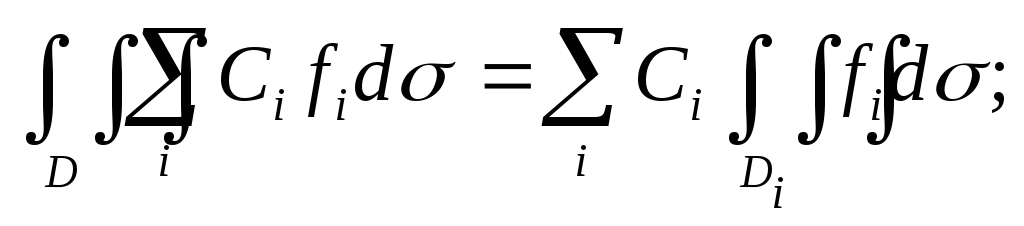- интеграл от линейной комбинации функций равен линейной комбинации интегралов.

3. Геометрическая иллюстрация

4. Оценки интеграла для непрерывной функции f:

Теорема (существования).

Функция многих переменных, непрерывная в области D, интегрируема в ней.

§2 Вычисление двойного интеграла в прямоугольных координатах.

По определению:

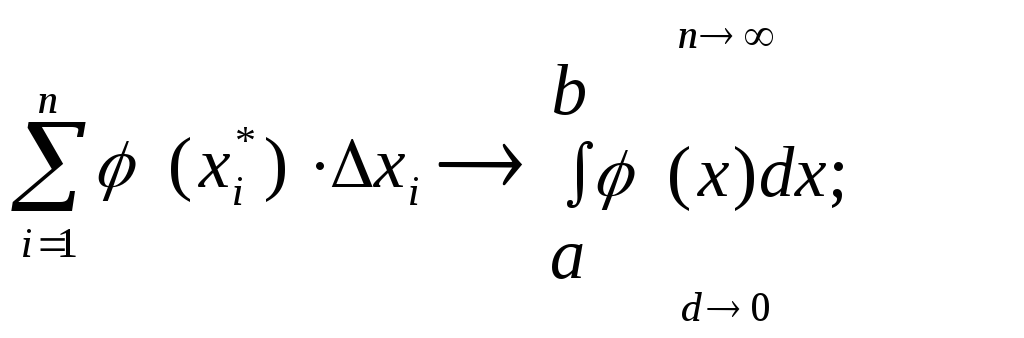
Пусть область интегрирования D ограничена на промежутке x€[a,b] линией у=у_н(х) снизу и линией у=у_В(х) сверху. Пользуясь «свободой» разбиения и выбора отмеченных точек области,

-введем разбиение области вертикальными и горизонтальными линиями прямоугольной координатной сетки - прямымиy=y_j=const, x=x_i=const на прямоугольные ячейки площадью и

- внутри каждого вертикального «столбика» x_i<x<x_i+1 выберем отмеченные точки с одинаковыми абсциссами :x=x_i^*.

x_i

x_i+1

- упорядочим суммирование в интегральной сумме

Несложно заметить, что внутренняя сумма представляет интегральную сумму для интеграла от функции одной переменной - сужения функции f на прямую x=x_i^*, так что После этого, внешняя сумма так же представляетинтегральную сумму для интеграла от функции одной переменной F(x), так что

При другом «порядке интегрирования»

Таким образом, вычисление двойного интеграла сводится к двукратному интегрированию функций одной переменной, причем

(1) внутреннее интегрирование функции одной переменной (сужения функции f на координатную линию: x=const || OY  g(y)=f(x,y) или y=const ||OXg(x)=f(x,y) ); выполняется вдоль отрезка или, переменные границы которого – уравнения линий, ограничивающих областьD СНИЗУ и СВЕРХУ или СЛЕВА и СПРАВА;

(2) повторное интегрирование (внешний интеграл) функции одной переменной выполняется по отрезку x€[a;b] или y€[c;d], где a,b и c,d - являются наименьшее и наибольшее значения “второй” переменной во всей области интегрирования D.

Замечание. Если при выбранном порядке интегрирования границы области вдоль соответствующей координатной прямой задаются различными уравнениями (“сложная область”), область интегрирования следует разбить на “простые части”.

--------------------------------------------------------------------------

Задание «Двойной интеграл»: «1. Восстановить область интегрирования D двойного интеграла, записанного в виде двукратного интеграла; 2. изменить «порядок интегрирования» в прямоугольных координатах и 3. записать двойной интеграл в полярных координатах».

1. Из свойства аддитивности интеграла следует, что

Область D₁ принадлежит полосе и ограничена СНИЗУ линиейy_H≡0 и СВЕРХУ – линией y_B(x)=1-x.

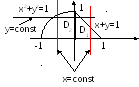Область D₂ принадлежит полосе и ограничена СНИЗУ линиейy_H≡0 и СВЕРХУ – линией y_B(x)=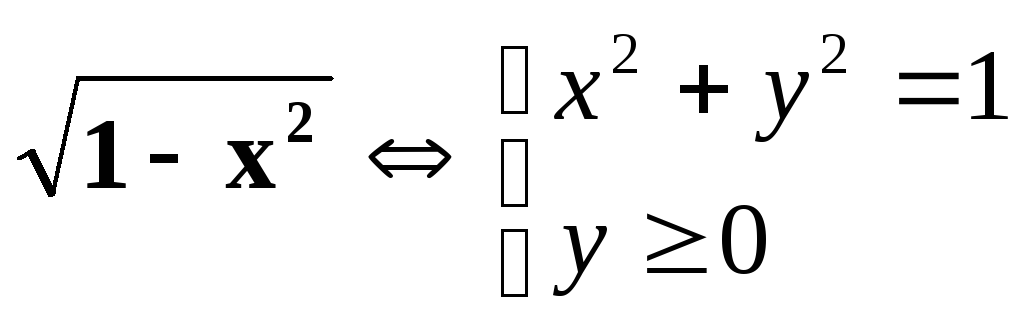-(верхняя полуокружность).

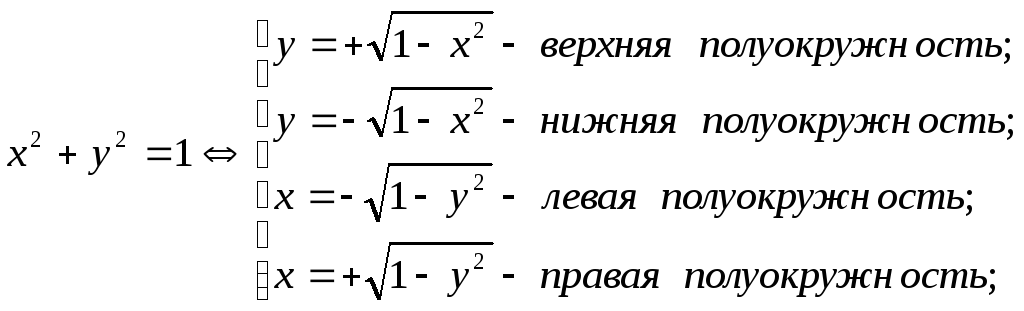
2. При другом порядке интегрирования:

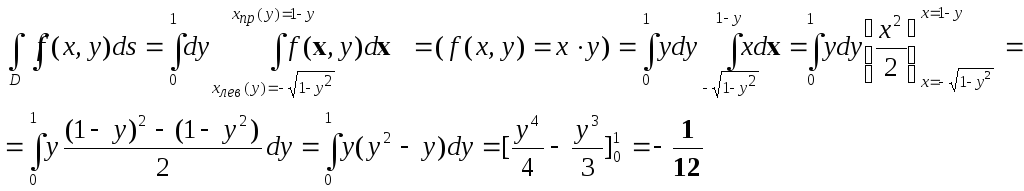
(в) Так как вдоль линии y=const граница области D «справа» задается двумя различными уравнениями , запишем интеграл как сумму двух интегралов