Лабораторная работа 31 / Lab3

Кафедра МО ЭВМ

ОТЧЕТ

по лабораторной работе № 3 по дисциплине

"Методы оптимизации"

“ Симплексный метод ”

Выполнили: Воробьёв А.В.

Ламеров Д.Ю.

Швецов М.Н.

Шефер Е.В.

Факультет КТИ

Группа № 4352

Проверил Балтрашевич В.Э.

«Выполнено» «____» _______ ____

Подпись преподавателя __ _

Санкт-Петербург

2006

Цель работы. Изучение симплексного метода решения задач ли­нейного программирования.

Постановка задачи

Рассматривается следующая задача, получившая название задачи линейного программирования.

Найти минимум линейной функции ƒ n аргументов:

ƒ = c₁x₁ + c₂x₂ + ... + c_nx_n,

где С_i - постоянные коэффициенты, на множестве, заданном набором линейных ограничений:

α₁₁x₁ + α₁₂x₂ + ... + α_1nx_n ≥ B₁

...

α_m1x₁ + α_m2x₂ + ... + α_mnx_n ≥ B_m

x₁ ≥ 0, ..., x_n ≥ 0,

где α_ij, B_i - постоянные коэффициенты.

Пусть А = - m*n - матрица, а

- векторы,

тогда ограничения записываются следующим образом:

где неравенства понимаются покоординатно.

Целевая функция ƒ может быть представлена в виде скалярного

произведения ƒ = (C, X).

Множество называется допустимым Х-многогранником.

Оптимальной точкой задачи линейного программирования называет­ся такая точка X*, что и (C, X*) ≤ (C, X) для всех . Известно, что среди оптимальных точек содержится хотя бы одна крайняя точка X.

Описание метода

Симплексный метод решения задач линейного программирования состоит из двух этапов:

1) поиск крайней точки допустимого множества,

2) поиск оптимальной точки путём направленного перебора край­них точек.

Преобразуем ограничения Ax ≥ B к виду Y = Ax – B ≥ 0

Графический способ решения задачи симплексным методом связан

с таблицей:

	X1	X2	...	Xn	B
Y1	α11	α12	...	α1n	B1
Y2	α21	α22	...	α2n	B2
...	...	...	...	...	...
Ym	αm1	αm2	...	αmn	Bm
	C1	C2	...	Cn	ƒ(X)

Крайняя точка найдена, если все элементы вектора-столбца В боль- ше нуля. Крайняя точка не существует, если в таблице существует строка, все элементы которой неположительны, а последний элемент -отрицательный.

Чтобы найти крайнюю точку надо:

1) выбрать строку i, в которой В[i] < О;

2) выбрать столбец S, в котором A[i, S] ≥ 0;

3) в столбце S задать номер строки r разрешающего элемента так, чтобы отрицательное отношение B[r]/A[r, S] было максималь-ным.

4) поменять местами имена координат в таблице из строки r и столбца S.

5) рассматривая элемент A[r, S] как разрешающий, необходимо преобразовать таблицу по формулам

ARS := A[r, s];

Z1[r, S] := 1 / ARS;

Z1[r, j] := -Z[r, j] / ARS, j ≠ S;

Z1[i, S] := Z[i, S] / ARS, i ≠ r;

Z1[i, j] := (Z[i, j] * ARS – Z[i, S] * Z[r, j]) / ARS,

i ≠ r, j ≠ S;

Z := Z1,

где под Z и Z1 понимается соответственно первоначальное и пре­образованное значение таблицы (кроме левого столбца и верхней строки).

Оптимальная, точка найдена, если все элементы вектор-строки С ≥ О (при этом все элементы вектор-столбца B ≥ 0).

Оптимальная точка не существует, если в таблице есть стол­- бец j, в котором С[j] < 0, а все A[i, j] > 0 при .

Чтобы найти оптимальную точку, надо:

1) выбрать столбец S, в котором C[S] < 0;

2) в столбце S задать номер строки r разрешающего элемен- ­та так, чтобы отрицательное отношение B[r] / A[r, S] было макси­мальным.

3) поменять местами в таблице имена координат из строки r и столбца S.

4) преобразовать таблицу по формулам (3.1).

Координаты оптимальной точки определяются следующим образом:

1) если X[j] находится на i -м месте левого столбца, то его значение равно B[i];

2) если X[i] находится на j -м месте верхней строки, то его значение равно 0.

Исследование метода

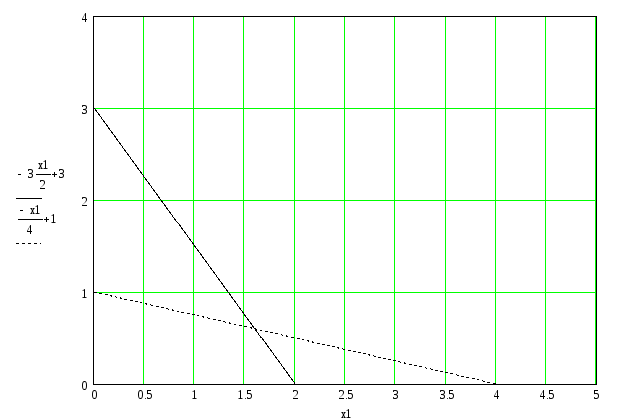
Вариант 1

Дано:

целевая функция:

f = x1 + x2;

ограничения:

y1: 3x1 + 2x2 – 6 ≥ 0;

y2: x1 + 4x2 – 4 ≥ 0;

Шаг 1:

| x1 x2 | b[i]

----------------------------

y1 | 3.00 2.00| -6.00

y2 | 1.00 4.00| -4.00

----------------------------

c[j]| 1.00 1.00| 0.00

Шаг 2:

| y1 x2 | b[i]

----------------------------

x1 | 0.33 -0.67| 2.00

y2 | 0.33 3.33| -2.00

----------------------------

c[j]| 0.33 0.33| 2.00

Шаг 3:

| y2 x2 | b[i]

----------------------------

x1 | 1.00 -4.00| 4.00

y1 | 3.00 -10.00| 6.00

----------------------------

c[j]| 1.00 -3.00| 4.00

Шаг 4:

| y2 y1 | b[i]

----------------------------

x1 | -0.20 0.40| 1.60

x2 | 0.30 -0.10| 0.60

----------------------------

c[j]| 0.10 0.30| 2.20

Координаты оптимальной точки:

x1= 1.60

x2= 0.60

Вариант 2

Дано:

целевая функция:

f = -x2;

ограничения:

y1: 2x1 - x2 + 1 ≥ 0;

y2: x1 - 2x2 + 5 ≥ 0;

y3: -x1 - x2 + 7 ≥ 0;

y4: -x1 + x2 + 3 ≥ 0;

Шаг 1:

| x1 x2 | b[i]

----------------------------

y1 | 2.00 -1.00| 1.00

y2 | 1.00 -2.00| 5.00

y3 | -1.00 -1.00| 7.00

y4 | -1.00 1.00| 3.00

----------------------------

c[j]| 0.00 -1.00| 0.00

Шаг 2:

| x1 y1 | b[i]

----------------------------

x2 | 2.00 -1.00| 1.00

y2 | -3.00 2.00| 3.00

y3 | -3.00 1.00| 6.00

y4 | 1.00 -1.00| 4.00

----------------------------

c[j]| -2.00 1.00| -1.00

Шаг 3:

| y2 y1 | b[i]

----------------------------

x2 | -0.67 0.33| 3.00

x1 | -0.33 0.67| 1.00

y3 | 1.00 -1.00| 3.00

y4 | -0.33 -0.33| 5.00

----------------------------

c[j]| 0.67 -0.33| -3.00

Шаг 4:

| y2 y3 | b[i]

----------------------------

x2 | -0.33 -0.33| 4.00

x1 | 0.33 -0.67| 3.00

y1 | 1.00 -1.00| 3.00

y4 | -0.67 0.33| 4.00

----------------------------

c[j]| 0.33 0.33| -4.00

Координаты оптимальной точки:

x1= 3.00

x2= 4.00

Вариант 3

Дано:

целевая функция:

f = 2x1 + 3x2;

ограничения:

y1: 3x1 + 2x2 - 6 ≥ 0;

y2: x1 - 2x2 - 4 ≥ 0;

Шаг 1:

| x1 x2 | b[i]

----------------------------

y1 | 3.00 2.00| -6.00

y2 | 1.00 -2.00| -4.00

----------------------------

c[j]| 2.00 3.00| 0.00

Шаг 2:

| y1 x2 | b[i]

----------------------------

x1 | 0.33 -0.67| 2.00

y2 | 0.33 -2.67| -2.00

----------------------------

c[j]| 0.67 1.67| 4.00

Шаг 3:

| y2 x2 | b[i]

----------------------------

x1 | 1.00 2.00| 4.00

y1 | 3.00 8.00| 6.00

----------------------------

c[j]| 2.00 7.00| 8.00

Координаты оптимальной точки:

x1= 4.00

x2= 0.00

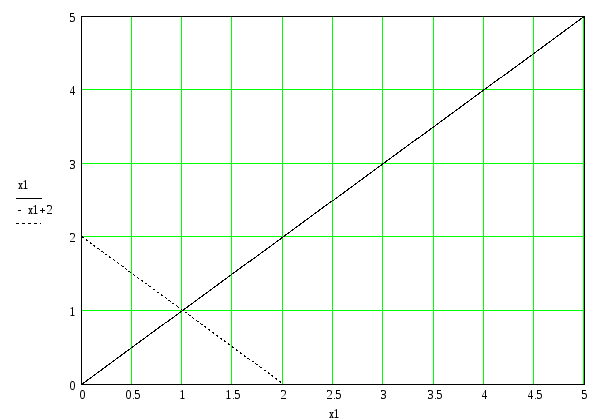
Вариант 4

Дано:

целевая функция:

f = x1 + 2x2;

ограничения:

y1: x1 - x2 ≥ 0;

y2: x1 + x2 - 2 ≥ 0;

Шаг 1:

| x1 x2 | b[i]

----------------------------

y1 | 1.00 -1.00| 0.00

y2 | 1.00 1.00| -2.00

----------------------------

c[j]| 1.00 2.00| 0.00

Шаг 2:

| y2 x2 | b[i]

----------------------------

y1 | 1.00 -2.00| 2.00

x1 | 1.00 -1.00| 2.00

----------------------------

c[j]| 1.00 1.00| 2.00

Координаты оптимальной точки:

x1= 2.00

x2= 0.00

Вариант 5

Дано:

целевая функция:

f = -x1;

ограничения:

y1: 2x1 - x2 + 2 ≥ 0;

y2: - x2 + 4 ≥ 0;

y3: -x1 - 2x2 + 12 ≥ 0;

y4: -x1 + x2 + 3 ≥ 0;

y5: x1 + x2 – 2 ≥ 0;

Шаг 1:

| x1 x2 | b[i]

----------------------------

y1 | 2.00 -1.00| 2.00

y2 | 0.00 -1.00| 4.00

y3 | -1.00 -2.00| 12.00

y4 | -1.00 1.00| 3.00

y5 | 1.00 1.00| -2.00

----------------------------

c[j]| -1.00 0.00| 0.00

Шаг 2:

| y5 x2 | b[i]

----------------------------

y1 | 2.00 -3.00| 6.00

y2 | 0.00 -1.00| 4.00

y3 | -1.00 -1.00| 10.00

y4 | -1.00 2.00| 1.00

x1 | 1.00 -1.00| 2.00

----------------------------

c[j]| -1.00 1.00| -2.00

Шаг 3:

| y4 x2 | b[i]

----------------------------

y1 | -2.00 1.00| 8.00

y2 | 0.00 -1.00| 4.00

y3 | 1.00 -3.00| 9.00

y5 | -1.00 2.00| 1.00

x1 | -1.00 1.00| 3.00

----------------------------

c[j]| 1.00 -1.00| -3.00

Шаг 4:

| y4 y3 | b[i]

----------------------------

y1 | -1.67 -0.33| 11.00

y2 | -0.33 0.33| 1.00

x2 | 0.33 -0.33| 3.00

y5 | -0.33 -0.67| 7.00

x1 | -0.67 -0.33| 6.00

----------------------------

c[j]| 0.67 0.33| -6.00

Координаты оптимальной точки: x1= 6.00 x2= 3.00