Финансовая математика / FinMath_cor3

ВВЕДЕНИЕ

В развитой экономике участники рынка интенсивно обмениваются благами, в том числе правами и обязательствами. Описание рациональных условий такого обмена – важная часть экономической теории. Предметом изучения в рассматриваемой далее теории расчетов являются стандартные обязательства (контракты), обмен которыми производится по фиксированным правилам на биржах, где встречаются покупатели и продавцы обязательств. В ходе торгов цена контракта устанавливается на уровне S , при котором число покупателей и число продавцов уравновешены (равны). Таким образом, инвестор в ходе торговой сессии может, по своему усмотрению, купить или продать нужное число контрактов по цене S .

Предположим, что торгуемый сегодня контракт f предусматривает будущую выплату держателю контракта в размере y , если в следующем году будет засуха, и в размере z , если засухи не будет. Выплата будет осуществляться за счет продавца контракта. Именно за этот будущий платеж продавец контракта получает от покупателя в настоящее время сумму C . Условимся, что y ≥ 0, z ≥ 0, и задумаемся о рациональной стоимости (ценности) C дан-

ного контракта: C = C( y, z) ≥ 0.

Если стоимость контракта при ( y = 6, z = 2), например, известна (установилась на бирже на уровне C = 3 ), то какова должна быть стоимость контракта для ( y = 5, z = 9 ) при условии, что стоимость денег за рассматриваемый период не меняется? Задачи такого рода подробно изучаются в экономической теории, начиная с первой половины семидесятых годов ХХ века. Данный пример разобрать нетрудно, учитывая, что функция C( y, z) , повидимому, линейна, и, кроме того, C(1,1) =1, поскольку бумага с выплатой f ≡1 должна стоить 1.

Таким образом, ценность C( y, z) = Fy +Gz определяется равенствами 1 F +1 G =1; 6 F + 2 G = 3; откуда F =1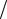4, G = 3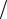4 и, окончательно

C = C( y, z) = ( y +3z)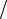4; C = C(5, 9) = 8.

Как найти ответ, если ценность денег изменяется с течением времени по известному закону? Как определить C в более сложной обстановке, когда

3

базовый актив X (в данном примере – погода) изменяется несколько раз или, например, описывается случайным процессом с непрерывным временем? Эти и другие задачи рассматриваются в курсах финансовой аналитики.

Настоящие методические указания написаны по материалам лекций начального уровня, читавшихся в разные годы студентам Электротехнического университета и Европейского университета в Санкт-Петербурге. Авторы признательны А. М. Коточигову за поддержку публикации, а также Е. А. Широковой и М. Б. Лифшиц за неизменную и терпеливую помощь при подготовке рукописи. Без их усилий работа не была бы завершена.

Предполагалось, что студенты знакомы с основными понятиями теории вероятностей и началами стохастического анализа. Минимальной подготовки требуют задания 1− 3, 5, 8, 19 − 27.

1. ИНСТРУМЕНТЫ И ЗАДАЧИ ФИНАНСОВОЙ ИНЖЕНЕРИИ

1.1. Финансовый рынок

На финансовом рынке встречаются и взаимодействуют инвесторы, корпорации (фирмы) и посреднические структуры (например, биржи). Финансовый рынок – система денежных рынков, рынков ценных металлов и иных валютных ценностей, рынков финансовых инструментов. На рынках финансовых инструментов различают основные (первичные) инструменты и производные (вторичные) инструменты, определяемые на основе первичных.

Такие (вторичные) инструменты – опционы, фьючерсные контракты и т. д. играют все возрастающую роль на финансовых рынках, начиная, примерно, с 1973 г.

Косновным инструментам относят (и в рамках финансовой теории изучают и моделируют) акции, облигации и банковские счета.

Кпроизводным финансовым инструментам относят величины, значе-

ния которых по фиксированным правилам (контрактам) точно определяются поведением основных инструментов. Расширение рынка производными инструментами открывает перед участниками рынка дополнительные возможности – в частности, возможности страхования рисков.

Основной частью финансовой теории является конструирование и изучение математических моделей поведения базовых активов, проверка соответствия рассматриваемых моделей реальной (наблюдаемой) динамике финансового рынка.

4

Задачи определения справедливой (рациональной) стоимости контрактов также являются одними из важнейших в финансовой аналитике. Методы решения этих задач существенно зависят от структуры моделей изменения базовых активов и от особенностей определения изучаемых контрактов (платежей).

1.2. Банковский счет

Банковский счет – это ценная бумага, по которой банк обязуется выплачивать ее держателю определенный процент от суммы счета.

В последнем случае говорят о непрерывно начисляемых процентах. При непрерывно начисляемых процентах с процентной ставкой ρ стартовый ка-

питал B0 через T лет превратится (по определению) в B0eρT . Таким обра-

зом, одинаковый для обоих случаев рост накоплений обеспечивается при условии, что B0eρT = B0 (1+ R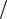k)kT , когда ρ = k ln(1+ R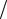k) . Важно, что ρ < R .

Задание 1

По банковскому счету A проценты начисляются один раз в квартал, годовая ставка 12 %. Какой непрерывно начисляемой ставке процента ρ отвечает счет A ?

Решение. Согласно условиям, eρT = AT = (1+0,12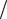4)4T . Поэтому

ρ = 4ln(1+0,03) = 0,11823K

Ответ: ρ =11,8 % .

Задание 2

По банковскому счету A проценты начисляются один раз в год, годовая ставка 16 %, по банковскому счету B проценты начисляются непрерывно, годовая ставка 15 %. Какой счет предпочтительнее?

5

B0 = A0 и второй счет предпочтительнее.

Различные ценные бумаги, как базовые, так и производные, часто сопоставляются с банковским счетом. Этим определяется важность банковского счета как основного финансового инструмента.

Рассмотренную экспоненциальную модель BT = B0 exp(ρT ) , для которой dBt = ρBt dt, часто используют для описания безрискового актива, доступного для заемщиков и кредиторов на рынках финансовых активов. В более общей ситуации (безрисковая) ставка ρ может быть переменной, тогда

t

dBt = ρt Bt dt, или, эквивалентно, BT = B0 exp ∫ρsds .

0

1.3. Базовые активы как случайные переменные

Инвесторы приобретают финансовые активы в расчете на получение в будущем определенных благ, в частности на возможный рост совокупной стоимости приобретаемых активов. Не все финансовые активы обладают одинаковой ожидаемой доходностью. Будущая стоимость большинства активов неизвестна и трудно прогнозируема. Естественной (и общеупотребительной) моделью поведения финансовой переменной является случайная функция X t , принимающая скалярные (цена одного актива) или векторные (список цен нескольких активов) значения. Основным понятиям теории случайных функций посвящена превосходная книга А. Д. Вентцеля [2].

Согласно современным представлениям, на равновесном рынке доходность актива тем больше, чем выше риски, связанные с инвестированием в актив. Описание баланса рисков и доходностей составляет предмет теории ценообразования (CAPM – Capital Asset Pricing Model) Марковица и Шарпа (см., например, [3, гл. 1]).

Случайные функции (переменные) часто называют также стохастическими (случайными) процессами, а в случае, когда время t дискретно, – стохастическими последовательностями.

Основные классы случайных переменных и их свойства рассматриваются в курсе теории случайных процессов. Для приложений в финансовой аналитике важнейшими среди них являются процессы Маркова и мартингалы.

6

Большую роль играют также гауссовские процессы и стационарные процессы, часто встречающиеся при описании установившихся режимов тех или иных стохастических систем.

Случайный процесс называется марковским, если при s < t

E{g( X t ) | Fs} = E{g( X t ) | X s}

для всех (ограниченных, измеримых) функций g или, в упрощенной и часто

используемой форме E{g( X t ) | Fs} = f ( X s ). Здесь Fs – алгебра (точнее, σ-алгебра) событий, “доступных наблюдению к моменту времени s ”. Предполагается, что с ростом s алгебры Fs только лишь расширяются, причем величины X s полностью определены событиями алгебры Fs ( X s измери-

мы относительно Fs ).

Символ условного математического ожидания E{ξ| F} = η используется для обозначения прогноза величины ξ по наблюдениям над событиями, содержащимися в F. Во многих случаях величина η может быть определена

вся информация, необходимая для оптимального прогнозирования (недоступного для наблюдения) платежа g( X t ) по результатам наблюдений над

ти к уменьшению ошибки прогноза (улучшению его качества). Записывая марковское свойство процесса X в упрощенной форме

E{g( Xt ) | Fs} = f ( X s ) ,

преобразование g a f называют оператором перехода или переходной функцией и обозначают Qst .

7

Операторы перехода линейны, положительны (прогноз неотрицательного платежа неотрицателен) и нормированы:

Qst 1 = 1

− прогноз постоянной есть сама постоянная. Кроме того, переходные функции процесса Маркова подчиняются уравнениям Чепмена−Колмогорова

Именно эти уравнения (имеющие аналогом теорему о трех перпендикулярах в евклидовой геометрии) позволяют привлечь к анализу марковских процессов и их числовых характеристик мощные средства математического анализа. Решающие достижения здесь связаны с пионерскими работами А. Н. Колмогорова 1931 г. С другой стороны, введенный А. А. Марковым класс процессов, носящих его имя, весьма богат. В него попадают как процессы с независимыми приращениями, так и многие процессы с жесткой зависимостью прошлого и будущего (например, X s ≡ X 0 или, более общим образом, X s = Yβs , где βs – неслучайные коэффициенты, βs ≠ 0 ).

Для полного описания всех числовых характеристик марковского процесса X достаточно указать в дополнение к переходным операторам Qst еще

при надлежащем определении распределения вероятностей в левой части равенства. Особенно просто приведенные соотношения выглядят, когда про-

даны стохастическими строчками (клетки неотрицательны, сумма клеток в строчке равна единице). Так же просто дело обстоит при этом с переходными

операторами Qst . Эти операторы, предназначенные для вычисления условных математических ожиданий, должны быть заданы матрицами, составленными из условных вероятностей

P{X t = j X s = i}.

8

Строчки таких матриц оказываются стохастическими, а уравнения

на−Колмогорова записывают в форме QsQt = Qs+t , где s ≥ 0, t ≥ 0 , и используют для изучения процесса свойства возникающей полугруппы операторов. Существенную роль играют инвариантные распределения π, для которых

вой) процесс g( X s ) оказывается мартингалом (см. далее) относительно Fs . Это означает, что

Укажите все гармонические функции (столбцы) такого процесса.

9

А. А. Маркова о финальных вероятностях.

Богатый класс марковских процессов составляют процессы с независимыми приращениями. Для таких процессов величины

полностью заданы, если известны начальное распределение πt0 и распреде-

ления приращений Xt − X s . Если время t дискретно, то получаются просто

суммы независимых случайных величин

X t = ∑ζ j . j≤t

Если время t изменяется непрерывно (например, t [0,∞)) , марковское свойство процесса с независимыми приращениями особенно легко объясняется для платёжных функций специального вида, а именно для функций

g(x) = exp(itx).

Такие платёжные функции ограничены, образуют богатый класс (это известно из гармонического анализа) и, кроме того, подчиняются равенству

g(x + y) = g(x) g( y).

Знаменитый пример процесса с независимыми приращениями – процесс броуновского движения – впервые описал в 1900 г. Л. Башелье и точно построил в 1923 г. Н. Винер. Процесс броуновского движения часто называют винеровским процессом и обозначают {Wt }.

10

Согласно требованиям Л. Башелье:

Wt – процесс с независимыми приращениями;

W0 = 0 ;

Wt −Ws всегда имеет нормальное (гауссовское) распределение с нулевым математическим ожиданием и дисперсией t − s .

При таких обстоятельствах процесс Ws – гауссовский (все его конечномерные распределения гауссовские), причем

EWt = 0, cov( X s , X t ) = min(s,t) .

В частности, DX t = t . Конструкция Винера обеспечивала, кроме этого, важнейшее свойство непрерывности траекторий процесса.

Как показал позднее Колмогоров, траектории (непрерывного) винеровского процесса с вероятностью 1 подчиняются на конечном временном интервале [0,T ] условию Л. Гёльдера

X s − X t ≤ A | t − s | β,

если 0 < β <1/2, и не подчиняются такому условию при β >1/2 или даже β =1/2. Более точное описание колебаний винеровской траектории связано с законом повторного логарифма Хинчина−Леви (см. [1, гл. VIII], [2, гл. 7]).

Поскольку гладкие (дифференцируемые) функции должны подчиняться условию Гёльдера с показателем β =1, следует ожидать, что свойства траекторий процесса броуновского движения – и других процессов, с ним тесно связанных, – могут существенно отличаться от привычных.

В то же время, хотя на любом конечном промежутке [a,b] винеровская траектория имеет бесконечную вариацию, величина

υ = ∑|W (t j+1) −W (t j ) | β

j

конечна с вероятностью 1 при β = 2 для любого дробления τ, образован-

стремится к нулю. Принято поэтому считать, что dυ = dt, или, с большей ус-

ловностью, (dWt )2 ≈ dt . Если же β > 2 , то, разумеется, υ → 0 , а когда β < 2 , то υ → +∞. Подробности см. в §1.2 учебника А. Д. Вентцеля [2].

11

1.4. Производящий оператор и уравнения Колмогорова для переходных вероятностей

Однородный марковский процесс с дискретным временем полностью определяется начальным распределением и оператором перехода за один шаг

Уравнения Чепмена−Колмогорова Qt+s = QtQs позволяют надеяться на

представление Qt = exp(At) . Такое представление, действительно, можно получить, когда оператор A ограничен. Примером может быть процесс Пуассона ηt , для которого

(Ag)(x) = λ(g(x +1) − g(x)).

Здесь λ – интенсивность, Eηt = λt. В других случаях определение экспоненты может быть затруднено. Для винеровского процесса оператор

Ag = 1 ∂2 g

2 ∂x2

определен на широком классе функций, хотя и не является ограниченным в пространстве ограниченных функций.

В любом случае производящий оператор A может быть использован для описания всей переходной функции однородного процесса Маркова, поскольку, как нетрудно показать, при надлежащих предположениях

AQt = ddt Qt = Qt A .

Кроме того, оператор (γI − A) является обратным к преобразованию Лапласа

∞

∫e−γtQt dt.

0

Отсюда следует, что производящий оператор должен однозначно определять переходную функцию Qt .

12