2.2. Случайные величины

Результатом опыта со случайным исходом может быть число. Так при бросании кости выпадает от 1 до 6 очков, т.е. с опытом связана случайная величина, принимающая с одинаковой вероятностью значения 1, 2, …, 6. С бросанием монеты также удобно связать случайную величину, принимающую с вероятностью значения 0 или 1. Если же монету подбросить n раз, то число выпадений герба является случайной величиной, принимающей значения от 0 до n.

Если случайная величина принимает значения т.е. конечное или счётное множество значений, то она называется дискретной случайной величиной. Закон распределения дискретной случайной величины задаётся вероятностями . При этом всегда Важнейшими дискретными случайными величинами (сл.вел.) являются:

1. бернуллиевская сл.вел., принимающая два значения 1 и 0,

, q (бросание монеты, не обязательно симметричной);

2. биномиальная сл.вел. принимающая значения 0,1,…,n,

, i=0,1,…,n (число выпадений орла в серии из n бросаний несимметричной монеты, когда вероятность выпадения орла равна р, решки- q=1-p, ).

3. пуассоновская сл.вел., принимающая значения 0,1,…,

, i=0,1,… (число телефонных звонков или щелчков счётчика Гейгера за некоторый промежуток времени, если среднее число звонков или щелчков за подобный промежуток равно ).

Наряду с дискретными встречаются и непрерывные сл.вел.. В

качестве примеров можно привести время, проведённое на остановке в ожидании автобуса, расстояние на которое прыгает спортсмен на соревнованиях по прыжкам в длину, ваш собственный вес, измеренный после лечебной диеты и т.д.

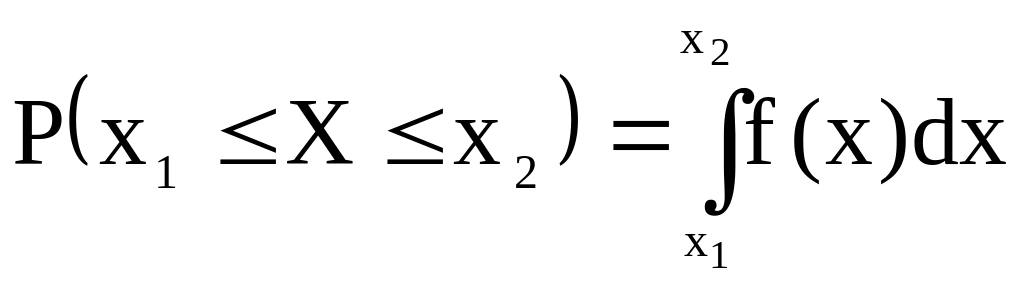Для непрерывной сл.вел. имеет смысл говорить не о вероятности точного значения, а о вероятности того, что значение сл.вел. попадёт в некоторый интервал значений. Закон распределения непрерывной сл.вел. Х задаётся функцией плотности вероятности таким образом, что . При этом и

Важнейшими непрерывными распределениями являются равномерное на некотором отрезке распределение и нормальное распределение. При равномерном на распределении при и при В этом случае вероятность попадания в некоторый интервал равна отношению длины интервала к длине отрезка

Нормальное распределение задаётся двумя параметрами: своим средним значением и разбросом вокруг него . Его плотность выражается формулой 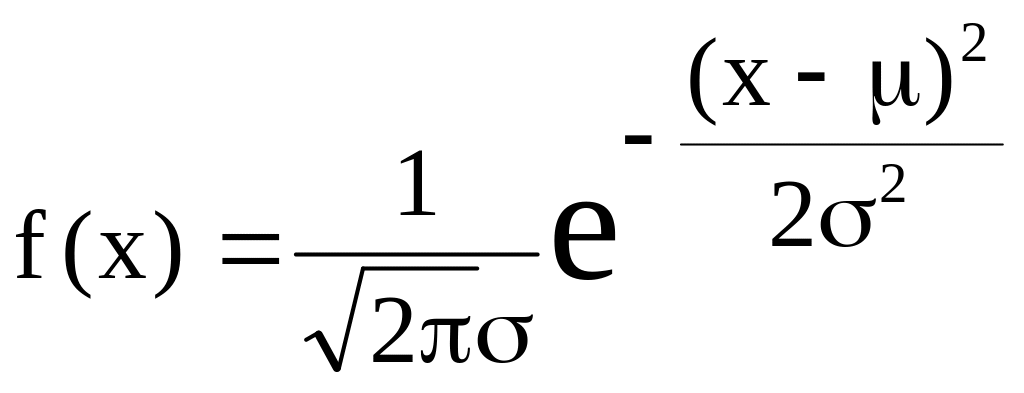. Как видно из формулы, плотность максимальна при х= и симметрично убывает в обе стороны от . Тот факт, что Х распределена по нормальному закону с параметрами ,  кратко записывают в виде Х~(,). Нормальное распределение (0,1) называется стандартным. Его плотность имеет вид .

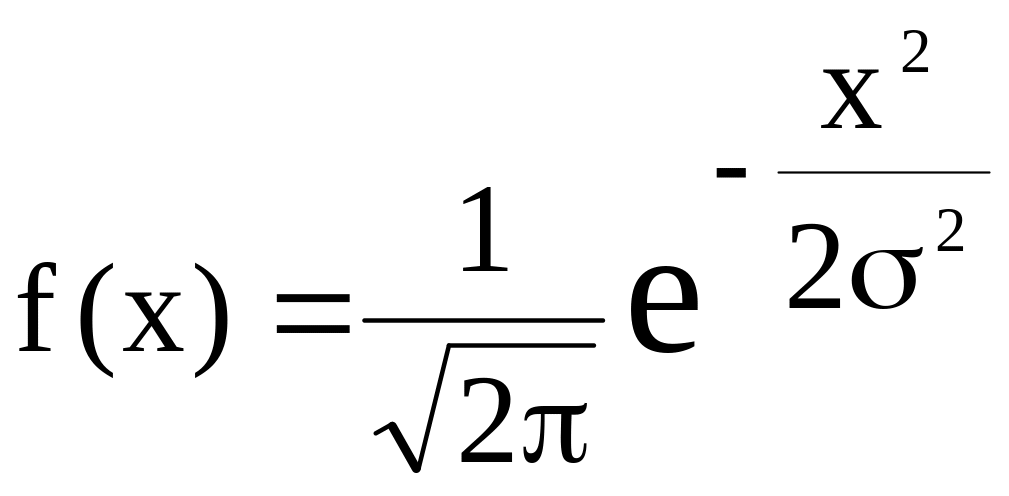Чтобы единым образом описывать дискретные и непрерывные сл.вел., для сл.вел. Х вводят функцию распределения . Для дискретной сл.вел.

Для непрерывной сл.вел.

Функция распределения- это неотрицательная функция, монотонно возрастающая от 0 до 1. Если Х- дискретная сл.вел., то - кусочнопостоянная функция со скачками в точках х₁, х₂, …, равными вероятностями этих значений. Например, для бернулиевской сл.вел.

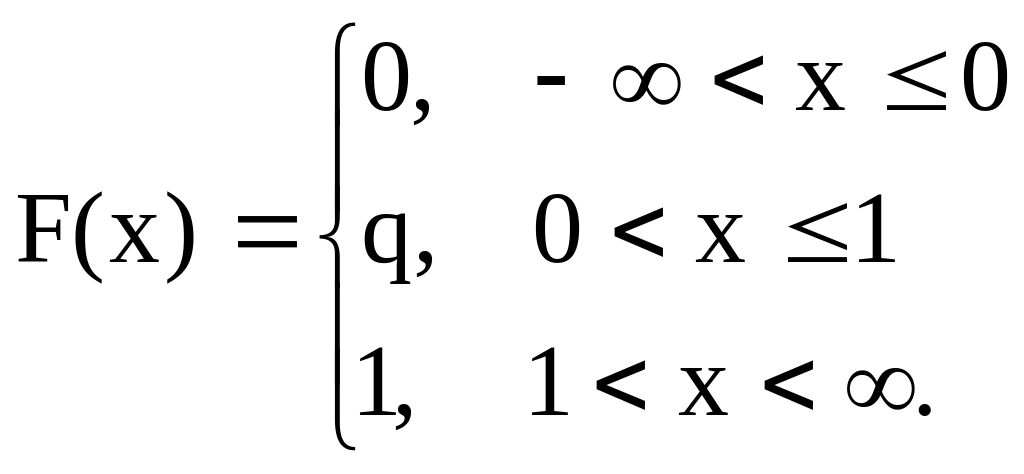
Если Х- непрерывная сл.вел., то - непрерывная функция и

Для любой сл.вел. имеет место соотношение

Для решения широкого круга вопросов, связанных со сл.вел. нет необходимости точно знать закон распределения, достаточно некоторых его числовых характеристик. Наиболее информативными и часто используемыми такими характеристиками являются математическое ожидание и дисперсия.

Математическое ожидание МХ- это средневзвешенное значение случайной величины Х. Для дискретной сл.вел. , для непрерывной сл.вел. при условии, что ряд или интеграл сходятся абсолютно.

Основные свойства математического ожидания;

1. М(сХ)=сМХ (постоянный множитель можно выносить за знак математического ожидания);

2. М(Х+У)=МХ+МУ (математическое ожидание суммы случайных величин равно сумме математических ожиданий).

Дисперсия является мерой разброса сл.вел. вокруг среднего

значения. Если МХ=, то дисперсия DX есть DX=М(X-)², при условии, что математическое ожидание существует. Используя свойства математического ожидания, легко получить эквивалентную формулу для дисперсии Дисперсия всегда неотрицательна. Корень квадратный из дисперсии называется средним квадратическим или стандартным отклонением и обозначается

Основные свойства дисперсии:

1. D(сХ)=с²DХ (при умножении сл.вел. на постоянный множитель дисперсия умножается на его квадрат);

2. если Х и У- независимые сл.вел., то D(Х+У)=DХ+DУ (дисперсия суммы независимых сл.вел. равна сумме дисперсий).

Пусть МХ=, DХ=². Тогда, как следует из приведённых

свойств, для случайной величины У= справедливо МУ=0, DУ=1. Подобное линейное преобразование часто используется и называется приведением сл.вел. к стандартному виду.

Найдём математическое ожидание и дисперсию рассмотренных ранее распределений.

1. Пусть Х- бернуллиевская сл.вел. Тогда

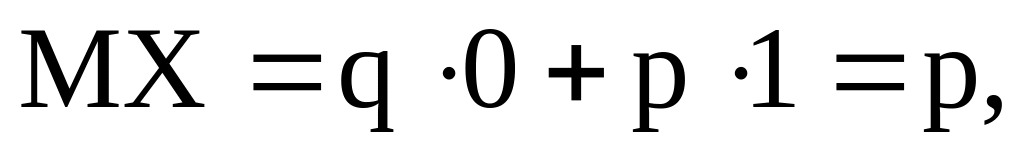
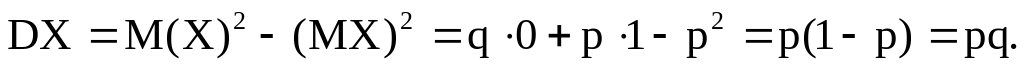
2. Пусть Х- биномиальная сл.вел. Её можно рассматривать как сумму n независимых бернуллиевских сл.вл. Поэтому

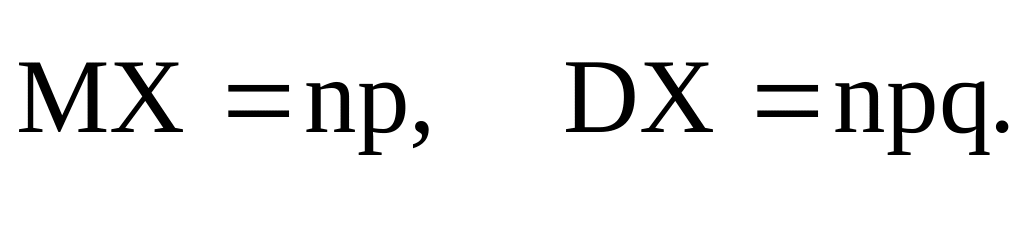
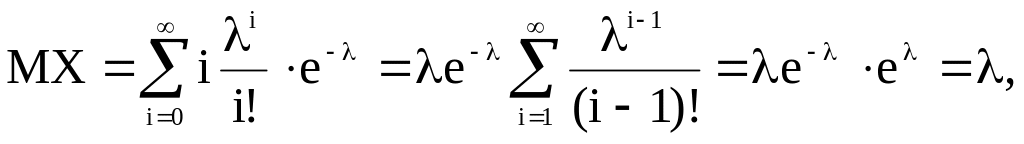
3. Пусть Х- пуассоновская сл.вел. 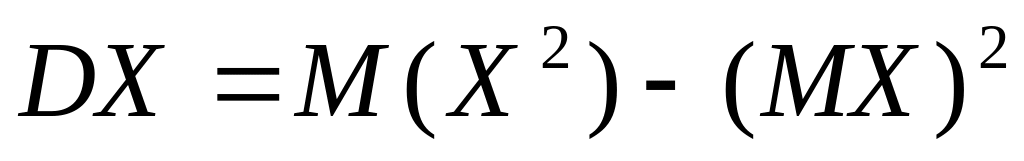= 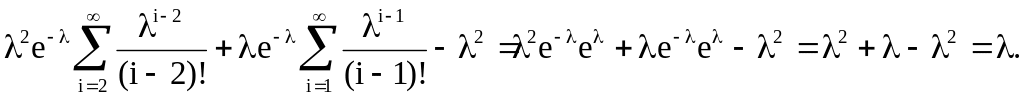Таким образом, и математическое ожидание, и дисперсия пуассоновского распределения равны .

4. Пусть Х- равномерно распределения на сл.вел. Тогда 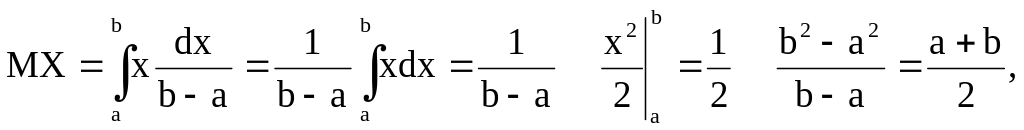т.е. математическое ожидание совпадает с серединой отрезка .

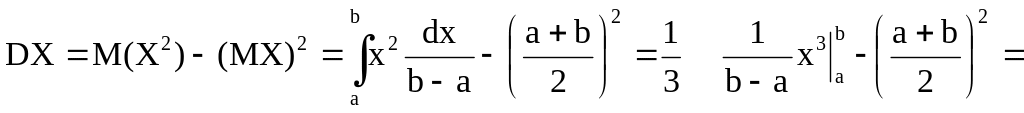
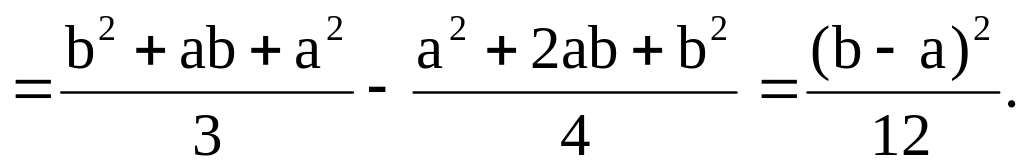
5. Если Х- нормально распределённая сл.вел. с плотностью вероятности 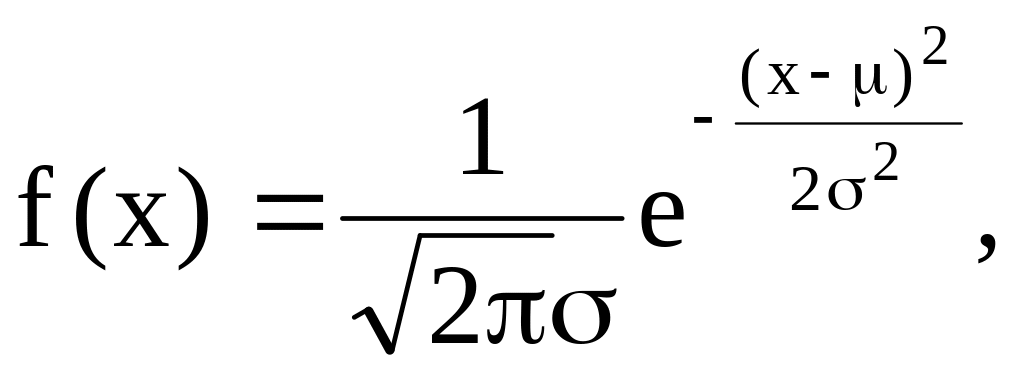то МХ=, DX=².