
Алгоритм вычислительной геометрии. / ivanovsky_4-18
.pdf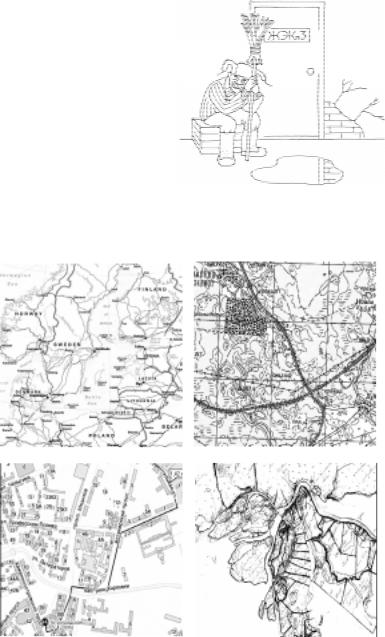
Ивановский Сергей Алексеевич, Симончик Сергей Константинович
АЛГОРИТМЫ ВЫЧИСЛИТЕЛЬНОЙ ГЕОМЕТРИИ. ПЕРЕСЕЧЕНИЕ ОТРЕЗКОВ:
МЕТОД ЗАМЕТАНИЯ ПЛОСКОСТИ
1. ВВЕДЕНИЕ |
|
|
|
|
|
Задача |
î |
пересечении |
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
прямолинейных отрезков на |
|||
|
Тема этой статьи определяет- |
|
|
плоскости кратко формули- |
||||||
|
|
|
руется так: дано конечное |
|||||||
ся не только желанием авторов |
|
|
||||||||
рассказать об одной из базовых |
|
|
множество отрезков; требу- |
|||||||
задач вычислительной гео- |
|
|
ется найти их пересечения. |
|||||||
метрии – задаче о пересе- |
|
|
Эта задача имеет разнооб- |
|||||||
чении отрезков на плоско- |
|
|
|
|
|
разные приложения. |
||||
сти, но и познакомить чи- |
|
|
 |
геоинформационных |
||||||
тателя с таким важным и |
|
|
системах (и не только в |
|||||||
эффективным приемом по- |
|
|
|
|
|
них) используются разнооб- |
||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
строения геометрических алгоритмов, как ме- |
разные географические карты. На картах |
|||||||||
тод заметания плоскости прямой линией. |
отображается множество объектов: населен- |
|||||||||
|
|
|
|
|
ные пункты, границы, реки и другие водо- |
|||||
|
|
|
|
|
|
|
емы, овраги и горы, доро- |
|||
|
|
|
|
|
|
|
ãè |
разного типа, мосты, |
||
|
|
|
|
|
|
|
линии электропередач и |
|||
|
|
|
|
|
|
|
другие |
промышленные |
||
|
|
|
|
|
|
|
объекты; на картах горо- |
|||
|
|
|
|
|
|
|
дов: улицы, скверы и пло- |
|||
|
|
|
|
|
|
|
щади, кварталы и отдель- |
|||
|
|
|
|
|
|
|
ные дома, реки и каналы |
|||
|
|
|
|
|
|
|
(см. рис. 1). Все эти объек- |
|||
|
|
|
|
|
|
|
ты представляются опреде- |
|||
|
|
|
|
|
|
|
ленными геометрическими |
|||
|
|
|
|
|
|
|
образами, многие из кото- |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
рых можно |
считать так |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
или иначе состоящими из |
|||
|
|
|
|
|
|
|
прямолинейных отрезков. |
|||
|
|
|
|
|
|
|
Поэтому определение пе- |
|||
|
|
|
|
|
|
|
ресечения географических |
|||
|
|
|
|
|
|
|
объектов, |
например, до- |
||
|
|
|
|
|
|
|
рог, рек, границ и т. п., |
|||
|
|
|
|
|
|
|
сводится |
ê |
нахождению |
|
|
|
|
|
|
|
|
пересечений |
множества |
||
|
|
|
|
|
|
|
отрезков. |
|
|
|
Рис. 1. Примеры различных карт и планов: |
|
|
В машинной графике |
|||||||
|
требуются методы удале- |
|||||||||
многие геометрические образы на них представлены |
|
|||||||||
|
ния невидимых линий и |
|||||||||
|
(или могут быть аппроксимированы) отрезками прямых линий |
|||||||||
18

поверхностей в трехмерных сценах, ког- |
|
|
||
да различные объекты сцены частично |
|
|
||
закрывают друг друга (см. рис. 2). Не имея |
|
|
||
оптимального алгоритма определения |
|
|
||
попарных пересечений отрезков из за- |
|
|
||
данного набора, из которых, как пра- |
|
|
||
вило, состоит большинство объектов |
|
|
||
сцены, трудно рассчитывать на эффек- |
|
|
||
тивную реализацию удаления невиди- |
Рис. 2. Удаление невидимых линий |
|||
мых линий. |
|
|||
|
|
|
||
В микроэлектронике возникает не- |
мы этой задачи, а также некоторые другие |
|||
обходимость проверки пересечения различ- |
||||
задачи, тесно связанные с ней. |
||||
ных компонентов интегральных схем, со- |
||||
|
|
|||
стоящих из большого количества элемен- |
Задача 1. ПРОВЕРКА ПЕРЕСЕЧЕНИЯ |
|||
тов (до миллиона и более), что невозможно |
ПРЯМОЛИНЕЙНЫХ ОТРЕЗКОВ (ПППО). |
|||
осуществить без компьютерных методов, в |
Дано: n прямолинейных отрезков на плос- |
|||
том числе без алгоритмов пересечения гео- |
кости. Требуется: определить факт пересе- |
|||
метрических объектов. |
чения хотя бы двух из них (ответ задачи – |
|||
|
|
«да», если пересекаются, или «нет» в про- |
||
2. ПЕРЕСЕЧЕНИЕ ПРЯМОЛИНЕЙНЫХ |
тивном случае). |
|||
|
|
|||
ОТРЕЗКОВ НА ПЛОСКОСТИ. |
Задача 2. ВСЕ ПЕРЕСЕЧЕНИЯ ОТРЕЗ- |
|||
ПОСТАНОВКА ЗАДАЧИ |
||||
КОВ (ВПО). Дано: n прямолинейных от- |
||||
|
|
|||
|
|
резков на плоскости. Требуется: найти все |
||
|
|
попарные пересечения отрезков. |
||
|
|
Постановку этой задачи можно уточнить, |
||
|
|
рассматривая две е¸ формы: |
||
|
|
1. Задача 2.1. ВПО-П: Задача ВПО в |
||
|
|
форме подсчета (ответ: число попарных |
||
|
|
пересечений). |
||
|
|
2. Задача 2.2. ВПО-О: Задача ВПО в |
||
|
|
форме отчета (ответ: перечень всех пар |
||
|
|
пересекающихся отрезков). |
||
|
|
Очевидно, что задача ВПО-П не слож- |
||
|
|
нее задачи ВПО-О, поскольку из ответа вто- |
||
Уточним постановку задачи о пересече- |
рой задачи можно легко (за линейное вре- |
|||
нии отрезков и рассмотрим различные фор- |
мя) получить ответ первой. |
|||
à |
Pá2 |
â |
ã |
|
|
Рис. 3. Простые (а и б) и непростые (в и г) |
многоугольники |
||
|
|
|
19 |
|

 q
q
P2
P2
P2
a) |
P1 |
á |
) |
â |
) |
P1 |
ã) |
P |
1 |
|
|
|
|
|
Рис. 4. Исходные многоугольники P1 è P2 (а и б). Случай в) P2 P1. Случай г) в точке q пересекаются ребра
Задача 3. ПРОВЕРКА ПЕРЕСЕЧЕНИЯ МНОГОУГОЛЬНИКОВ (ППМ). Дано: два простых многоугольника P1 (c n вершинами) и P2 (c m вершинами). Требуется: определить, пересекаются ли они (ответ зада- чи – «да», если пересекаются, или «нет» в противном случае).
Напомним, что простым многоугольником называется такой многоугольник, у которого никакая пара его непоследовательных ребер не имеет общих точек. Примеры простых и непростых многоугольников приведены на рис. 3.
Так как в задаче 3 входные многоугольники P1 è P2 простые, то при любом пересечении их ребер это будут ребра разных многоугольников. Пусть t (n) время, необходимое для решения задачи 1 (ПППО). Тогда факт пересечения многоугольников P1 è P2 можно определить за время t (n + m). При этом если в задаче ПППО получен ответ «да», то это означает, что многоугольники P1 è P2 пересекаются (пересекаются их границы). Если в задаче ПППО получен
q
q '
Рис. 5. Число пересечений справа от точки q равно 5, следовательно, точка q лежит внутри многоугольника. Число пересечений
справа от точки q′ равно 6, следовательно, точка q′ лежит вне многоугольника
ответ «нет», то необходимо проверить слу-
÷àè P1 Ì P2 è P2 Ì P1 (см. рис. 4). Проверку P1 Ì P2 можно выполнить,
определив для любой вершины q многоугольника P1 ее принадлежность многоугольнику P2. Если вершина q П P2, то тем же способом следует проверить P2 Ì P1. Проверка принадлежности точки q простому многоугольнику P может быть выполнена за время O(n) (см., например [1]). Идея алгоритма такова (см. рис. 5): следует под- считать число пересечений k линией y = qy сторон многоугольника, например справа от точки q = (qx, qy), тогда если k нечетно, то точка q лежит внутри многоугольника.
В статье [2] мы уже использовали понятие преобразования задач. Напомним, что задача A преобразуется в задачу B за время O(T(n)) (будем обозначать это, как
A ¾¾¾T (n) ® B ), если задачу A можно решить следующим образом:
1.Из исходных данных к задаче А сконструировать соответствующие исходные данные к задаче В за время O(T(n)).
2.Решить задачу В.
3.Из результата решения задачи В получить результат решения задачи А за время O(T(n)).
Можно подвести итог нашего обсуждения связи задачи 3 о проверке пересечения многоугольников (ППМ) и задачи 1 о проверке пересечения прямолинейных отрезков (ПППО):
ÏÏÌ ¾¾®n ÏÏÏÎ.
Отметим, что сложность алгоритмов, работающих с многоугольниками, может зависеть от того, известно ли, что многоуголь-
20

|
Рис. 6. Примеры простых многоугольников при n = 1000 |
|
|
|
||||
ник простой. Проверка простоты много- |
КОВ преобразуется в задачу 2.1 – ВСЕ ПЕ- |
|||||||
угольника не является простой задачей. |
РЕСЕЧЕНИЯ ОТРЕЗКОВ (в форме подсче- |
|||||||
Например, |
при тестировании программ, |
та), которая, в свою очередь, преобразует- |
||||||
порождающих простые n-угольники, в слу- |
ся в задачу 2.2 – ВСЕ ПЕРЕСЕЧЕНИЯ ОТ- |
|||||||
чае больших значений n визуальный ана- |
РЕЗКОВ (в форме отчета): |
|
|
|||||
лиз, как правило, неосуществим. На рис. 6 |
1 |
n |
||||||
в качестве примера приведены некоторые |
ÏÏÏÎ ¾¾® ÂÏÎ-Ï ¾¾® ÂÏÎ-Î. |
|||||||
Действительно, если иметь ответ задачи |
||||||||
простые многоугольники при n = 1000. Уже |
||||||||
здесь при данном разрешении трудно оце- |
ВПО-О в виде списка пар пересекающихся |
|||||||
нить простоту многоугольников, а во мно- |
отрезков, то прямым подсчетом можно по- |
|||||||
гих задачах, речь идет о многоугольниках |
лучить ответ задачи ВПО-П: число пересе- |
|||||||
размера около n = 1 000 000. |
чений k (k ³ 0). Далее, если k > 0, то отве- |
|||||||
Задача 4. ТЕСТ ПРОСТОТЫ МНОГО- |
том задачи ПППО является «да», если же |
|||||||
k = 0, то ответом будет «нет». |
||||||||
УГОЛЬНИКА (ТПМ). Дано: многоугольник |
||||||||
Задача ВПО-О решается очевидным ал- |
||||||||
P (c n вершинами). Требуется: определить, |
||||||||
|
|
|
n(n - 1) |
|
||||
прост ли он (ответ задачи – «äà», åñëè ìíî- |
горитмом: перебираются все |
|
ïàðû |
|||||
2 |
||||||||
гоугольник простой, или «нет» в против- |
|
|
|
|||||
отрезков и каждая пара проверяется на пе- |
||||||||
ном случае). |
|
ресечение. Этот «лобовой» алгоритм имеет |
||||||
Многоугольник прост тогда и только |
сложность O(n2 ) . Этот же алгоритм с уче- |
|||||||
тогда, когда никакая пара его ребер не пе- |
тов описанных преобразований задач 1 и 2 |
|||||||
ресекается. Следовательно, тест пересече- |
||||||||
решает и задачи ВПО-П и ПППО. Есте- |
||||||||
ния многоугольников (ТПМ) преобразуется |
||||||||
ственно задать вопрос: можно ли решить |
||||||||
в задачу проверки пересечения прямолиней- |
||||||||
все эти задачи каким-либо более эффектив- |
||||||||
ных отрезков (ПППО): |
|
|||||||
|
ным алгоритмом? Для ответа на этот воп- |
|||||||
|
|
|
||||||
|
n |
рос целесообразно сначала выявить нижнюю |
||||||
ÒÏÌ ¾¾® ÏÏÏÎ. |
||||||||
|
|
|
оценку сложности задачи ПППО, то - |
|||||
|
|
|
|
есть выяснить, каково |
необходимое |
|||
3. НИЖНЯЯ ОЦЕНКА |
|
|||||||
|
время гарантированного решения зада- |
|||||||
СЛОЖНОСТИ |
|
|
||||||
|
|
чи при произвольных входных данных. |
||||||
ПРОВЕРКИ ПЕРЕСЕЧЕНИЯ |
|
|||||||
ПРЯМОЛИНЕЙНЫХ |
|
Имеется в виду, что всегда можно |
||||||
ОТРЕЗКОВ |
|
|
предъявить для алгоритма, решающе- |
|||||
Рассмотрим задачи 1 и 2. |
го задачу, такие исходные данные, что |
|||||||
|
время работы алгоритма (или количе- |
|||||||
Используя |
преобразование |
|
||||||
ство операций алгоритма) будет не ме- |
||||||||
задач, легко показать, что за- |
||||||||
нее некоторой определенной величи- |
||||||||
дача 1 – ПРОВЕРКА ПЕРЕ- |
||||||||
|
ны, зависящей от размера входных дан- |
|||||||
СЕЧЕНИЯ |
ПРЯМО- |
|
|
|||||
|
ных задачи (в нашем случае от коли- |
|||||||
|
|
|
||||||
ЛИНЕЙНЫХ ОТРЕЗ- |
чества отрезков n). |
|
21

à) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
|
|||
á) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
0 |
|
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
|
||||||||||
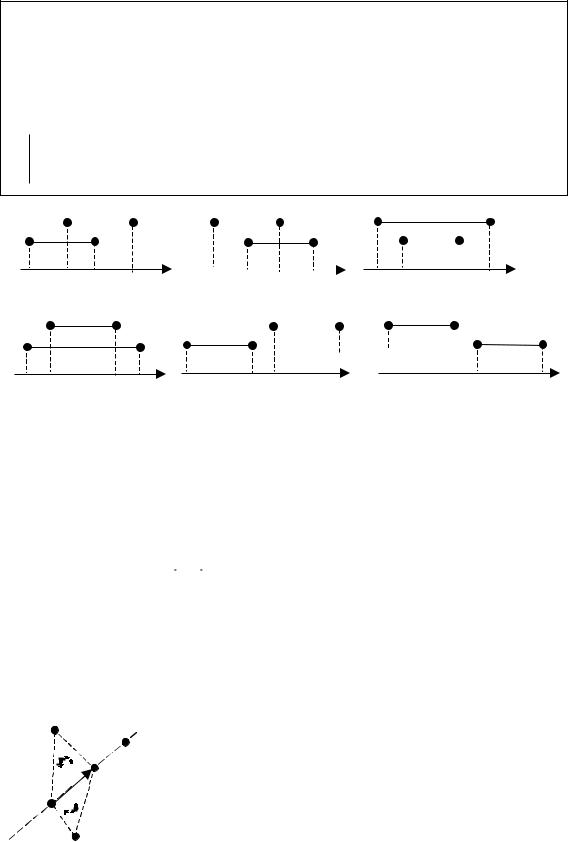
Рис. 7. Проверка наложения интервалов:
а) последовательность «01010101010101» чередующаяся – нет наложений; б) последовательность «00101100101101» не чередующаяся – есть наложения интервалов
Для выявления нижней оценки рассмотрим задачу ПППО в одномерном случае: все заданные отрезки расположены на одной прямой, и необходимо проверить, пересекаются ли хотя бы два из них. Ясно, что задача на плоскости не проще, чем задача на прямой. В одномерном случае задачу можно переформулировать так: заданы n интервалов на вещественной оси и необходимо узнать, не перекрываются ли какие-нибудь два из них. Конечно, наш «лобовой» алгоритм решает эту задачу за время O(n2). Можно поступить иначе. Пометим все левые концы интервалов знаком «0», а все правые – знаком «1» и упорядо- чим по возрастанию 2n концевых точек заданных интервалов за время O(n log n). Интервалы не перекрываются тогда и только тогда, когда после сортировки последовательность пометок является чередующейся – «0101...0101» (см. рис. 7).
Проверку чередования можно провести за время O(n) и, следовательно, решить всю задачу за время O(n log n).
Фактически этот алгоритм является преобразованием задачи ПППО в задачу сортировки и дает верхнюю оценку сложности. Для получения нижней оценки требуется преобразовать некоторую задачу с известной нижней оценкой (вычислительный прототип) в задачу ПППО. Задача сортировки на эту роль не подходит. Рассмотрим задачу ПРОВЕРКИ ЕДИНСТВЕННОСТИ ЭЛЕМЕНТОВ (ПЕЭ): даны n вещественных чисел, требуется проверить, все ли они различны. Очевидно, задача ПЕЭ преобразуется за время O(n) в задачу сортировки. Однако обратного преобразования нет. Оказывается, что нижняя оценка задачи ПЕЭ есть W(n log n) и этот факт устанавливается прямым использованием формальной вы-
числительной модели, основанной на деревьях решений (см. [1], с. 232). Покажем, что задача ПППО преобразуется в задачу ПЕЭ. Действительно, за время O(n) заданный набор из n вещественных чисел {xi} можно преобразовать в набор из n интервалов {[xi, xi]}. Эти (вырожденные) интервалы перекрываются тогда и только тогда, когда среди исходных чисел {xi} есть совпадающие. Следовательно, ПЕЭ ¾¾®n ПППО, и нижняя оценка задачи ПППО есть W(n log n), так как решив задачу ПППО за меньшее, чем W(n log n), время, мы могли бы и зада- чу ПЕЭ решить за меньшее время, что невозможно.
Итак, нижняя оценка сложности задач о пересечении отрезков на плоскости (задач ПППО, ВПО-П и ВПО-О) есть W(n log n). Достижима ли она, то есть существуют ли алгоритмы, решающие пере- численные задачи за время O(n log n)? Ответ на этот вопрос будет дан в разделе 5.
4. БАЗОВАЯ ОПЕРАЦИЯ «ПЕРЕСЕЧЕНИЕ ДВУХ ОТРЕЗКОВ»
Определяя нижнюю оценку сложности задач о пересечении отрезков, мы считали, что базовые
операции, используемые в этих задачах, выполняются за время O(1). Можно предположить, что основной
базовой операцией будет проверка пересе- чения пары отрезков.
Определять факт пересечения пары отрезков можно в два этапа. Сначала определяется факт пересечения ограничивающих прямоугольников каждого из отрезков (этот
22

à |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
á |
) |
â) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8. Ограничивающие прямоугольники: а) из пересечения отрезков следует пересечение прямоугольников; б) из пересечения прямоугольников не следует пересечение отрезков; в) из факта непересечения прямоугольников следует факт не пересечения отрезков
грубый тест выполняется быстро). Ограни- чивающий прямоугольник отрезка является наименьшим из прямоугольников, содержащих отрезок и имеющих стороны, параллельные осям координат. На рис. 8 показаны ограничивающие прямоугольники ориентированных отрезков [ pa , pb ] è [ pc , pd ] в различных ситуациях. Если ограничивающие прямоугольники не пересекаются, то и отрезки не пересекаются, если же установлен факт пересечения ограничивающих прямоугольников, то следует перейти ко второму этапу и проверить собственно пересе- чение отрезков (точный тест).
Перед проверкой пересечения прямоугольников полезно сначала определить ограничивающие прямоугольники отрезков, используя следующий вспомогательный алгоритм (листинг 1).
Два прямоугольника со сторонами, параллельными координатным осям, пересекаются тогда и только тогда, когда пересекаются и их проекции на ось x, и их проекции на ось y. Алгоритм проверки пересече- ния прямоугольников можно представить в виде алгоритма (см. листинг 2).
Условное выражение в строке 1 алгоритма иллюстрируется на рис. 9 (на примере пересечения x-проекций, то есть части конъюнкции (xb ³ xc ) and (xd ³ xa ).
Следует отметить, что в случаях, когда хотя бы один из исходных отрезков [ pa , pb ] è [ pc , pd ] вертикален или горизонтален, алгоритмы BOUNDINGRECTANGLE è RECTANGLESINTERSECT дают правильный результат.
Итак, если на первом этапе отсутствие пересечения двух отрезков не установлено тестом на пересечение ограничивающих прямоугольников, то необходимо применить точный тест. В основе теста лежит следующее утверждение: два отрезка пересекаются тогда и только тогда, когда каждый из отрезков пересекается с прямой, содержащей другой отрезок. Различные граничные случаи требуют аккуратного рассмотрения (см. далее). Отрезок [ pa , pb ] пересекается с прямой, если концы отрезка лежат по разные стороны от прямой или на прямой (хотя бы один конец). Как мы знаем [3, стр. 9], определить, лежит ли точка q = (xq , yq ) по левую или по правую сторону от прямой, содержащей ориентированный отрезок
Листинг 1. Algorithm BOUNDINGRECTANGLE ( pa , pb ) ® (p1 , p2 )
Âõîä: pa = (xa , ya ), pb = (xb , yb )
Выход: ограничивающий прямоугольник для отрезка [ pa , pb ] , заданный парой вершин (p1 , p2 ) , ãäå
p1 = (x1 , y1) – левый нижний угол прямоугольника; p2 = (x2 , y2 ) – правый верхний угол прямоугольника;
1 x1 ¬ min (xa , xb ) 2 y1 ¬ min (ya , yb ) 3 x2 ¬ max (xa , xb ) 4 y2 ¬ max (ya , yb )
5 Вернуть в качестве результата p1 = (x1 , y1) è p2 = (x2 , y2 )
23
Листинг 2. Algorithm RECTANGLESINTERSECT ( pa , pb , pc , pd ) ® Boolean
Âõîä: pa = (xa , ya ), pb = (xb , yb ), pc = (xc , yc ), pd = (xd , yd ) pa – левый нижний угол первого прямоугольника;
pb – правый верхний угол первого прямоугольника; pc – левый нижний угол второго прямоугольника; pd – правый верхний угол второго прямоугольника
Выход: True, если прямоугольники пересекаются, иначе False
1 if (xb ³ xc ) and (xd ³ xa ) and (yb ³ yc ) and (yd ³ ya )
2 then Вернуть в качестве результата True
3else Вернуть в качестве результата False
à) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
á) |
|
|
|
|
|
|
â) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xd |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
c |
|
xa |
|
|
|
xd |
|
|
|
x |
b |
|
|
|
|
xa |
xc |
|
xb |
|
x |
xc |
|
|
xb |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ã) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ä) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xa |
|
|
|
|
|
|
|
|
|
|
||
|
|
xa |
|
|
|
|
|
xb |
|
|
|
|
|
|
x |
|
|
xd xa |
|
|
x |
|
|
|
xb |
|
xc |
|
|
xd |
|
||||||||||||||||||
xc |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
c |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
³ xc ) and (xd ³ xa ), |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9. В вариантах а)–г) справедливо (xb |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
в варианте д) |
|
– |
(xb ³ xc ) and (xd |
< xa ), в варианте е) – |
(xb < xc ) and (xd |
³ xa ) |
|||||||||||||||||||||||||||||||||||||||||
[ p1 , p2 ] , или на этой прямой, можно, ана- |
На рис. 11 представлены основные ва- |
||||||||||||||||||||||||||||||||||||||||||||||||
лизируя знак ориентированной площади |
|
рианты расположения отрезков и их харак- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
S(p , p ,q) = |
1 |
|
(x |
- x )(y - y ) - (y |
- y )(x |
- x ) |
|
теристики, определяющие факт пересече- |
|||||||||||||||||||||||||||||||||||||||||
2 |
|
ния отрезков. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
q |
1 |
2 |
1 |
q |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
треугольника |
|
p1 p2q (èëè, ÷òî òî æå, âåê- |
На рис. 12 представлены некоторые из |
||||||||||||||||||||||||||||||||||||||||||||||
торного произведения [ p1 p2 , p1q] , ñì. [4] è |
|
граничных случаев (остальные легко допол- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
нить), когда хотя бы один из концов одного |
||||||||||||||||||||||||||||||||||||||||||||||||
приложение в [3]). На рис. 10 рассмотрены |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
отрезка лежит на прямой, содержащей дру- |
|||||||||||||||||||||||||||||||||||||||||||||||
различные варианты расположения точки |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
гой отрезок, и, следовательно, хотя бы одна |
||||||||||||||||||||||||||||||||||||||||||||||||
относительно отрезка. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
из ориентированных площадей равна нулю. |
|||||||||||||||||||||||||||||||||||||||
Введем вспомогательный алгоритм вы- |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Как показывают, например, варианты а) и |
||||||||||||||||||||||||||||||||||||||||||||||||
числения ориентированной площади (см. |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
б), решение о пересечении отрезков нельзя |
||||||||||||||||||||||||||||||||||||||||||||||||
листинг 3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
принять только на основе анализа ориенти- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
q′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q′′′ |
|
|
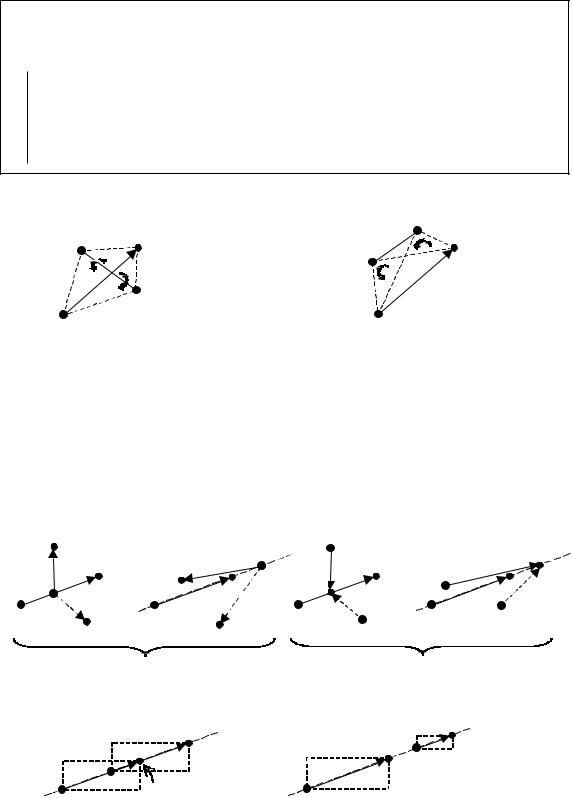
1. S(p1 , p2 ,q′) > 0 , точка q′ |
– слева от [ p1 , p2 ], |
p1 p2q′ ориен- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тирован (обходится) против часовой стрелки; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. S(p1 , p2 ,q′′) < 0 , точка q¢¢ – справа от [ p1 , p2 ], |
p1 p2q′′ îðè- |
|||||||||||||||||||||||||||
|
|
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ентирован (обходится) по часовой стрелке; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
q′′ |
|
|
|
|
|
|
|
|
|
3. S(p1 , p2 ,q′′′) = 0 , точка q¢¢¢ – на прямой, содержащей отрезок |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ p1 , p2 ], |
p1 p2q′′′ |
вырожден, точки |
p1 , p2 ,q′′′ |
– коллинеарные. |
||||||||||||||||||||||||
Рис. 10. Различные варианты расположения точки q относительно отрезка [ p1 , p2 ]
24
Листинг 3. Algorithm AREA (pa , pb , pc) ® 2S(pa , pb , pc )
Âõîä: pa = (xa , ya ), pb = (xb , yb ), pc = (xc , yc )
Выход: удвоенная ориентированная площадь треугольника pa pb pc
1Вернуть в качестве результата (xa - xb )(yc - ya ) - (yb - ya )(xc - xa )
{если результат > 0, то точка pc лежит слева от ориентированного отрезка [ pa , pb ] ,
если результат < 0, то точка pc лежит справа от ориентированного отрезка [ pa , pb ] , если результат = 0, то точка pc лежит на прямой, содержащей отрезок [ pa , pb ] , то есть точки pa , pb , pc коллинеарные}
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
á |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
S ( pa , pb , pd ) > 0 |
|
|
S ( pa , pb , pc ) > 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
S ( pa , pb , pc ) > 0 |
|
|
|
p d |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
pc |
|
|
|
|
|
|
|
|
|
|
|
|
|
pb |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pb |
pc |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pa |
|
|
|
|
|
|
|
|
|
|
|
|
|
pa |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
S ( pa , pb , pd ) < 0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Рис. 11. Анализ пересечения отрезков [ pa , pb ] è [ pc , pd ]: |
|||||||||||||||
|
|
|
|
|
а) отрезки пересекаются, и S( pa , pb , pc ) |
è S( pa , pb , pd ) |
|
имеют разные знаки; |
||||||||||||||||||
|
|
|
б) отрезки не пересекаются, и S( pa , pb , pc ) |
è S( pa , pb , pd ) |
имеют одинаковые знаки |
|||||||||||||||||||||
рованных площадей. Отметим, что в нашем подходе вариант г) не может появиться на втором этапе, так как ограничивающие прямоугольники здесь не пересекаются.
Итак, граничные случаи требуют дополнительного анализа, который может быть проведен с использованием следующего алгоритма (см. листинг 4).
à) |
|
|
|
|
á) |
|
|
pb |
pb |
|
pa |
pa |
pb |
|
|
|
|
pd |
pd |
|
|
|
pd |
|
|
pa |
|
|
pa |
|
pd |
|
pb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pa |
pc |
pb |
pc |
pb |
pc |
pa |
pc |
|
S ( pc , pd , pa ) = 0, |
|
|
S ( pc , pd , pb ) = 0, |
||||||||||
|
S ( pc , pd , pb ) ¹ 0 |
|
|
S ( pc , pd , pa ) ¹ 0 |
||||||||||
â) |
|
|
|
|
|
|
pb |
ã) |
|
pa |
|
|
|
|
|
pa |
|
|
|
|
|
|
|
|
|
|
|
pb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
pd |
|
|
|
pd |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pc |
|
|
||
pc |
|
|
|
|
|
|
|
|
= 0, |
|||||
|
S ( pc , pd , pa ) = 0, |
|
|
S ( pc , pd , pa ) |
||||||||||
|
S ( p |
c |
, p |
d |
, p ) = 0 |
|
|
S ( pc , pd , pb ) = 0 |
||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|||
Рис. 12. Граничные случаи, когда ориентированная площадь равна ну лю
25

Листинг 4. Algorithm BETWEEN (pa , pb , pc ) → Boolean
Âõîä: pa = (xa , ya ), pb = (xb , yb ), pc = (xc , yc )
Предусловие: точка pc лежит на прямой, содержащей отрезок [ pa , pb ]
Выход: True, если точка pc является точкой ориентированного отрезка [ pa , pb ] , иначе False
1 if min (xa , xb ) ≤ xc ≤ max (xa , xb ) and min (ya , yb ) ≤ yc ≤ max (xa , xb )
2 then Вернуть в качестве результата True
3else Вернуть в качестве результата False
Подытожим наши соображения в алгоритме SEGMENTSINTERSECT (листинг 5).
В тех случаях, когда кроме факта пересечения пары отрезков требуется определить точку их пересечения, алгоритм SEGMENTSINTERSECT следует дополнить. Рассмотрим основные необходимые для этого соотношения, оставляя читателю модификацию алгоритма SegmentsIntersect в ка- честве упражнения.
Для представления отрезков [ pa , pb ] è [ pc , pd ], заданных концевыми точками, удобно использовать параметрические уравнения [4]. Например, все точки отрезка [ pa , pb ] описываются следующим уравне-
íèåì:
pab (t) = pa + (pb − pa )t,
где вещественный параметр t [0,1]. Оче- видно, pab (0) = pa è pab (1) = pb , à âíóò-
|
Листинг 5. Algorithm SEGMENTSINTERSECT ( pa , pb , pc , pd ) → Boolean |
|
Âõîä: pa = (xa , ya ), pb = (xb , yb ) – концы ориентированного отрезка [ pa , pb ] , |
|
pc = (xc , yc ), pb = (xb , yb ) – концы ориентированного отрезка [ pc , pd ], |
|
Выход: True, если отрезки пересекаются, иначе False |
1 |
(p1 , p2 ) ← BoundingRectangle ( pa , pb ) |
2 |
(p3 , p4 ) ← BoundingRectangle ( pc , pd ) |
3 |
if not RectanglesIntersect ( p1 , p2 , p3 , p4 ) |
4then Вернуть в качестве результата False
{ограничивающие прямоугольники не пересекаются}
5else {ограничивающие прямоугольники пересекаются}
6 |
s1 |
← Area (pc , pd , pa ) |
7 |
s2 |
← Area (pc , pd , pb ) |
8 |
s3 |
← Area (pa , pb , pc ) |
9 |
s4 |
← Area (pa , pb , pd ) |
10 |
if |
((s1 > 0 and s2 < 0) or (s1 < 0 and s2 > 0)) and |
|
|
((s3 > 0 and s4 < 0) or (s3 < 0 and s4 > 0)) |
11then Вернуть в качестве результата True
12else if (s1 = 0) and Between (pc , pd , pa )
13then Вернуть в качестве результата True
14else if (s2 = 0) and Between (pc , pd , pb )
15then Вернуть в качестве результата True
16else if (s3 = 0) and Between ( pa , pb , pc )
17then Вернуть в качестве результата True
18else if (s4 = 0) and Between ( pa , pb , pd )
19then Вернуть в качестве результата True
20else Вернуть в качестве результата False
26

ренним точкам pab (t) отрезка [ pa , pb ] ñî- |
|
ных или горизонтальных отрезков, система |
||||||||||||||||||||
ответствуют значения параметра |
[ pa , pb ] . |
|
уравнений для определения t и s, а, следо- |
|||||||||||||||||||
Аналогичное уравнение запишем для отрез- |
|
вательно, и формулы вычисления значений |
||||||||||||||||||||
êà [ pc , pd ]: |
|
|
|
|
|
|
|
|
t или s могут быть при необходимости уп- |
|||||||||||||
pcd (t) = pc + (pd - pc )s, |
|
|
|
рощены. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где параметр s О [0,1]. |
|
|
|
|
|
|
|
|
|
5. АЛГОРИТМ НАХОЖДЕНИЯ |
|
|||||||||||
Поскольку алгоритм SEGMENTSINTERSECT |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
ПЕРЕСЕЧЕНИЯ ОТРЕЗКОВ |
|
|||||||||||||||||
при определении факта пересечения пары |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
отрезков разбирает все необходимые ситу- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ации, то будем интересоваться точкой пе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ресечения отрезков только тогда, когда ус- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
тановлено, что отрезки пересекаются и при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
этом не лежат на одной прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для вычисления точки пересечения за- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
пишем уравнение |
pab (t) = pcd (s) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
pa + ( pb - pa )t = pc + (pd - pc )s, |
|
|
|
|
Более эффективным, чем «лобовой» ал- |
|||||||||||||||||
которое определяет значения параметров t |
|
|
|
|
||||||||||||||||||
|
горитм, имеющий сложность O(n2), являет- |
|||||||||||||||||||||
и s, соответствующие точке пересечения q. |
|
ся алгоритм, основанный на применении ме- |
||||||||||||||||||||
Покоординатная запись этого уравнения |
|
|||||||||||||||||||||
|
тода заметания плоскости. Метод подска- |
|||||||||||||||||||||
xa + (xb - xa )t = xc + (xd - xc )s, |
|
|||||||||||||||||||||
зан геометрической природой задач. В на- |
||||||||||||||||||||||
xa + (xb - xa )t = xc |
+ (xd - xc )s, |
|
шем случае речь идет о плоском замета- |
|||||||||||||||||||
является системой двух линейных уравне- |
|
нии, поскольку рассматриваются задачи на |
||||||||||||||||||||
плоскости. |
|
|
|
|
|
|
||||||||||||||||
ний для определения неизвестных t и s. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Опишем идею метода плоского замета- |
||||||||||||||||||
Нетрудно убедиться, что решением этой |
|
|
|
|
||||||||||||||||||
|
ния применительно к задаче нахождения |
|||||||||||||||||||||
системы будут |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
всех пересечений отрезков, а затем перей- |
||||||||||||||||
t = [(xa - xc )(yd -yc) + (xd - xc )(yc - ya )] / D, |
||||||||||||||||||||||
|
дем к описанию алгоритма. Возьмем вер- |
|||||||||||||||||||||
s = [(xb - xa )(yc -ya) + (xa - xc )(yb - ya )] / D, |
|
тикальную прямую L, которая разбивает |
||||||||||||||||||||
где D есть определитель системы |
|
|
|
|
плоскость на левую и правую полуплоскос- |
|||||||||||||||||
D = (xa - xb )(yd -yc ) + (xd - xc )(yb - ya ). |
|
ти (см. рис. 13). Пусть каждая из этих по- |
||||||||||||||||||||
луплоскостей содержит концы заданных от- |
||||||||||||||||||||||
В нашем случае D ¹ 0, поскольку мы |
||||||||||||||||||||||
|
резков. Решение нашей задачи может быть |
|||||||||||||||||||||
заранее знаем, что отрезки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пересекаются (то есть |
íå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
параллельны) и заведомо не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
лежат на одной прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставив вычисленное |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|||||||
значение t или s в уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|||||
pab (t) = pa |
+ (pb |
- pa )t |
èëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
pcd (t) = pc |
+ (pd |
- pc )s ñî- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ответственно, получим точку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пересечения, например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
q = pa + (pb - pa )t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разумеется, в вырожденных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
случаях, рассмотренных в ал- |
|
|
x1 |
|
x2 |
|
|
x3 |
|
x4 |
|
xpp |
|
x5 |
|
xq x6 |
x7 x8 x9 |
x10 |
||||
горитме SEGMENTSINTERSECT, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
||||||
а также в случае вертикаль- |
|
Рис. 13. Заметание плоскости вертикальной прямой L |
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
27
