МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

______

Санкт-Петербургский Государственный

Электротехнический университет «ЛЭТИ»

_____________________________________________________________________

КАФЕДРА МОЭВМ

ОТЧЕТ

по лабораторной работе

по дисциплине

КОМБИНАТОРНЫЕ АЛГОРИТМЫ

Метод дерева регионов в задаче регионального поиска

Выполнили: Долгих П.

Матвеенцев Ю.

Герус А.

Группа: 8308

Преподаватель: Ивановский С.А.

Санкт-Петербург

2003

Постановка задачи

Рассматривается задача регионального поиска. Задан файл – множество точек в d-мерном евклидовом пространстве. Образцом для поиска является гиперпрямоугольная область (т.е. декартово произведение интервалов на различных координатных осях). Требуется определить, какие точки попадают в область.

Предполагается, что заданы сразу все точки, а потом поступает множество запросов.

Идея алгоритма

В постановке задачи наиболее важно то, что задаются сразу все точки, а уже затем поступают массовые запросы. Если бы запрос был один или точки часто удалялись и добавлялись в файл, то задача свелась бы к простому перебору всех точек. Но в нашем случае можно произвести предобработку файла. В результате этой предобработки будет построена специальная структура данных – дерево регионов. Обработка запросов будет производиться уже с использованием дерева регионов.

Как будет показано ниже, рассматриваемый алгоритм имеет следующие оценки сложности (N – количество точек файла, d – размерность пространства):

1. время предобработки – O(N log ^d-1 N)

2. память, необходимая для хранения дерева регионов – O(N log ^d-1 N)

3. время обработки одного запроса - O(log ^d N)

Вспомогательные структуры данных Дерево отрезков

Дерево отрезков - это структура данных, созданная для работы с такими интервалами на числовой оси, концы которых принадлежат фиксированному множеству из N абсцисс.

Дерево отрезков – это двоичное дерево T(l,r), которое для заданных целых чисел l и r, таких, что l<r, состоит из корня v с параметрами B[v] = l, E[v] = r, а если r-l < 1, то имеет также левое поддерево и правое поддерево .

На рис. 1 показано дерево отрезков для l = 1, r = 12.

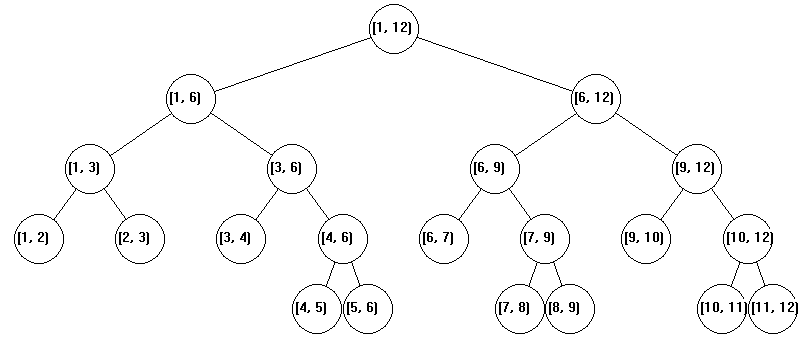
Рисунок 1 – Дерево отрезков для l=1, r=12

Интервалы, принадлежащие множеству {[B[v], E[v]]: v – узел дерева T(l,r)}, называются стандартными интервалами дерева T(l, r).

В дерево отрезков T(l, r) может быть вставлен отрезок, концы которого принадлежат множеству {l, l+1, …, r}. При r-l>3 отрезок [b, e] может быть разбит в набор из не более чем стандартных интервалов дерева T(l, r). Разбиение производится за время O(log N). Соответствующие узлы дерева отрезков называются узлами отнесения.

Обозначения:

ЛСЫН[v] – корень левого поддерева дерева с корнем v

ПСЫН[v] - корень правого поддерева дерева с корнем v

procedure ВСТАВИТЬ(b, e; v)

begin

if (bB[v]) and (E[v]e) then назначить [b, e] узлу v

else

begin

if (b < ) then ВСТАВИТЬ(b, e; ЛСЫН[v]);

if ( < e) then ВСТАВИТЬ(b,e; ПСЫН[v]);

end

end

Вставка отрезка [b, e] в дерево отрезков T производится путем обращения ВСТАВИТЬ(b, e; корень(T)).

Например, отрезок [2, 9] можно разбить на следующие стандартные интервалы: [2, 3], [3, 6] и [6, 9].

Дерево регионов для d = 2

Это дерево отрезков T(1, N+1) (N – количество точек в файле), в котором в каждом узле v находится упорядоченная последовательность тех точек файла, нормализованные абсциссы которых лежат в интервале [B[v], E[v]). Нормализация абсциссы означает следующее: точки нумеруются от 1 до N в порядке возрастания абсцисс, а затем абсцисса каждой точки заменяется на номер этой точки.

На рис. 2 показаны точки файла, а на рис.3 построенное для этого файла дерево регионов. Точки на рис. 2 не пронумерованы в порядке возрастанию абсцисс. Нумерация здесь нужна, чтобы показать, какие точки соответствуют каждому узлу дерева.

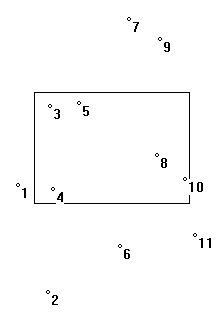
Рисунок 2 - Расположение точек файла на плоскости

Рисунок 3 - Построенное дерево регионов

Алгоритм регионального поиска при d=2

Входные данные:

1. файл

2. построенное для этого файла дерево регионов T

3. образец для поиска – прямоугольник с координатами левого нижнего угла (x0, y0) и правого верхнего (x1, y1).

Алгоритм:

1. b := (количество точек файла, абсциссы которых меньше x0)+1

e := (количество точек файла, абсциссы которых не больше x1)+1

2. Обратиться к процедуре ВСТАВИТЬ(b, e, корень(T)). При этом будет получено множество узлов отнесения.

3. Из каждого узла отнесения выбрать те точки, ординаты которых, попадают в отрезок [y0, y1]. Для этого находиться точка z1 с наименьшей ординатой, попадающая в диапазон [y0, y1], с помощью бинарного поиска. Затем бинарным поиском находиться точка z2 с наибольшей ординатой, попадающая в диапазон [y0, y1]. Наконец, выбираются все точки между z1 и z2, включая их самих.

Результатом обработки запроса будут все выбранные таким способом точки.

Пример работы алгоритма:

На рисунке 2 показано расположение точек файла на плоскости и образец для поиска, на рисунке 3 показано дерево регионов. Узлы отнесения и выбранные точки подчеркнуты.

Обобщение на случай d>2 и оценка сложности

Обобщение на d измерений можно провести весьма естественно. Пусть в d-мерном пространстве с координатными осями x₁, x₂,…,x_d задано множество S из N точек. Эти координаты будут обрабатываться в следующем порядке: сначала х₁, затем x₂ и т. д. Предположим также, что все значения координат нормализованы. Дерево 'регионов строится рекурсивно следующим образом:

(1) Первичное дерево отрезков Т* соответствует множеству {x₁(p): pS}. Для каждого узла v из Т* обозначим через S_d(v) – множество точек из S, проецирующихся на отрезок [B[v], E[v]) по координате х₁. Определим (d – 1)-мерное множество:

S_d-1(v) {(x₂(p), …, x_d(p)): pS_d(v)}

(2) Узел v из Т* имеет указатель на дерево регионов для S_d-1(v).

Переходя теперь к анализу сложности метода, заметим, во-первых, что при d  2 каждый узел отнесения из проекции запросного региона на ось х₁ (их всего O(logN)) порождает отдельную (d–1)-мерную задачу регионального поиска. В частности, узел v порождает поиск на n(v) E [v] – В [v] точках. Обозначая через O(N, d) время поиска для файла из N штук d-мерных точек, получаем простое рекуррентное соотношение:

Первый член в правой части этого уравнения появился из-за поиска на первичном дереве отрезков, а второй член объясняется наличием (d – 1)-мерных подзадач. Поскольку существует не более 2log₂N – 2 узлов отнесения и n(v)  N (очевидно), то получаем

Q(N, d) = О(logN)Q(N, d–1).

Поскольку Q(N, 1) = O(logN) для двоичного поиска, то получаем оценку времени поиска:

Q(N,d) = O((logN)^d).

Обозначая через S(N, d) память, занятую деревом регионов, получаем рекуррентное соотношение

где первый член в правой части соответствует памяти, занятой первичным деревом, а второй член соответствует всем (d – 1)-мерным деревьям. Оценка второго члена очень проста, если N есть степень 2; в противном случае будет использована столь же эффективная простая аппроксимация. Существует не более двух узлов v с , не более четырех – с и т. д. Поэтому эту сумму можно оценить сверху следующим

образом:

Учитывая эту аппроксимацию и замечая, что S(N, 1)= О(N) — память под прошитое двоичное дерево, получаем решение

S (N, d) = О (N log^d-1 N).

Для оценки времени предварительной обработки можно следовать той же самой схеме рассуждений.

В частности, при d = 2 эти меры — время запроса, память и время предварительной обработки — выглядят так: O(log² N+k), O(NlogN) и O(NlogN)) соответственно.