Линейная дискриминантная функция Фишера
•Данный подход не требует предположений о нормальном распределении данных.
•Пусть имеется обучающая выборка: x1, x2, ... xN , где:
N1 элементов из множества X1
N2 элементов из множества X2
•Общее число элементов N = N1 + N2
•Задача состоит в построении разделяющей функции для двух классов:
X1 = {xi} i=1..N1 X2 = { x j} j=1..N2
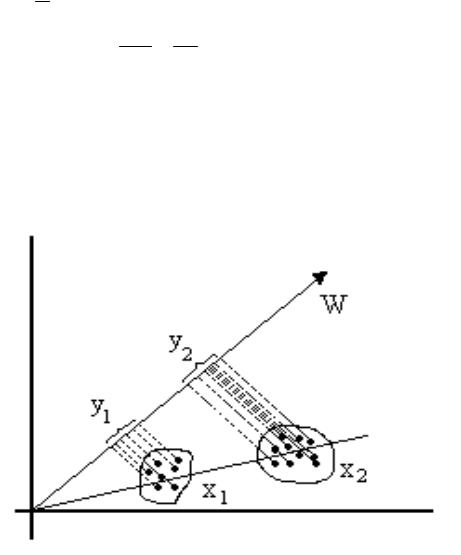
•Задача Фишера состоит в построении вырожденного линейного преобразования:
y = WT x, ║W║ = 1 y = ║W║║x ║cos( W , X)
фактически это выражение дает нам проекции векторов X на вектор W
•У Фишера такое преобразование рассматривается как проекция на ось W: { x} {y} = Y
•Нужно найти такой вектор W, чтобы множества Y1 и Y2 были наиболее разнесены (то есть, удалены друг от друга).
•Критерий разнесения может быть выбран разным.
•Исходить будем из следующих параметров: для каждой выборки определим среднее значение:
mi = |
|
1 |
|
|
xi |
|
|
|
|
|
||||
|
|
Ni |
|
χi |
|
|
|
|
|
|
|
|||
mi |
|
χ |
|
|
|
|
|
|
|
|||||
1 |
|
|
|
1 |
|
1 |
|
|||||||
~ = |
Ni y Yi |
yi = |
|
WTxi = WT{ |
Ni χ χi |
x} = WT mi |
||||||||
Ni x χi |
||||||||||||||
|
|
|
|
|||||||||||
• Далее мы строим | m~1 - m~ 2 |:
| ~ |
- ~ | = WT( |
|
|
|
) - это скалярная величина |
m1 |
m2 |
m1 - m2 |
|||
•Далее проблема состоит в оценке функции разброса:
~ |
2 |
= |
~ |
|
2 |
|
Si |
|
) |
- разброс внутри класса |
|||
|
(y - mi |
|
||||
|
|
y Yi |
|
|
|
|
~ |
|
~ 2 |
~ 2 |
|
|
|
S |
2 = S1 |
+ S2 |
|
|
- суммарный разброс |
|
•Разброс внутри класса – это нечто вроде дисперсии, только ненормированной.
1 ~2 - средняя дисперсия выборки в Y.
N S
•Далее идет дело техники: как это вычислить и как оптимизировать.
•Мы определяем матрицу разброса внутри класса:
S |
= |
(W |
x - W |
mi) |
= |
W |
(x - mi) W (x - mi) = |
~ 2 |
|
T |
T |
2 |
|
T |
T |
i |
x χi |
|
|
|
|
x χi |
|
|
|
|
|
|
|
||
|
= WT |
(x - mi)(x - mi)T W = WT [ (x - mi)(x - mi)T]W = |
|||||
|
x χi |
|
|
|
|
|
x χi |
=WT Si W
Si – матрица разброса внутри Xi.
•Таким образом получаем следующий результат:
~ 2
Si = WT Si W
S1 + S2 = SW - суммарная матрица разброса для всех результатов.
S~ 2 |
+ S~ 2= WT SW W |
1 |
2 |
~~
•Таким же образом можно представить ( m1- m2)2:
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (WT m1- WT m2)2 |
= WT( m1 |
- m2)WT( m1 - m2) = |
|||||||||||||||
( m1 |
- m2 )2 |
||||||||||||||||
=WT( m1 - m2)( m1 - m2 )T W = WT SB W
•Матрица SB - матрица разброса между классами
•Тогда мы получаем искомый критерий в следующем виде:
J( W) = WTSB W WTSW W
• Далее стоит задача оптимизации данного отношения (мы должны его максимизировать).
• Рассмотрим свойства матрицы SB:
SB = ( m1 - m2)( m1 - m2)T
1.это квадратная матрица размерности n n
2.произведение этой матрицы на произвольный вектор
SB |
|
= ( |
|
1 - |
|
2)( |
|
1 - |
|
2 )T |
|
= С( |
|
1 - |
|
2) |
|
m |
m |
m |
m |
m |
m |
||||||||||
a |
a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C - скаляр |
дает вектор, который по направлению совпадает с разностью
( m1 - m2 )
3. ранг матрицы SB равен единице, это легко показать, если представить ее в виде ddT:
d1d1 d1d2 |
... d1dn |
|
|
|
|
|
|
|
|
|
|
||||||||||
d2d1 |
d2d2 |
... d2dn |
|
|
|
|
|
|
|
|
. |
|
|
|
= ( |
dd1 dd2 ddn) . |
|||||
. |
|
|
|
|
|
|
|
|
|
|
dnd1 |
dnd2 |
... dndn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- матрица вырожденная и ранг ее равен единице.
Условная оптимизация по Лагранжу
•Запишем функцию Лагранжа: F = WT SB W - WT SW W,
где -произвольная константа Эта функция зависит от W
Мы должны найти производную этой функции по вектору :
dWdF = 2 SB W - 2 SW W = 0
d(XT AX) |
= 2A |
|
- такое правило существует, его легко |
||
X |
|||||
|
|
|
|
|
|
dX |
|
|
|
доказать |
|
|
|
|
|
|
|
• Получаем следующее: SB W - SW W
• C( m1 - m2 ) = SW W , отсюда окончательно имеем:
|
= SW-1 ( |
|
1 |
- |
|
2 ) C . |
|
W |
|||||||
m |
m |
||||||
|
|
|
|
|
|
|
•Так как вектор W произвольной длины, положим C =1, тогда имеем :
W= SW-1 ( m1 - m2).
•Соответственно линейный дискриминант Фишера получается в следующем виде:
y = |
|
|
T |
|
|
= XTW = |
|
|
SW-1( |
|
|
|
) - это проекция вектора |
|
на |
|
|
|
|
|
|
|
|
||||||||
W |
|
|
|
|
|||||||||||
X |
X |
|
|||||||||||||
|
|
|
|
m1 - m2 |
X |
||||||||||
ось W |
|
|
|
|
|
|
|
|
|
|
|
|
|
||