Классификация на основе оценки апостериорной вероятности
•Как было показано ранее, решение о выборе класса может быть принято на основе оценки апостериорной вероятности, рассчитанной по теореме Байеса, и выбора наибольшей вероятности
f ( i | X ) |
qi f ( X | i ) |
, i 1...m |
m |
||
|
qi f ( X | i ) |
|
|
i 1 |
|
•Априорная вероятность известна из закона многомерного нормального распределения
f ( X | i ) |
1 |
exp( |
1 |
( X Mi )T 1 ( X Mi )) Aexp((*)) |
|
(2 )n / 2 | | 1 |
2 |
||||
|
|
|
Классификация на основе оценки апостериорной вероятности
• Раскроем показатель (*)
(*) 12 X T 1 X 12 MiT 1 X 12 MiT 1Mi 12 MiT 1 X
• Учитывая, что
MiT 1 X X T 1Mi
•В результате мы получим следующее выражение
|
|
1 |
X |
T |
|
1 |
|
exp (x) |
f ( X | i ) exp |
2 |
|
|
X |
||||
|
|
|
|
|
|
|
|
|
где (x) X T 1M i |
|
1 M iT |
1M i |
|||||
|
|
|
|
|
2 |
|
|
|
Классификация на основе оценки апостериорной вероятности
•Соответственно, учитывая, что первый сомножитель не зависит от номера класса, так как рассматривается случай равных матриц ковариации, получаем формулу
f( i | X ) mqie i
qie i
i 1
• Решение о классе объекта ищется на основе критерия максимума
max i (x) или |
imax arg max i |
i |
|
Классификация двух нормальных распределений с неравными матрицами ковариации
• Рассмотрим построение статистической решающей |
|
функции при условии «∑1 отлично от ∑2» и заданных |
|
математических ожиданиях классов M1 |
и M2 |
• Построим отношение правдоподобия |
Λ(X) = |
f(X | 1) / f(X | 2) , где |
|
f (X | i ) |
|
1 |
exp( 1 |
(X Mi )T |
1 (X Mi )) |
|
|
|
||||||||||||||
(2 )n/ 2 | | 1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
• Рассмотрим отношение правдоподобия |
|
|
|
|
|
|
|
|
|
|||||||||||||
(X ) |
|
|
|
2 |
|
12 |
exp |
1 (X M |
)T 1 (X M |
) 1 |
(X M |
|
) 1 |
(X M |
|
) |
K |
|||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
2 |
1 |
1 |
1 |
2 |
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
K C(1| 2)q2 |
|
известное |
|
отношение |
|
|
|
|
|
|
|
|||||||||||
C(2 |1)q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Классификация двух нормальных распределений с неравными матрицами распределения
• Логарифмируем отношение правдоподобия
ln |
|
|
2 |
|
12 |
12 X M2 T 21 (X M2 ) (X M1 )T 1 1 (X M1 ) ln( K) |
|
|
|
|
|||||
|
|
|
|||||
|
|
1 |
|
12 |
|||
|
|
||||||
|
|
|
|
|
|
|
|
• После приведения к общему виду получим следующую запись
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
(X ) 12 X T 2 |
11 X |
X T ( 1 |
1M1 |
21M2 ) |
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(M |
1M |
|
M |
|
1M |
|
) ln |
|
|
|
|
|
|
|
ln K |
||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
1 |
1 |
|
1 |
|
|
2 |
2 |
|
2 |
|
|
|
|
1 |
|
12 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Классификация двух нормальных распределений с неравными матрицами ковариации
• Если выполняется случай Σ1 = Σ2 = Σ, получаем выражение, изученное ранее
X T 1 (M1 M2 ) 12 (M1T 1 1M1 M2T 21M2 ) ln K
•В этом случае мы имеем линейную дискриминацию
•При неравных матрицах ковариации дискриминация будет нелинейной и разделяющая поверхность будет определяться уравнением U(X) = 0
•На следующем рисунке показаны разделяющие поверхности
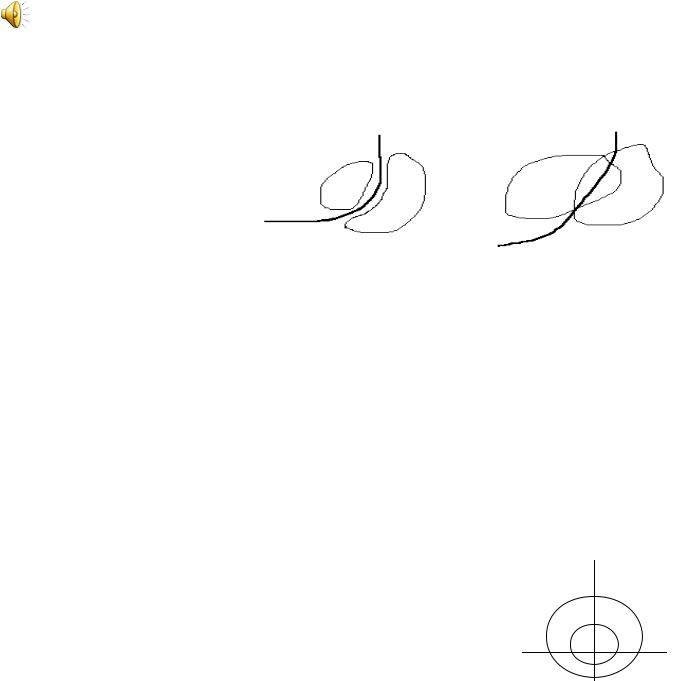
Классификация двух нормальных распределений с неравными матрицами ковариации
•Рассмотрим случай, когда математические ожидания обоих распределений равны нулю : M1 = M2 = 0. Матрицы ковариации в этом случае определяются следующим образом
|
|
2 |
0 |
|
|
|
2 |
0 |
|
|
|
1 |
|
|
|
2 |
|
||
|
|
2 |
|
|
|
2 |
|
||
1 |
|
0 |
|
2 |
0 |
||||
|
|
1 |
|
|
|
2 |
|
||
• А линии равной плотности представлены на следующем рисунке
Классификация двух нормальных распределений с неравными матрицами ковариации
•В самом частном случае K = 1 q1 = q2 из чего следует ln K = 0 C(2|1) = C(1|2)
U ( X ) 1 X T ( 1 |
1 ) X ln |
|
|
2 |
|
|
|
12 |
0 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
1 |
|
12 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
M |
|
M |
|
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||
|
|
|
|
2 |
|
0 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Классификация двух нормальных распределений с неравными матрицами ковариаций
|
|
|
1 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
||
|
|
22 |
12 |
|
|
|
|
|
2 |
|||||
1 |
1 |
|
|
|
|
|
|
|
ln |
2ln |
||||
2 |
1 |
|
|
|
|
|
1 |
|
1 |
|
12 |
|
||
|
|
|
|
|
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
1 |
||||
|
|
|
|
|
2 |
2 |
|
|
|
|||||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
• Теперь подставим все заготовки в общую формулу
|
|
1 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
X1 |
|
|
|
|
||||
22 |
12 |
|
|
|
|
|
2 |
|
|||||||
U ( X ) 2 |
|
|
|
|
1 |
|
1 |
|
|
|
2 ln |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
X1 , X2 |
|
|
|
|
X |
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
2 |
2 |
|
|
|
|||||||
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
1 |
2 2 |
2 ( X12 |
X22 ) |
2 ln |
|
||
2 |
1 |
|||||||||
|
|
1 2 |
|
|
|
|||||
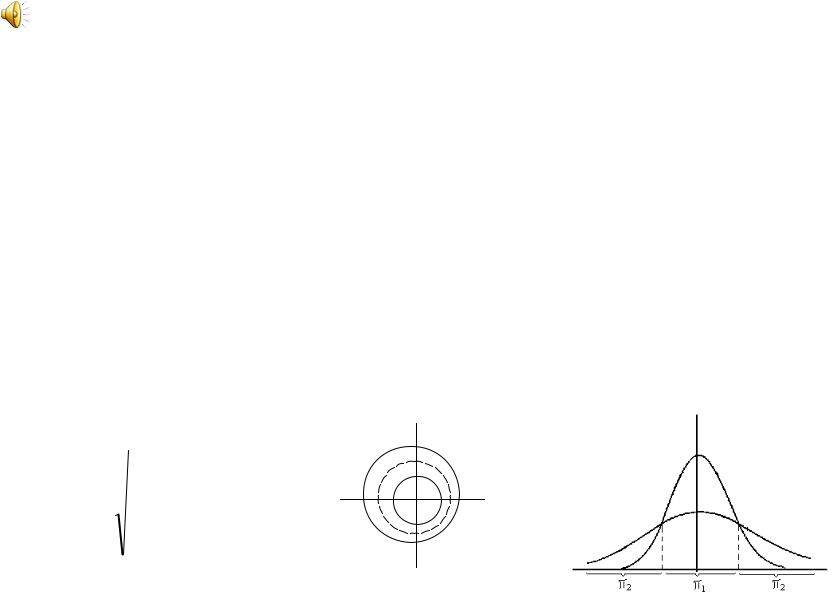
Классификация двух нормальных распределений с неравными матрицами ковариации
• Решаем уравнение U(x) = 0 и получаем уравнение сферы
|
4ln |
2 |
|
|
||
X12 X22 |
|
|
|
|
|
R2 так обозначим радиус полученной сферы |
|
|
|
1 |
|
||
|
1 |
|
1 |
|
||
|
|
|
||||
|
22 |
12 |
|
|
||
|
|
|
|
|||
• Таким образом, разделяющая поверхность выглядит очень просто
|
|
|
ln |
2 |
|
|
||
R 2 |
|
1 |
|
|
||||
|
1 |
|
|
1 |
|
|
||
|
|
|
|
|
||||
|
|
12 |
|
|
|
|||
|
|
22 |
|
|
||||
На рисунке справа показан случай в одномерной области