6.6. Классификация наблюдений в случае нескольких генеральных совокупностей

рассмотрим проблему классификации наблюдений в слу­чае нескольких генеральных совокупностей. Для этого мы распространим методы предшествующего параграфа на случай более чем двух генеральных совокупностей. Пусть —т генеральных совокупностей с плотностями распределения вероятностей р₁ (х),..., р_т (х) соответ­ственно. Мы хотим разбить пространство наблюдений на т попарно непересекающихся областей R₁ .. ., R_m. Если наблюдение попадает в область R_i, то мы скажем, что оно произведено над . Пусть цена ошибочной классификации наблюдения, произведенного над, как наблюдения над равна С (j|i). Вероятность этой ошибочной классификации равна

P(j|i, R)= . (I)

Предположим, что нам известны априорные вероятности q₁ .... q_m того, что выборка произведена из соответствую­щей генеральной совокупности. Тогда математическоеожидание потерь будет равно

(2)

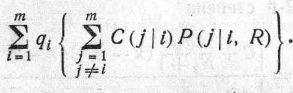
Области R_m мы желаем выбрать так, чтобы сде­лать (2) минимальным.

Так как нам известны априорные вероятности, соответ­ствующие каждой генеральной совокупности, то можно опре­делить условную вероятность того, что наблюдение произве­дено над определенной генеральной совокупностью, при условии, что компоненты вектора x имеют данные значения. Условная вероятность того, что наблюдение произведено над генеральной совокупностью , равна

' . (3)

Если мы охарактеризуем наблюдение как наблюдение над , то математическое ожидание потерь будет равно

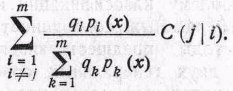(4)

Мы получим минимум математического ожидания потерь, если выберем j так, чтобы (4) было минимальным. Рассмотрим сумму

для всех j (5)

и выберем j так, чтобы (5) было минимальным. (Если мини­мум (5) достигается при двух различных значениях j, то можно выбрать любое из них.) Этот метод относит точку x к одной из областей . Повторяя его для каждой точки x, мы определим наши области R₁ .... R_m. Следовательно, метод классификации заключается в том, что наблюдение классифицируется как наблюдение над , если его резуль­таты попадают в.

Теорема 6.6.1. Если априорная вероятность того, что наблюдение произведено над генеральной совокуп­ностью с плотностью распределения вероятностей (x) (i=1, . . ., m), равна q_r и цена ошибочной класси­фикации этого наблюдения как наблюдения над , рав­на С (j|i), то области классификации , ..., R_m, при которых математическое ожидание цены является ми­нимальным, определяются следующим образом: об­ласть R_k состоит из тех точек х, для которых

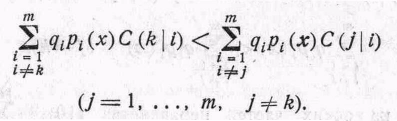(6)

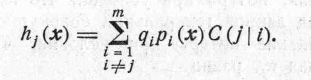
[Если (6) выполняется для всех индексов j (j k), за исключением h некоторых индексов, для которых нера­венство заменяется равенством, то такая точка может быть отнесена к любой из h+1генеральных совокуп­ностей, соответствующих этим индексам.] Если вероят­ность равенства между правой и левой частями (6) равна нулю для любых k и j при условии, что наблю­дение произведено над (i — любое), то метод, дающий минимум потерь, является единственным с точностью до множеств нулевой вероятности. Докажем это утверждение. Пусть

(7)

Тогда математическое ожидание потерь для метода R будет равно

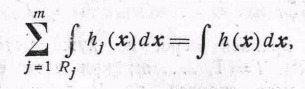(8):

где для х из h(x) = (x). Для метода Бейеса, описан­ного в теореме, h (х) есть (х) =h_i(x)-. Поэтому раз­ность математических ожиданий потерь для метода R* и любого другого метода R равна

(9)

;

Равенство может выполняться лишь в том случае, когда h= min h_i (х) для всех х из R_j за исключением мно­жеств нулевой вероятности.

Посмотрим, как можно применить этот метод в случае, когда С(j|i)=1 для всех i и j (i j). Тогда в R_k

(10)

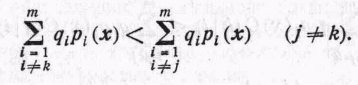
Вычитая из обеих частей неравенства (10)

получим

(11)

В этом случае точка х принадлежит R_k,, если k есть индекс, для которого q_ip_i (х) максимальна, т. е. — наиболее вероятная генеральная совокупность.

Предположим теперь, что априорные вероятности нам неизвестны. Тогда мы не можем определить безусловное математическое ожидание потерь, соответствующих данному методу классификации. Однако можно определить математи­ческое ожидание потерь при условии, что наблюдение про­изводилось над данной генеральной совокупностью. Матема­тическое ожидание потерь при условии, что наблюдение произведено над , равно

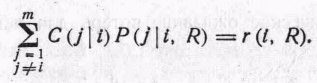(12)

Метод R, по крайней мере, не хуже метода R*, если r (i, R) (i, R*), i = 1,… m; при этом если хотя бы одно из неравенств строгое, то R лучше R*. Метод R является допустимым, если не существует метода R*. кото­рый был бы лучше R. Класс методов является полным, если для любого метода R, не принадлежащего этому классу,существует метод R*, входящий в этот класс, который лучше R.

Покажем, что метод Бейеса является допустимым. Пусть R — метод Бейеса, а R* — некоторый другой метод. Поскольку метод R является методом Бейеса,

(13)

Предположим, что r(i, )r(i, R), i = 2, .... т и >0. Тогда

, (14)

и r(1, R)r(1, R*). Аналогично, если q_i > 0, то r(i,R)r(i, R*). Таким образом, R* не может быть лучше R и, следовательно, R — допустимый метод.

Теорема 6.6.2. Если, q_i > 0 (i = 1, ..., m), то метод Бейеса является допустимым.

Теперь предположим, что C(i|j)=1, ij, и P{} = 0. Из последнего условия следует, что все p_i(х) положительны на одних и тех же множествах (за исключением множеств меры 0). Пусть q_i = 0 для i =1, ...,t и q_i > 0 для i= t+1, ...,m. Тогда для решения Бейеса множество R_i (i=1, ..., t) пусто (с точ­ностью до множества нулевой вероятности), как это видно из (11), т. е. для х из R_i p_m(x) =0 . Отсюда следует, что для

i=1,....,t r(i,R)==1-P(i|,R) = 1.

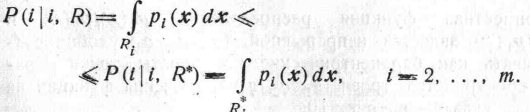
Поэтому (R_t+1, .... R_m)—решение Бейеса для задачи, содержащей p_t+1(x), .... р_т(х) и q_t+1, ..., q_m. Из тео­ремы 6.6.2 следует, что никакой метод R*, для которого Р(i|i, R*) > 0 (i = 1, ....t), не может быть лучше метода Бейеса. Теперь рассмотрим метод R* такой, что содержит множество положительной вероятности, так чтоР(1| 1, R*)>0. Для метода R*, лучшего, чем R,

(15)

В таком случае метод R**, где пусто, i=1, ..., t,

, i = t+l, .... т— 1, и =, дал бы риск такой, чтоР(i|i, R**) = 0, i=l, ...,t, P(i|i, R**) = P(i| i,R*)P(i|i, R), i= t+1, ....m-1.

P(m|m, R**)>P(m|m,R*)P(m|m, R). (16)

Т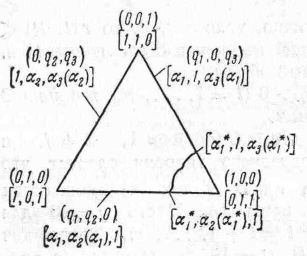огда метод () был бы лучше, чем (R_t+1, ..., R_m) для (m-t-мерного решения, что противоречит предшествую­щим рассуждениям.

Теорема 6.6.3. Если C(i|j)=1 при l j и Р = 0, то метод Бейеса является допу­стимым.

Теперь покажем, что до­пустимые методы являются методами Бейеса. Мы огра­ничимся лишь случаем m=3. Предположим, что

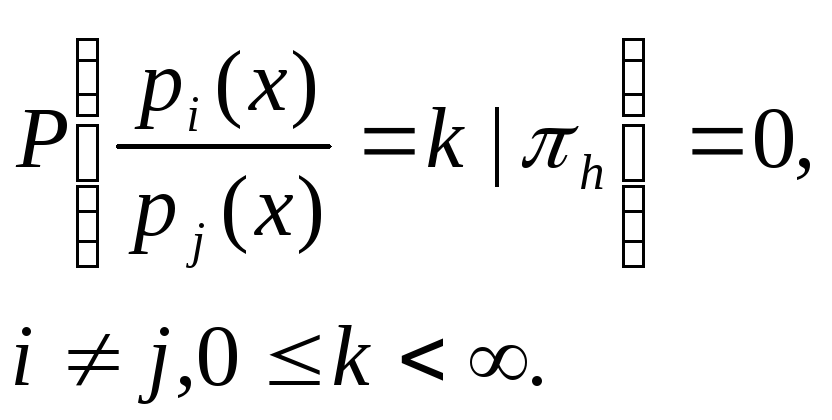(17)

Это означает, что функция распределения p_i(x)/(x) для любого и совместнаяфункция распределения двух отношений являются непрерыв­ными (см. задачу 45 главы 2).

Пусть (R)=1—P(i|i,R) — вероятность принять не­правильное решение в случае, когда выборка производится из и используется метод R. Если R является методом Бейеса, то (R) есть функция q₁ q₂, q₃, скажем . Это непрерывная функция переменных q₁, q₂,, q₃;например,

(18)

и совместная функция распределения p₂(x)/p₁(x) и р_э(х)/р₁(x) является непрерывной. (q₁, q₂, q₃) удобно рас­сматривать как барицентрические координаты точки. Гра­ницы пространства троек (q₁ q₂, q₃) и значения функций на границах указаны на рис. 10.

Пусть теперь R* — допустимый метод и (R*) = . По­кажем, чтоR* — метод Бейеса. Рассмотрим совокупность методов Бейеса, для которых (q₁ ,q₂,,q₃)= Еслиq₃=0, то фактически мы имеем дело с двумерным реше­нием, и поэтому что есть наименьшееприусловии (получается из результатов для двумерного случая). Поэтому и =1. Аналогично, если q₂=0, то и=1. Геометрическое место точек (,q₂,, q₃), для которых есть непрерывная кривая¹), соединяющая точки инепрерывно изменяется отдо 1, то существует точка, для которой. Поэтому существует метод Бейеса такой, что и () =. Поскольку метод является допустимым (по теореме 6.6.3), (). но так как методR* — допусти­мый, ()=. Вследствие единственности решения Бейеса

R* = .

Теорема 6.6.4. Если (17) верно, то любой допу­стимый метод является методом Бейеса.

Доказательство приведенной выше теоремы показывает, что класс методов Бейеса является полным. Для любого заданного метода R* существует метод Бейеса , который по крайней мере не хуже R* (это следует из полноты класса методов Бейеса). Но если не хуже R*, а R* не хуже , то эти методы совпадают (с точностью до множества нуле­вой вероятности нуль).

Далее, класс методов Бейеса является минимальным пол­ным классом, поскольку он совпадает с классом допусти­мых методов.

Теорема 6.6.5. Если (17) верно, то класс методов Бейеса является минимальным полным классом.

Можно рассмотреть также минимаксное решение. Суще­ствует решение Бейееа, для которого , ибо сово­купность точек, для которых, является связной и включает точки, для которых=1, и точки, для которых= 0. Вследствие непрерывности существует точка, для которой. Так как этот метод является допусти­мым, то не существует никакого другого метода, имеющего меньший максимум вероятности ошибки (т. е. метода, для которого каждый риск будет меньше). Поэтому получается минимаксный метод.

Для ознакомления с общей теорией статистических ре­шений отсылаем читателя к работам Вальда [3] и Блекуэлла и Гиршика[1]. Другим методом решение мини­максной проблемы было получено Мизесом [1].