Ответы на экзаменационные вопросы по АиГ / 11

11.

Рациональные корни многочленов с целыми коэффициентами.

Число с называется корнем многочлена Р(х), если Р(с)=0

Теорема

Многочлен степени n имеет не более n корней.

Пусть многочлен степени n имеет k корней, причем k>n.

Тогда, если х₁ – корень многочлена, по теореме Безу получим P(x)=(x-x₁)G(x), где G(x) – многочлен степени n-1, он имеет k-1 корней.

Продолжая процесс деления на х-х_i придем к многочлену I степени, который имеет больше одного корня, чего не может быть.

Применим

Теорема 1

Если все коэффициенты многочлена степени n, где n>0, - целые числа, и корень с этого многочлена тоже целое число, то с – делитель свободного члена.

Пусть дан многочлен , тогда при делении на х-с мы получим частное и остаток r. поскольку все a_i и r – целые числа, то b_i тоже целые.

По схеме Горнена: r=cb_n-1 +a_n=0, так как Р(х) делится на Q(x) нацело. Тогда a_n=-cb_n-1, а это и значит, что корень многочлена – делитель его свободного члена.▲

Теорема 2.

Если многочлен с целыми коэффициентами и со старшим коэффициентом равным 1 (приведенный многочлен) имеет рациональный корень, то этот корень – целое число.

Дан многочлен .

Предположим противное. Пусть - его корень, причем дробь несократима.

Подставим значение корня:

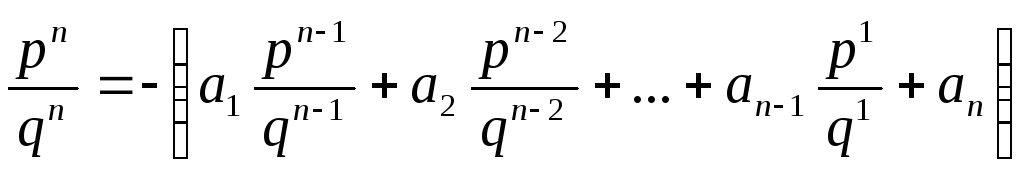Умножим обе части на q^n-1

, в правой части равенства – целое число, а значит и в левой части должно быть целое число, что противоречит нашему утверждению. Значит, корень – целое число.▲