9

III. Л.В.П. Rn 1

§9. Линейное векторное пространство Rn: вектор,линейная комбинация векторов; скалярное произведение векторов, норма вектора и их свойства. 1

§10. Линейная зависимость векторов; базис ЛВП Cn(Rn). 3

§11. Базис ЛВП Cn(Rn): разложение вектора по базису; ортогональный базис. 4

§12. ЛВП R3: вектор и направленный отрезок; свойства скалярного произведения векторов в R3. 6

§13. Векторное произведение в R3 и его свойства. 9

III. Л.В.П. Rⁿ

§9. Линейное векторное пространство Rⁿ: вектор,линейная комбинация векторов; скалярное произведение векторов, норма вектора и их свойства.

1)Рассмотрим множество матриц-столбцов размерности (nx1)

EMBED Equation.3 , элементы которого назовем "n"- мерными числовыми векторами, а числа x_i- координатами вектора.

2)Определим над векторами операции равенства, сложения и умножения на скаляр (число) как соответствующие операции над матрицами-столбцами (поэлементно).

Определение 1. Линейным векторным пространством Rⁿ (читается "эр-эн") называется множество "n"-мерных числовых векторов, в котором определены операции равенства, сложения и умножения на скаляр.

Следствие. В ЛВП Rⁿ выполняются "аксиомы 1-8 линейного пространства":

(1) ! нулевой элемент - нулевой вектор EMBED Equation.3

(2) ! противоположный элемент - противоположный вектор EMBED Equation.3

EMBED Equation.3

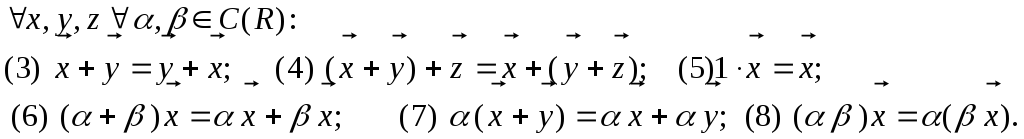
Определение 2. Если EMBED Equation.3 , вектор EMBED Equation.3 называется линейной комбинацией векторов EMBED Equation.3 с коэффициентами с_i.

Определение 3. Скалярным произведением (с.п.)векторов EMBED Equation.3 называется число, равное сумме произведений соответствующих координат множителей: EMBED Equation.3

Например, EMBED Equation.3

Свойства скалярного произведения векторов. (Доказать самостоятельно).

1)(x,y)=(y,x)=x^ty=y^tx ; 2)(cx,y)=c(x,y); 3)(cx+dy)z=c(x,z)+d(y,z)

4)(x,x)=x_i²0

Определение 4. Два вектора EMBED Equation.3 называются ортогональными, если их с.п. равно нулю EMBED Equation.3

Определение 5. Множество векторов {a_i;i=1..m} называется ортогональным, если составляющие его векторы попарно ортогональны: ij:(a_i,a_j)=0. Например, {i=[1;0;0]^t; j=[0;1;0]^t; k=[0;0;1]^t} - ортогональная система трехмерных векторов.

Определение 6. Нормой вектора "порожденной скалярным произведением", называется неотрицательное число, равное арифметическому значению квадратного корня из суммы квадратов его координат:

EMBED Equation.3

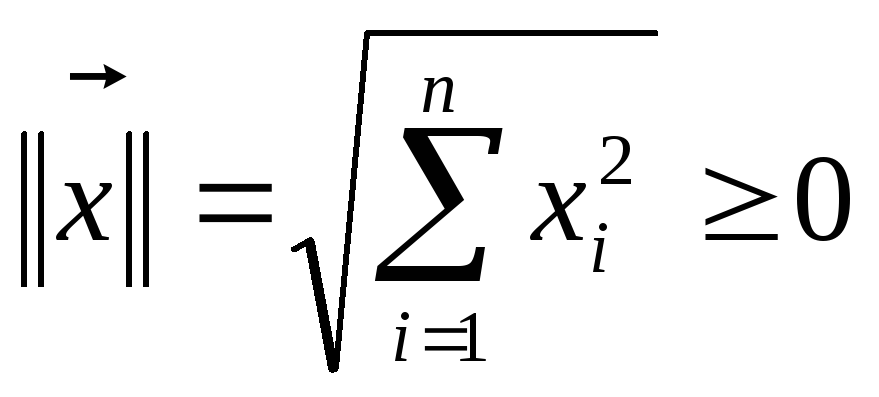
Например, ||1,-2;3||=14; ||0||=0

Свойства нормы вектора:

1)||x||=0x=0; 2) ||x||²=(x,x); 3) ||x||=||x||; 4) ||x+y||||x||+||y|| - "правило треугольника".

§10. Линейная зависимость векторов; базис ЛВП Cⁿ(Rⁿ).

Пусть задан набор векторов EMBED Equation.3

Рассмотрим уравнение с неизвестными коэффициентами c_i; i=1:n

EMBED Equation.3 , (1)

которое равносильно однородной СЛАУ, столбцами матрицы которой являются векторы набора.

Очевидно, что это уравнение всегда имеет "тривиальное" - нулевое решение - c_i=0; i=1:m. Существуют ли ненулевые решения, т.е. может ли линейная комбинация векторов быть равной нулевому вектору, если хотя бы один из коэффициентов не равен нулю ?

Определение. Набор (совокупность) векторов EMBED Equation.3 называется линейно независимым, если уравнение (1) имеет единственное -нулевое решение. В противном случае набор (совокупность) векторов называется линейно зависимым.

Следствия.

1. Если набор векторов является линейно зависимым, хотя бы один из них является линейной комбинацией других.

Док-во. Пусть уравнение (1) имеет ненулевое решение, например с₁#0. Тогда

EMBED Equation.3 EMBED Equation.3

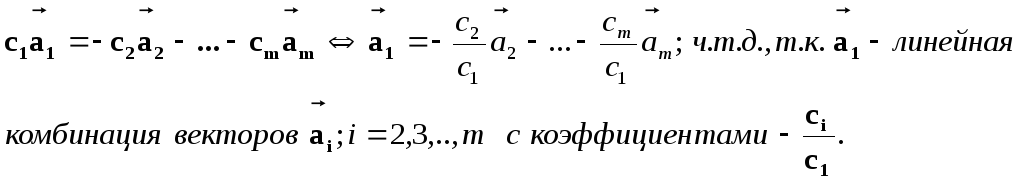
2. Если набор векторов содержит нулевой вектор, он является линейно зависимым.

3. Если количество векторов в наборе больше их размерности (m>n), набор является линейно зависимым.

Док-во. Однородная СЛАУ не бывает несовместной. При m>n она имеет кроме нулевого множество ненулевых решений.

Задача. "Исследовать линейную зависимость заданного набора векторов."

EMBED Equation.3

§11. Базис ЛВП Cⁿ(Rⁿ): разложение вектора по базису; ортогональный базис.

EMBED Equation.3 Определение. Набор EMBED Equation.3 "n" линейно независимых "n" -мерных векторов называется базисом ЛВП Сⁿ(Rⁿ).

Следствия.

1)Из т. Крамера и определения базиса ЛВП

EMBED Equation.3

следует, что набор векторов EMBED Equation.3 является базисом ЛВП тогда и только тогда, когда определитель квадратной матрицы, составленной из векторов набора, не равен нулю: EMBED Equation.3 2) Существует бесконечно много базисов ЛВП Rⁿ - базис Rⁿ образуют столбцы любой невырожденной матрицы порядка "n" . Например, столбцы единичной матрицы образуют "стандартный базис" EMBED Equation.3 .

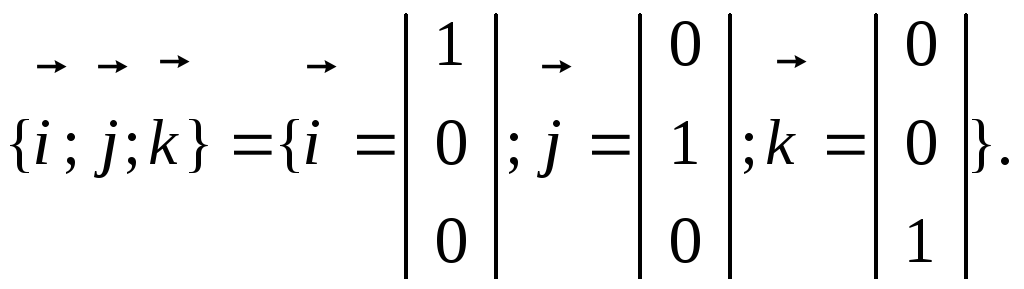Пусть EMBED Equation.3 -базис ЛВП и EMBED Equation.3

Определение. Равенство EMBED Equation.3 называется разложением вектора по базису.

Теорема. Любой вектор ЛВП единственным образом представляется в виде линейной комбинации базисных векторов x=b₁a₁+b₂a₂+…+b_na_n.

EMBED Equation.3

Док-во.

Пусть {a₁,a₂,..,a_n}- базис Rⁿ _<=> detA=det[a₁,a₂,..,a_n]≠0. Запись (*) равносильна МУ Ab=x, которое по т. Крамера имеет единственное решение - вектор коэффициентов b=[b₁,b₂,..,b_n]^t разложения (*).

Примеры.

EMBED Equation.3

Определение. Базис EMBED Equation.3 называется ортогональным, если образующие его векторы попарно ортогональны EMBED Equation.3

Теорема. "Коэффициенты c_i разложения вектора x по ортогональному базису равны EMBED Equation.3

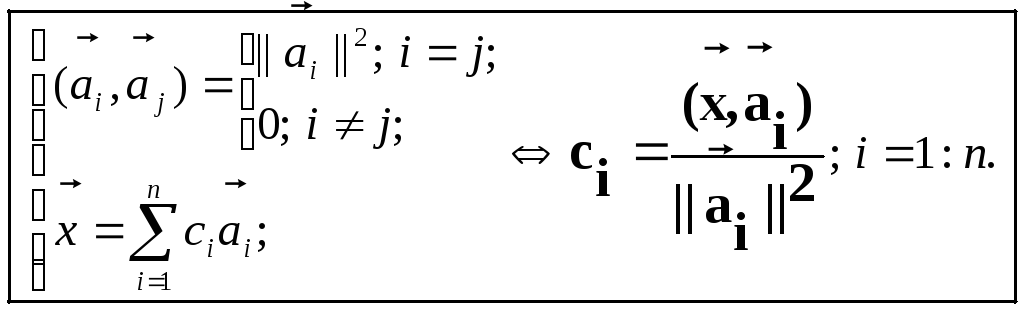
Док-во. Домножим равенство EMBED Equation.3

§12. ЛВП R³: вектор и направленный отрезок; свойства скалярного произведения векторов в R³.

ЛВП R³ -множество трехмерных числовых векторов с вещественными координатами, в котором определены (I) равенство, (2) сумма, (3) произведение на вещественное число и (4) нулевой элемент-нулевой вектор так, что для суммы векторов и произведения вектора на число выполняются 8 аксиом линейного пространства.

Другим примером ЛВП является ЛВП направленных отрезков, для которого соответствующие определения (1),(2),(3),(4), данные в средней школе, также удовлетворяют аксиомам 1-8.

Аксиомы ЛВП направленных отрезков.

1. н. отрезки параллельны, сонаправлены и имеют равную длину.

2. АВ+AC=AD; AB-AC=CA - правило параллелограмма.

X

3. λAB ||AB (направленные отрезки колинеарны  солинейны  лежат на параллельных прямых) и | λAB |=|λ|| AB |; |λ| -«коэффициент растяжения», причем <=>

4. AB=0- «нулевой» направленный отрезок <=> |AB|=0.

Установим взаимно-однозначное соответствие между этими ЛВП.

Введем в трехмерном пространстве прямоугольную систему координат OXYZ и сопоставим каждой точке A(x_a,y_a,z_a) направленный отрезок ОА, алгебраические проекции которого на координатные оси равны (x_a,y_a,z_a), и радиус-вектор r_A=[x_a,y_a,z_a]^t. Аналогично поступим с точками В и С : B(x_b,y_b,z_b) ОB  r_B=[x_b,y_b,z_b]^tR³; C(x_c,y_c,z_c)ОC  r_C=[x_C,y_C,z_C]^tR³.

Из определения суммы направленных отрезков и векторов получим

ОA+OB=OC(x_C=x_b+x_a;y_b+y_a;z_b+z_a)  r_B+r_A= r_C=[x_b+x_a;y_b+y_a;z_b+z_a]^t;

Аналогично : AB=OB-OA(x_b-x_a;y_b-y_a;z_b-z_a);; r_B-r_A=[x_b-x_a;y_b-y_a;z_b-z_a]^t.

В дальнейшем будем отождествлять направленный отрезок и соответствующий трехмерный вектор Например, будем писать : 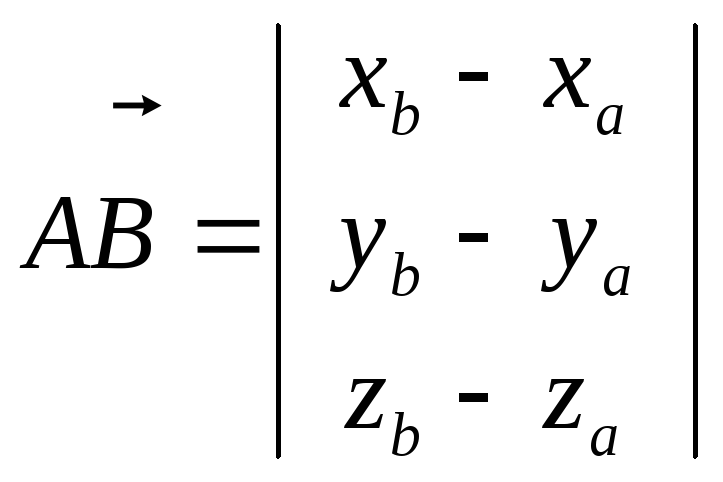- вектор R³  отрезок «из т.А в т. В».

Из принятого отождествления двух ЛВП следует «ну очень полезная» геометрическая интерпретация (иллюстрация) трехмерных векторов:

1)«норма вектора» ||a|| = |a| длина направленного отрезка»;

2) Условие колинеарности векторов - направленных отрезков a и b:;

a b ab a=b

3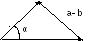) Рассмотрим треугольник, образованный векторами  направленными отрезками a, b, a-b. Из теоремы «косинусов» для направленных отрезков:

a если -угол между н.отрезками, то

|a-b|²=|a|²+|b|²-2|a||b|cos(α) квадрат длины н.о. !!!

Из свойств же скалярного произведения векторов:

||a-b||²=(a-b,a-b)=(a,a)+(b,b)-(a,b)-(b,a)= =||a||²+||b||²-2(a, b).

квадрат нормы вектора !!!

Сравнивая два результата, получаем «геометрические» свойства СП в R³:

- С.П. равно произведению длин соответствующих н. Отрезков на косинус угла между ними;

(2) Алгебраическая проекция одного н.отрезка на другой

равна отношению С.П. соответствующих векторов к норме вектора.

a c

b

(3)Косинус угла между н. Отрезками

(4) Условие ортогональности векторов<=> условие перпендикулярности направленных отрезков: ab  (a,b)=0.

5) Единичные векторы  являются единичными направленными отрезками-ортами координатных осей OX, OY, OZ, причем

---------------------------------------------------------------

Пример, a=[1;2;3]^t; b=[1;0;-2]^t ==>

Задача. При каком значении параметра "x" вектор а ортогонален вектору с=[-1;0;x]^t ?

(a,c)= -1+20+3x=0 ==> x=1/3  a=[1;2;3]^t  c=[-1;0;1/3]^t.

§13. Векторное произведение в R³ и его свойства.

Пусть заданы два вектора:

Определение. Векторным произведением векторов называется вектор

Например,

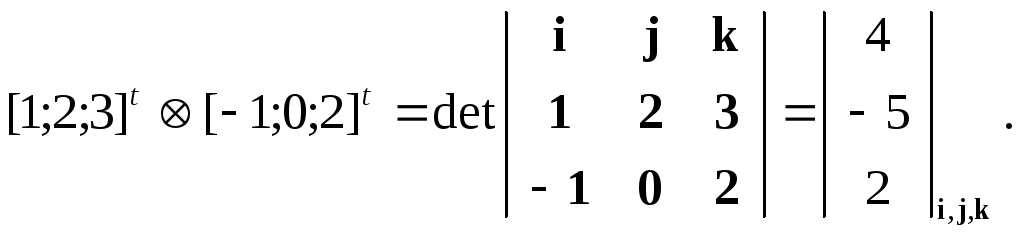
Свойства Векторного Произведения векторов.

(1). axb=-bxa <= перестановка строк в матрице.

(2). axa= ,<= две одинаковые строки в матрице;

(3). (a, axb)=

(b, axb)=0

Векторное произведение векторов ортогонально (перпендикулярно) сомножителям : aaxbb

(4). Можно показать, что норма векторного произведения векторов ||axb||=||a||||b|||sin(a,b)|=S равна площади параллелограмма, построенного на векторах a,b.

9