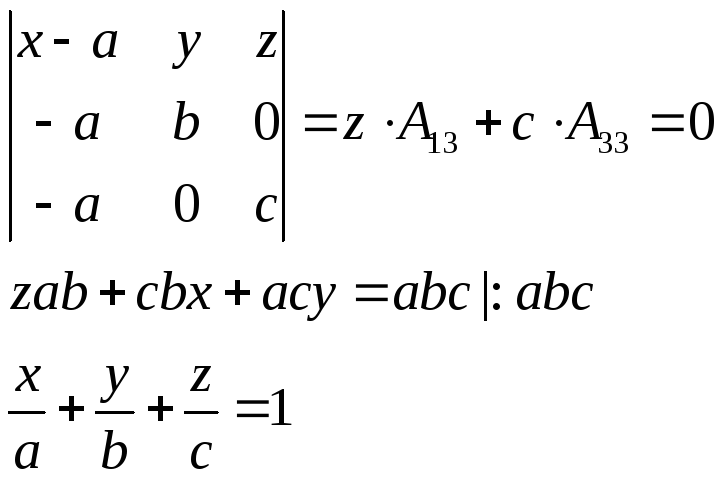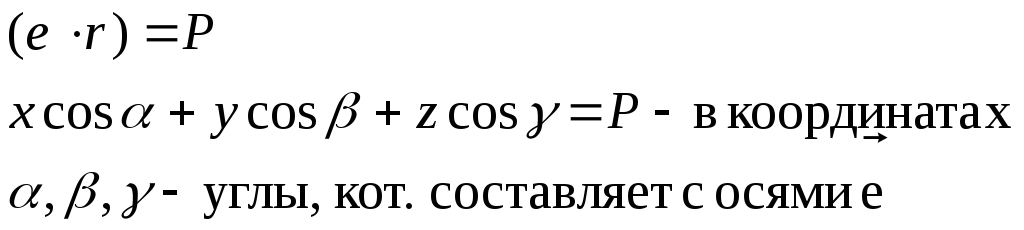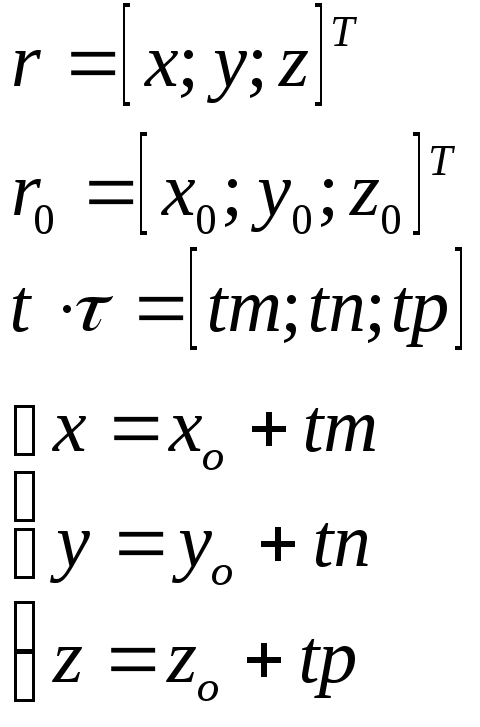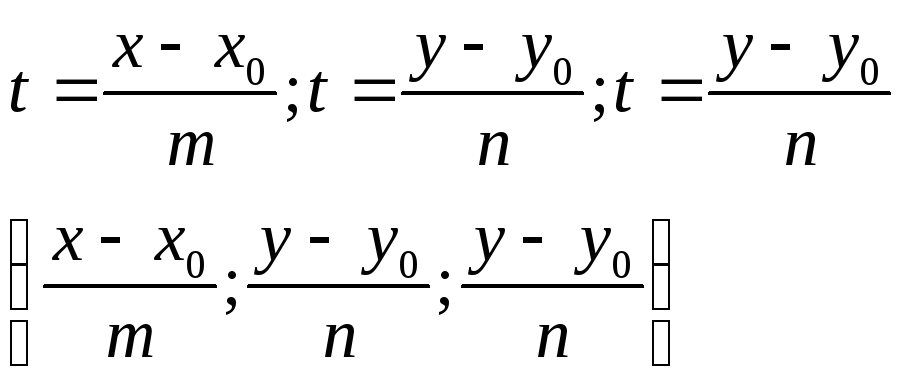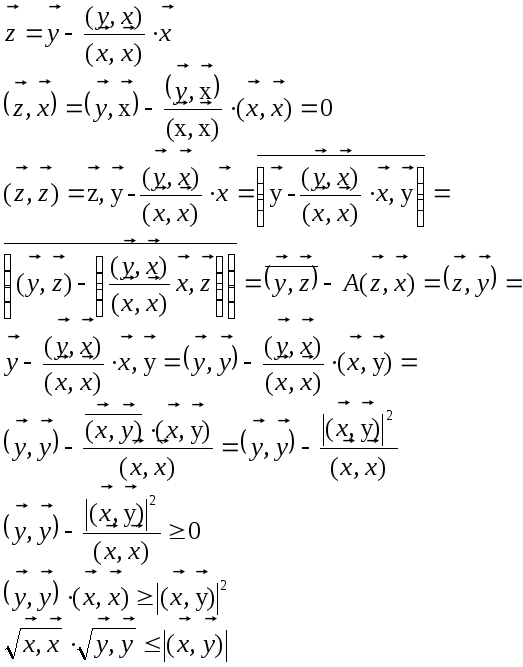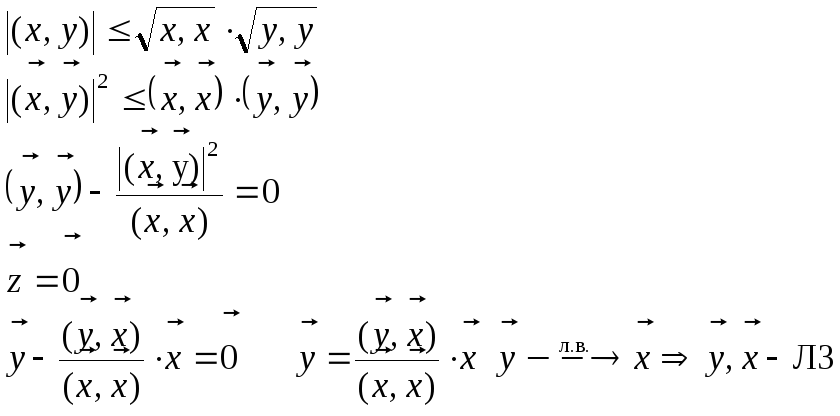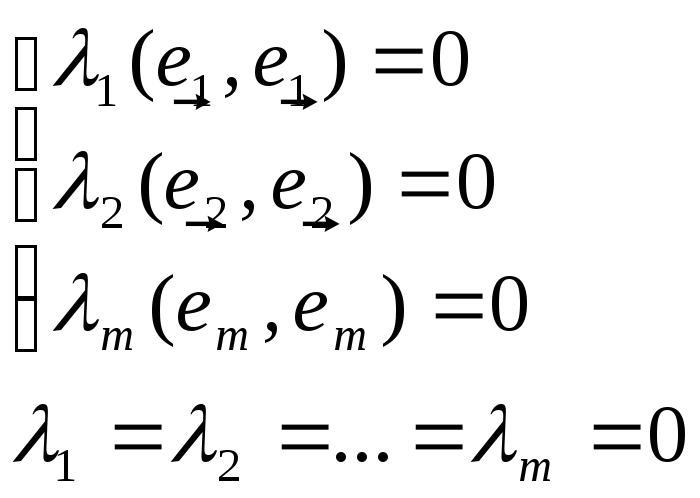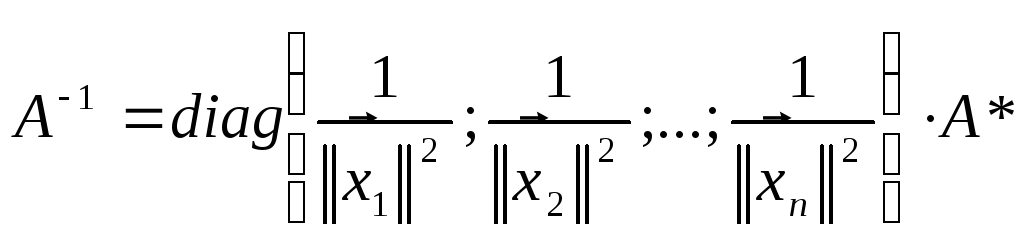Шпаргалка по линейной алгебре / 2008-04-16-23-25-Александра-
.doc|
1. Метод Гаусса-Жордана С помощью допустимых преобразований привести м-цу сис-мы к виду А или В, или убедиться, что она не совместна. Если появл. cтрока вида [0 0 0 … 0| b] то сис-ма не совместна. Алгоритм метода: 1. Переставляем строки, чтоб эл-т [1;1] был отличен от нуля. 2. Делим все эл-ты первой строки на этот эл-т. 3. Домножая строку на подх. множители и прибавляя её к остальным, обращаем в нуль все эл-ты первого столбца кроме 1-го. 4. Если появилась нулевая строка – вычеркиваем. 5. Если появ. [0 0 0 … 0| b], то сис-ма не совместна. И.Т.Д. Алгоритм заканчивается – 1) сис-ма несовместна, 2) вид А, 3) вид В. |
2. Определители. Определитель вводится только для квадратной м-цы. Определителем кв. м-цы А, называется её разложение по какому-либо столбцу или строке. Сумма произведений эл-тов i-той строки (k-того столбца) м-цы А, на соотв. им алгебраические дополнения называется разложением м-цы А по i-той строке (k-тому столбцу). Разложения кв. м-цы по любым строкам и столбцам совпадают.
Алгебраическим
дополнением
называется число определяемое рав-вом:
Минором i-той строки j-того столбца м-цы n-го порядка, называется определитель м-цы (n-1)-го порядка, которая получается из м-цы А путем вычеркивания i-той строки и j-того столбца. Свойства определителей: 1. Если кв. м-ца имеет нулевую строку или столбец, то ее определитель равен нулю. Лемма: Если поменять местами две соседние строки (столбца) то знак определителя изменится. Д-во: Написать два опред. Во втором поменять местами i и i+1 строки. Разложить 1-ый по i строке, а 2-ой по i, которая стала i+1. Замеч.: при четном числе перестановок сосед. строк, знак опред. не меняется, при неч. меняется. 2. Если поменять местами каке-нибудь две строки (столбца), то определитель изменит знак. Д-во: Переставим i строку на j место, посл. переставляя соседние строки... Всего потр. 2(j-i)–1 перестановок, неч. кол-во-опр. меняет знак 3. Если м-ца имеет 2 одинак. строки (столбца), то опред. равен нулю. Д-во: Поменяем местами две одинак. строки. Знак опред. изменится, но ничего не изменится. D=-D => D=0.
|
4. Сумма произведений эл-тов какой-либо строки (столбца) на соотв. алгебраические дополнения другой строки (столбца) равна нулю. Д-во: D отл. от D1 тем, что в D1 2 одинак. строки, все ост. такие же как у D. Раскл. D1 по j строке. Алгебр. дополнения не зависят от эл-тов, для которых они строятся.
Опр. D
и D1
отл. только j
строкой =>
5. Определитель
умножается на число
Д-во:
Разложить м-цу
по строке умнож. на
6. Если эл-ты некоторой строки кв. м-цы равны сумме двух слагаемых, то определитель этой м-цы равен сумме определителей двух м-ц, у одной их которых соответствующая строка состоит из первых слагаемых, а у второй из вторых. При этом остальные строки этих м-ц такие же как у исходной. Д-во: Алг. доп. не зависят от эл-тов для кот. они строятся!
7. Если к какой-нибудь
строке (столбцу) прибавить другую
строку (столбец) умнож. на
Д-во:
Из D
делаем D1
прибаляя к i-той
строке j-ю
умнож. на
8. Определитель произведения равен произведению определителей. |
|
3. Теорема Крамера. ОСЛАУ. Т| Если определитель системы отличен от 0, то данная система имеет единственное решение. Д-во: По Г-Ж. Т обр.| Если система имеет единственное решение, то ее определитель отличен от 0. Д-во Раз сис-ма имеет единств. решение, то алг. Г.-Ж. заканч. получением еденич. м-цы, опред. которой отличен от 0. Докажем от противн., что detА не равен 0. detА=0, но по Г-Ж. все преобразов. таковы, что опред. исх. м-цы равен опред. преобр => =0, что невозм. т.к. см. выше. ОСЛАУ ОСЛАУ всегда совместны, ибо есть хотя бы одно решнение – нулевое. Т| Если кол-во ур-ий в ОСЛАУ меньше кол-ва неизвестных, то она имеет бесконечно много решений. Д-во: По Г.-Ж.
Ф-ла Крамера Следствие пр. и обр. теорем Крамера. Пусть кол-во ур-ий равно кол-ву неизв. Тогда ОСЛАУ имеет единств. нулевое решение <=> det отличен от 0.
|
4. Обратная матрица.
Кв. м-ца Х n-го
порядка называется обратной
к А, если одновременно выполняются
два матричных рав-ва
Т| Если определитель кв. м-цы А равен нулю, то м-ца А необратима. Д-во: От противного. AX=E, det(AX)=det(E), detA detX=detE, 0 detX=1, 0=1, что невозможно. Т| Если определитель кв. м-цы отличен от 0, то для этой м-цы сущ-ет ей обратная, причем единственная. Д-во: 1) A X=E и 2) Y A=E имеют единств. решение и они равны между собой. 1 ур-ие СЛАУ имеющ. единств. решение => м-ца X опред. единств. образом. 2 ур-ие. (Y A)= E, A Y= E. Аналогично с 1. (A X)=E, Y (A X)=Y E, Y A X = Y, E X=Y, X=Y. Способ вычисл. эл-тов обр. м-цы. 1) det=0 => обр. м-ца существует. 2) Заменяем эл-ты м-цы А соотв. им алг. доп. 3) Траснпонируем получ. м-цу. 4) Делим каждый эл-т на detA. |
5. Линейная зависимость.
В-ры
В-ры
Лемма1
Для любого в-ра
1)
Для любого ч-ла
2)
Для любого в-ра
3)
Лемма2
В-ры
Д-во:
1) Пусть U1…Un
ЛЗ => сущ-ет ненулевой набор коэфф.
при кот. вып. рав-во *. Допустим, что
Лемма3
Д-во:
U1…Un,
V
ЛЗ => рав-во * вып. При ненулевом наборе
коэфф.
Теорема о 4х дост усл. лин. зависимости. 1) Если среди векторов U1…Un есть 0-вектор, то сис-ма U1…Un лин. зависима. Д-во: Запишем рав-во * снабдив 0-вектор ненулевым коэфф, а все остальные нулевыми коэффициентами и получаем, что U1…Un ЛЗ. 2) Если подсистема системы в-ров U1…Un ЛЗ, то и вся система ЛЗ. Д-во: Запишем рав-во * для подсистемы, снабдив ее эл-ты ненулевыми коэфф. Затем допишем оставшиеся эл-ты системы снабдив их нулями. Получаем рав-во * для всей сис-мы, выполн. при ненулевом наборе коэфф, 3) Пусть каждый эл-т системы векторов U1…Un лин. выр. через систему векторов V1…Vm, где m<n, тогда U1…Un ЛЗ (‘длинная система выр. через короткую’) 4) Пусть V1…Vn ЛЗ и каждый эл-т системы векторов U1…Un лин. выр. через V1…Vn, тогда U1…Un ЛЗ. Д-во: 1)V1…Vn – ЛЗ => по лемме2 Vn лин. выр. через V1…Vn-1. 2) U1…Un лин. выр. через V1…Vn. В каждое лин. выражение вместо Vn подставляем лин. выр. через V1…Vn-1. Группируем слагаемые с одинкаовым Vi и выносим Vi за скобки. В рез-те получим сис-му линейных выражений векторов U1…Un через V1…Vn, т.е. по 3 усл. U1…Un ЛЗ. |
|
6.Базис Система векторов образует базис в множ-ве M, если 1)V1,V2,…Vn – ЛНЗ система 2)любой вектор V M лин. выр. через V1…Vn Теорема о базисах: 1) Если V1…Vn – базис M, то любой вектор V единтсвенным образом линейно выражается через в-ры V1…Vn. Д-во: Допустим, что может быть два лин. выр. Приравняем их, вынесем одинак. Vi. Получим рав-во * для ЛНЗ сис-мы => коэфф. равны 0, т.е коэфф. первого выр-я равны коэфф. второго выр-я. 2) Если V1…Vn базис M и f1…fm базис М, то m=n Д-во: Допустим, что, к примеру, m>n. Тогда по 2 усл. опред. базиса f1…fm лин. выраж. По базису V1…Vn => по 3му усл лин. зависимости f1…fm ЛЗ, что невозможно. 3) Базис - максимальная по длине ЛНЗ система Д-во: Аналогично со 2м. 4) Если e1, e2 … en ЛНЗ система в М. V1…Vn – базис М => e1…en – базис множества М. Д-во: Берем вектор W M e1…en,W – ЛЗ, т.к. в противном случае более длинная ЛНЗ систему, чем базис. По лемме3 W лин. выраж. Через e1…en => по определению e1…en базис в М.
|
7. Скалярное, смешанное и векторное произведения векторов.
Скалярным
произведением
векторов a
и b
называется число, определяемое
равенством:
Свойства:
Два вектора называются ортогональными, если выполняется хотя бы 1 из 2х условий: 1) Хотя бы один вектор нулевой. 2) Оба вектора ненулевые и угол между ними -90’ (скалярное произведение равно нулю)
Проекцией вектора
a
на в-р и называется число, определяемое
рав-ом:
Векторным произведением 2х векторов a и b называется вектор c, кот. обладает след. 3мя св-вами:
3) если в-ры a и b неколлин. То они обр. правую тройку, т.е. кратчайший поворот от вектора a к b виден из конца вектора с против ч.с. Если колл. то их скалярн. произвед. равно нулю. |
Модуль векторного произведения двух неколлин. векторов, есть S параллелограмма построенного на этих векторах. Свойства ВП:
4) ixi=0, ixj=k, ixk=-j, jxi=-k, jxj=0, jxk=i, kxi=j, kxj=-i, kxk=0
Смешанное
произведение векторов это
число определяемое условием
Свойства СП: 1) если в-ры a,b,c компланарны то их СП=0 2) СП 3х векторов неизменно при циклических перестановка эл-тов.
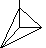
3) вычисл. формула
СП:
|
|
8. Плоскость и прямая Ур-ием (нер-вом) фигуры называется ур-ие (нер-воудовл. следующим двум условиям: 1) если точка принадлежит фигуре, то её координаты удовл. данному ур-ию (нер-ву). 2) если координата некоторой точки удовл. ур-ию (нер-ву), то точка принадлежит фигуре. Плоскость. 1) Общее ур-ие плоскости Ax+By+Cz+D=0 2) Ур-ие плоскости проходящей через точку x , y, z , перпендикулярно вектору n с коорд. (A,B,C,) A (x-x )+B(y-y )+C(z-z )=0 3) Ур-ие плоскости, прох. через 3 точки Даны М1 М2 М3. M (x,y,z) произвольная точка в пл-ти. M1М, М1M2, М1M3 – компланарны.
4) Ур-ие плоскости в отрезках.
О OB=b OC=c A=(a;0;0) B=(0;b;0) C=(0;0;c)
5) Нормальное ур-ие плоскости
Косинус угла между пл-тями: модуль косинуса угла между нормалями
Расст. от точки
до плоскости:
|
Прямая. 1) Векторное ур-ие прямой: OM=r; OMo=r; MoM r=r +MoM MoM || MoM=t ,t-число
2
3) Каноническое ур-ие прямой: Выразим из пар-р t
4
Mo (x0, y0, z0) M1 (x1, y1, z1) M l: M(x, y, z) MoM, MoM1 – коллин. MoM (x-x0; y-y0; z-z0) MoM1 (x1-x0; y1-y0;z1-z0)
5) Общее ур-ие прямой: Прямую можно задать, как пересечение двух плоскостей
Косинус угла между прямыми: модуль косинуса угла между направл. векторами.
|
|
|
9. Скалярное произведение в линейном пр-ве. |
Рав-во в нерав-ве Коши-Буняковского достигается тольком когда в-ры x и y линейно зависимы. Да, блядь, не поверишь, блядь, но это так!!! д-во
|
|
|
|
Линейное пр-во над R |
Линейное пр-во над C |
||
|
Скалярным умнож. назыв. отображение f |
|||
|
f: LxL→R |
f: LxL→R |
||
|
Будем обозначать значение отображения на паре векторов. (x,y) – скалярное произведение, причем выполнены след. аксиомы: |
|||
|
А1| (x,x)=0 <=>x=0 A2| (x,y)=(y,x) |
(x,x)>0 (x,y)=(y,x) |
||
|
A3| (x+y,z)=(x,z)+(y,z) |
|||
|
A4| ( \x,y)= \(x,y) |
|||
|
Линейное пространство L над R со скалярн. произведением называется Евклидовым. Линейное пространство L над С со скалярн. произведением называется Унитарным. |
|||
|
Свойства скалярного произведения |
|||
|
Евклидово |
Унитарное |
||
|
1) (x-y,z)=(x,z)-(y,z) 2) (x,y+z)=(x,y)+(x,z) |
|||
|
3) (x, \y)= \(x,y) |
(x, \y)= \(x,y) |
||
|
4) (x,y)=0 |
|||
|
В Евклидовом и Унитарном пространстве справедливо нер-во Коши-Буняковского:
Д-во: 1) x=0 нер-во тривиальное. 2) x≠0 введем в рассм. z |
|||
|
10. ОБ, ОНБ, коэфф. Фурье, алг Грама-Шмидта В унитарном (евклидовом) пространстве сис-ма ненулевых попарно ортогональных векторов (e1…em) - ЛНЗ. Д-во: Запишем рав-во * для сис-мы векторов e1…em
Обе части этого рав-ва умножим скалярно справа последовательно на векторы e1…em
Пусть L n-мерное евклидов(унитарное) пространство. Тогда сис-ма ненулевых попарно ортогональных векторов сост. из n-элементов явл. базисом. Д-во: из п.4 Т. о базисах и см. выше. e1…en- ОБ если при этом норма вектора равна 1, то он ОНБ. |
Пусть e1…en – ОБ. Возьмем x из L x=x1e1+x2e2+…xnen Скалярно умножим на e1…en обе части
Xi - коэфф. в-ра x в ОБ если e1…en – ОНБ, то Xi=(x,ei) Алгоритм Грама-Шмидта Дано: {a1…an} - базис
|
|
|
11. Собств. числа и собств. векторы f:L1→L1 f- оператор умн. вектора на число. f(x)= \x f(x)e=Ax e= \x e Пусть А – кв. мтарица. Если Ax= \x, где x≠0!!!, то число \ наз. собств. числом м-цы А, а x≠0 наз. собственным вектором м-цы А, соотв. собств. числу \.
матричная запись ОСЛАУ в, кот. кол-во ур-ий = кол-ву неизв.
Данная система
имеет ненул, решение, тогда, когда
det 1) Решить ХУ, найти СЧ 2)найдя СЧ подстав. в рав-во (€) решить эту сис-му методом Г.-Ж. и найти тем самым СВ. Т| СВ x1…xk кв. м-цы А, соответсвующ. разл собств. числам \1… \k, KYP
Д-во: По индукции
и приплести рав-во *, и еще умножить
там надо будет на
|
12. СЧ и CD самосопр. м-цы А* назыв сопряж. к А, если выполняется A*=A (транспон. и комплексно сопряж.) L-унит.(евкл.) пр-во А - м-ца ЛО в L, тогда (Ax,y)=(x,A*y) М-ца наз. самосопряженной, если А=А* Св-ва самосопряженной м-цы: 1) (Ax,y)=(x,Ay) 2) СЧ самосопр. матрицы действительные д-во: из Ax,x вычесть x,Ax. 3) СВ самосопр. м-цы соотв различным собств. числам ортогональны. д-во x-СВ \ у-СВ \ _Ax,y=( \ x,y)= \ (x,y) x,Ay=(x, \ y)= \ (x,y) 0 = (x,y)( \ , \ ) (x,y)=0 – x,y ортогональны. 4) Сущ-ет ровно n попарно ортогональных в-ров самосопр. м-цы и эти векторы образуют ортогон. базис в C ,R и этот базис наз. собств. базисом самосопр. м-цы
|
|
|
13. Унитарные м-цы. Кв. м-ца называется унитарной, если её столбцы образуют ортонормированный базис в С , R . T| М-ца унитарна тогда и только nulf когда м-ца обратная к А совп. с А*. Св-ва унитарной м-цы: |detA|=1 д-во: A* A=Е, det(A* A)=detE, detA* detA=1 detA detA=1 detA detA=1 (detA) =1 |detA|=1 2) (Ax,Ay)=(x,y) (Ax,Ay)=x,A*(Ay))=x,(A*Ay) 3)Унитарная матрица сохр. норму вектора ||Ax||=||x|| 4) CЧ унит. м-цы по модулю равны 1. \ - СЧ м-цы А x – СВ м-цы А, соотв \ (Ax,Ay)=( \x, \,x)= \ \ (x,x) \ \(x,x)=(x,x) \ \=1 | \|=1.
|
Приведение матрицы к диагональному виду. Пусть x1,x2,…,xn это попарно ортогон. ненулевые векторы. Расcм. м-цу А сост из столбцов А [x1…xn], тогда
д-во: М-ца А неявл. унитарной. нормируем x1…xn
|
|

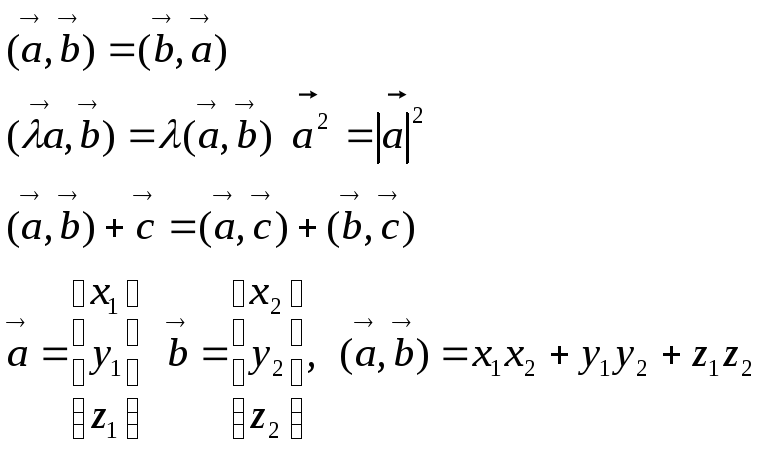

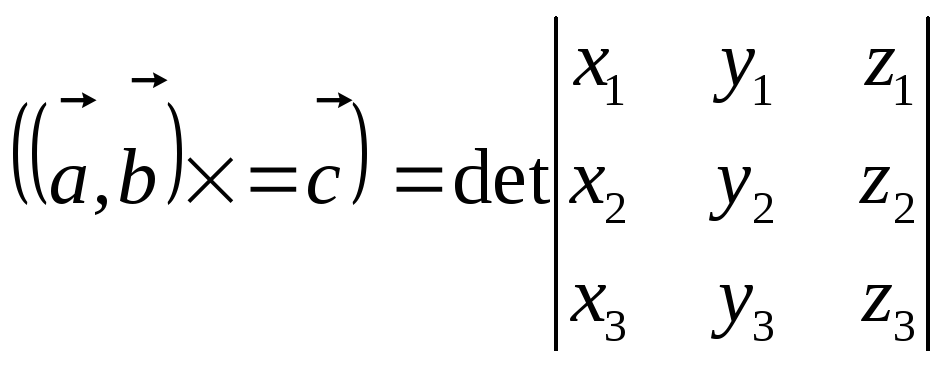

 А=a
А=a