Лекция № 9 Математика. Множества. Исследование функций

Множества.

Множеством называют определенную совокупность объектов. Понятие множества столь же первично как понятие точки или числа. Синонимами слова множество можно считать такие слова как совокупность, коллекция, семейство, собрание. Объекты, из которых составлено множество, называются элементами данного множества.

Нет никаких ограничений на природу элементов, составляющих множество. Например: различные предметы меблировки комнаты образуют множество. Множествами являются книги некоторой библиотеки, учащиеся класса, буквы алфавита, автомобили на дорогах города, целые числа от 1 до 1000 и т.д.

Множество, имеющее конечное число элементов, называется конечным. Все рассмотренные ранее примеры служат примерами конечных множеств.

Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Т.е. множество, не являющееся конечным является бесконечным множеством. Например, множество всех вещественных чисел бесконечно.

Уже рассмотренное нами множество натуральных чисел - бесконечное множество, поскольку нет такого натурального числа, которое равнялось бы числу его элементов.

Примеры некоторых числовых множеств:

- множество натуральных чисел, = {1,2,3,... };

- множество целых чисел, = {0,1,2,3,... }.

Множество, в котором нет ни одного элемента, называют пустым множеством. Например, множество летающих бегемотов пусто. Пустое множество обозначается .

Для обозначения множества используют заглавные буквы латинского алфавита, а в фигурных скобках через запятую выписывают его элементы. Пустое множество записывают как {}.

Конечное множество это такое множество, для которого существует натуральное число равное числу его элементов. Существует два способа задания конечных множеств. Можно либо дать полный перечень элементов этого множества, либо указать правило для определения того, принадлежит или нет рассматриваемому множеству данный объект. Первый способ называется перечислением множества, а второй - описанием. Для бесконечных множеств возможен лишь второй способ. Например, перечисление {2,4,6,8} или описание: "Четные числа, большие 0 и меньшие 10"; перечисление {вторник, среда, четверг} или описание: "Первый, второй и третий дни после понедельника".

В математике принято использовать следующие обозначения:

a  X - "элемент a принадлежит множеству X";

X  a - "множество X содержит элемент a", что, вообще говоря, то же самое;

a  X - "элемент a не принадлежит множеству X";

Множество, состоящее из некоторых элементов другого множества, называется его подмножеством. Считается, что пустое множество является подмножеством любого множества.

Например, множества {4,8} и {6} являются подмножествами множества {2,4,6,8}; числа 2, 4, 6, 8 - его элементы.

У любого множества есть обязательно хотя бы два подмножества: пустое множество и само множество. Эти два подмножества называются несобственными подмножествами. Любое подмножество, отличное от несобственного, называется собственным подмножеством данного множества.

Множества, состоящие из одних и тех же элементов, называются равными. При этом порядок перечисления элементов множества значения не имеет. Два конечных множества A и B будут равными, если они состоят из одних и тех же элементов. Если множества A и B равны, то мы будем писать A = B, в противном случае A  B. Например: равны множество равносторонних треугольников и множество равноугольных треугольников; равны множества {7,4,1}, {1,4,7} и {7,1,4}. А множество {7,2,4} не равно им.

Таким образом, мы получили следующее определение: Два конечных множества A и B не равны между собой, если в множестве A есть элемент не принадлежащий множеству B или наоборот.

Если множество A - конечное множество, то через A принято обозначать число его элементов и называть A мощностью множества A. Т.е. мощностью конечного множества (размером конечного множества) называют количество его элементов. Мощность пустого множества равна нулю.

Введем еще одно важное отношение между множествами - отношение включения.

Пусть A и B - какие-то два множества. Если любой элемент x множества A является элементом множества B, то говорят, что множество A является подмножеством множества B и обозначают этот факт следующим образом A  B или B  A.

Согласно сказанному, множество букв слова “жетон” является подмножеством множества букв слова “множества”, множество букв слова “нож” включается во множество букв слова “жетон”:

{Ж, Е, Т, О, Н}  {М, Н, О, Ж, Е, С, Т, В, А}

{Н, О, Ж}  {Ж, Е, Т, О, Н}

Подмножество A множества B, отличное от самого множества B и  называется собственным подмножеством. Это записывается следующим образом: A  B. Это, так называемое, "строгое" включение множества A в множество B.

Существуют несколько основных операций над множествами. С их помощью можно строить новые множества.

Определение: объединением множеств А и В называется множество, содержащее все элементы из А и все элементы из В.

Объединением любого множества с пустым является само это множество.

Объединение множеств обозначается знаком U.

Например, пусть A={5,7,9}, B={6,1}. Тогда C=A U B={1,5,6,7,9}.

Определение: пересечением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат обоим множествам.

Если в пересечении множеств элементов нет, то говорят, что они не пересекаются или что их пересечение - пустое множество. Пересечение любого множества с пустым является пустым множеством. Пересечение множеств обозначается знаком ∩.

Например, пусть A={4,5,7,9,10}, B={3,7,9}. Тогда C = A ∩ B = {7,9}.

Определение: разностью множеств А и В называется множество тех элементов из А, которые не принадлежат множеству В.

Если из любого множества A вычесть пустое множество, то результатом вычитания будет само множество A. Разность множеств обозначается знаком \.

Например, пусть A={1,3,5,6,7}, B={6}. Тогда C=A \ B={1,3,5,7}.

сли G={гусь, кот, утка, курица, индюк}, H={кот, утка}, то R=G\H={гусь, курица, индюк}.

Операции над множествами можно изобразить графически. Так, закрашенный участок на картинке показывает разность "A \ B" множеств A и B.

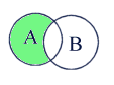
Подобные незамысловатые картинки называют диаграммами Венна, хотя еще раньше их применял известный математик Эйлер. Они очень удобны при работе с множествами и хорошо иллюстрируют соотношения между ними.

Исследования функций.

Две величины x, y связаны между собой функциональной зависимостью, если каждому значению одной переменной соответствует определенное значение для другой переменной. При этом та переменная, по которой отыскивается другая переменная, называется независимой переменной или аргументом, а другая является зависимой переменной или функцией.

Функциональная зависимость между двумя переменными может быть (точно или приближенно) выражена некоторой математической формулой. В тех случаях, когда функциональную зависимость трудно или невозможно представить с помощью формул, используются табличные или графические представления зависимости между двумя переменными.

Обозначение функции. Если известно, что переменная y есть некоторая функция переменной x , то независимо от способа задания этой функции устанавливается между двумя переменными функциональная зависимость в виде записи: y = f(x). Буква "f" это начальная буква латинского слова functio - функция.

Для графического изображения функциональной зависимости используют координатные оси. Две взаимно перпендикулярные прямые OX и OY образуют прямоугольную систему координат. Прямая "OX" обычно изображается горизонтально и называется осью абсцисс. Прямая "OY" изображается вертикально и называется осью ординат. Точка O - точка их пересечения - называется началом координат. На каждой из осей произвольно выбирается масштаб.

Каждой точке на плоскости, образованной координатными осями, соответствует одна пара чисел x и y. Каждой паре этих чисел соответствует на плоскости одна точка. Прямоугольная система координат часто называется декартовой, по имени французского математика и философа Декарта.

Для графического изображения функциональной зависимости двух переменных на оси абсцисс отмечаются ряд значений x1, x2, x3,..., а соответствующие им переменные y1, y2, y3, ..., отмечаются на оси ординат. На пересечении перпендикулярных прямых, исходящих из отмеченных на осях координат точек, получим график соответствующей функциональной зависимости.

Преимуществом графического изображения в сравнении с табличным является прежде всего его наглядность и легкая обозримость. Недостаток - малая точность. По графику можно найти значения функции для тех значений аргумента, которые отсутствуют в таблице. Нахождение промежуточных значений функции по ее графику называется графической интерполяцией.

Простейшие функции и их графики.

1. График линейной функции выражается уравнением вида y =Kx, где K - некоторая постоянная величина. Такая функция называется прямой пропорциональностью. Ее график есть прямая линия, проходящая через начало координат.

2. График прямой пропорциональности, переменные которой связаны уравнением

Y = Kx + B это прямая линия, отстоящая от начала координат на величину B.

3. Квадратичная функция выражается уравнением Y = Ax² +Bx +C, где A, B, C - постоянные величины. Кривая, служащая графиком квадратичной функции, есть парабола.

4. Показательная функция выражается уравнением Y=A^x, где A - постоянное положительное число.

5. Логарифмическая функция выражается уравнением Y = LOG_aX, где а - постоянное положительное число, не равное единице. Логарифмическая функция обратна показательной.

Основные понятия, связанные с функцией.

Область определения функции - все значения, которые принимает независимая переменная.

Область значений функции (множество значений) - все значения, которые принимает функция.

Функция является четной - если для любого х из области определения функции выполняется равенство f(x)=f(-x).

Функция является нечетной - если для любого х из области определения функции выполняется равенство f(-x)=-f(x).

Возрастающая функция - если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)<f(х₂).

Убывающая функция - если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)>f(х₂).

Вертикальные и наклонные асимптоты функции.

Рассмотрим функцию f(x), определенную на промежутке (а, b) (возможно, (a, b) = (-∞,∞), (a, b) = (a, ∞), (a, b) = (-∞, b)). Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения.

Если f(x₀) = 0, то график функции пересекает ось абсцисс в точке x₀.

Если 0 Є (a, b), ординат в точке y₀ = f(0).

Если в точке x₀ Є (a, b) функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту x = x₀ Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты x = x₀ стремиться к нулю при x → x₀ справа, слева или с обеих сторон.

Если (a, b) = (-∞, b), (a, b) = (a, ∞) или (a, b) = (-∞,∞), существуют и конечны пределы

и при x → ± ∞, то прямая y =kx+b - асимптота графика f(x).

Если lim f(x) = ± ∞ при x→ a+0, то график функции имеет на левой границе области сходимости вертикальную асимптоту ; аналогично, если lim f(x) = ± ∞ при x→ b-0 то график функции имеет на правой границе области сходимости вертикальную асимптоту x = b.

Если (a, b) = (-∞,∞) и существует число T ≠ 0, что f(x+T) = f(x) для любого x Є(-∞,∞) , то исследуемая функция периодична с периодом T; в этом случае достаточно построить график функции на промежутке (0, T) и доопределить его периодичность на всю числовую ось.

Если f(-x) = f(x), для всех x Є (-a, a), то исследуемая функция четная; в этом случае достаточно построить график функции на промежутке (0, a) и отобразить его симметрично относительно оси ординат на (-a, 0).

Если f(-x) = - f(x), для всех x Є (-a, a), то исследуемая функция четная; в этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке (0, a) и отобразить его симметрично относительно начала координат на (-a, 0).

Если функция дифференцируема на промежутке (a, b), за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения.

Для того, чтобы дифференцируемая на (a, b) функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы f'(x) >= 0 (f'(x) <= 0 ) на (a, b).

Пусть в точке x = x₀ производная f'(x₀) = 0 или не существует. Если существует окрестность точки x₀, такая, что для x из этой окрестности f'(x)>0 при x < x₀ и f'(x)<0 при x > x₀, то функция имеет в точке x₀ максимум. Если же f ' (x) < 0 при x < x₀ и f '(x) > 0 при x > x₀ , то функция имеет в точке x₀ минимум (в этом случае говорят, что производная меняет знак при переходе через точку x = x₀).

Если непрерывная в точке x₀ функция f(x) дифференцируема на (a, x₀) U (x₀ , b), при этом f'(x) > 0 на (a, x₀) и f '(x) < 0 на (x₀ , b) то функция имеет в точке x₀ максимум; если же f'(x) < 0 при x < x₀ и f'(x) > 0 при x > x₀, то функция имеет в точке x₀ минимум.

Если функция дважды дифференцируема на промежутке (a, b), за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.

График функции f (x) называется выпуклым (выпуклым вниз) на промежутке (а , b) , если он расположен выше касательной, проведенной в любой точке (x ,f(x)), x Є(a, b). Если же график функции лежит ниже касательной — то он называется вогнутым (выпуклым вверх).

Если дважды дифференцируемая на промежутке (а , b) функция f(x) имеет на нем положительную вторую производную, то функция выпуклая на (а , b). Если же вторая производная отрицательна на промежутке (а , b), то функция на нем вогнута.

Если вторая производная равна нулю в точке x = x₀ , а слева и справа от нее имеет значения разных знаков, точка x = x₀ — точка перегиба.

Лекция № 10. Элементы теории вероятностей. Математическая статистика

Элементы теории вероятности.

Теория вероятности возникла как наука из убеждения, что в основе массовых случайных событий лежат детерминированные закономерности. Теория вероятности изучает данные закономерности.

Например: определить однозначно результат выпадения “орла” или “решки” в результате подбрасывания монеты нельзя, но при многократном подбрасывании выпадает примерно одинаковое число “орлов” и “решек”. В этом состоит специфика вероятностных прогнозов, они справедливы лишь при достаточно большом количестве испытаний.

Испытанием называется реализация определенного комплекса условий, который может воспроизводиться неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которого в каждом испытании приводит к неоднозначности исхода испытания.

Например: испытание - подбрасывание монеты.

Результатом испытания является событие. Событие бывает:

Достоверное (всегда происходит в результате испытания);

Невозможное (никогда не происходит);

Случайное событие (может произойти или не произойти в результате испытания).

Например: При подбрасывании кубика невозможное событие - кубик станет на ребро, случайное событие - выпадение какой либо грани.

Конкретный результат испытания называется элементарным событием.

В результате испытания происходят только элементарные события.

Совокупность всех возможных, различных, конкретных исходов испытаний называется пространством элементарных событий. Совокупность элементарных событий это пространство элементарных событий.

Сложным событием называется произвольное подмножество пространства элементарных событий.

Сложное событие в результате испытания наступает тогда и только тогда, когда в результате испытаний произошло элементарное событие, принадлежащее сложному.

Таким образом, если в результате испытания может произойти только одно элементарное событие, то в результате испытания происходят все сложные события, в состав которых входят эти элементарные.

Например: испытание - подбрасывание кубика. Элементарное событие - выпадение грани с номером “1”. Сложное событие - выпадение нечетной грани.

Введем следующие обозначения:

А - событие;

 - элементы пространства ;

 - пространство элементарных событий;

U - пространство элементарных событий как достоверное событие;

V - невозможное событие.

Операции над событиями. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда, когда произошло событие, которое входит или в A или в B. Сумма произвольного количества событий состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.

Событие C называется произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.

Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.

События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания, т.е. они не имеют общих элементарных событий. В противном случае события будут совместными.

Относительная частота наступления события. Пусть пространство элементарных событий конечно и состоит из m элементарных событий. В этом случае в качестве возможных исходов испытаний рассматривают 2^m событий. Относительной частотой наступления события A в n испытаниях называется число

Теория вероятности используется при описании только таких испытаний, для которых выполняется следующее предположение: Для любого события A относительная частота наступления этого события в любой достаточно большой серии испытаний имеет одно и то же значение, которое называется вероятностью наступления события A и обозначается P(A). Следовательно, если рассматривается вероятность наступления произвольного события, то мы понимаем это число следующим образом: это относительная частота наступления события в бесконечной (достаточно длинной) серии испытаний.

Классическое определение вероятности. Пусть  состоит из конечного числа элементарных событий и все элементарные события равновероятны, т.е. ни одному из них из них нельзя отдать предпочтения до испытания, следовательно, их можно считать равновероятными. Тогда достоверное событие , где n - количество равновероятных событий. Очевидно . Пусть произвольное событие . Тогда , т.е. событие A состоит из k элементарных событий.

Если элементарные события являются равноправными, а, следовательно, и равновероятными, то вероятность наступления произвольного события равна дроби, числитель которой равен числу элементарных событий, входящих в данное, а знаменатель - общее число элементарных событий.

Таким образом, при классическом определении вероятность события определяется равенством P(A) = k/n, где k -, число элементарных исходов испытания благоприятствующих появлению события А, n - общее число возможных элементарных исходов испытания.

При решении вероятностных задач в тех случаях, когда применима формула классической вероятности, для подсчета чисел k и m можно воспользоваться формулами комбинаторики.

Напомним одну из основных формул комбинаторики. Число сочетаний из n элементов по k вычисляется по формуле: ; в этой формуле n! означает произведение всех натуральных чисел от 1 до n и читается "эн факториал": n! = 1*2*3*...*(n-1)*n. Многие задачи, в которых для подсчета числа элементарных исходов испытания используется формула числа сочетаний, могут быть сведены к абстрактной схеме, называемой "задачей с шарами".

Пусть в урне имеется n одинаковых шаров, из которых m - белые. Определить вероятность того, что среди выбранных наудачу k шаров r окажутся белыми (m < n , r ≤ k).

Общее число способов, которыми можно вынуть k шаров из n находящихся в урне, равно

C^k_n. Благоприятствующими среди них будут те, при которых из m белых шаров будут извлечены r (число способов равно C ^r_m) и после каждого из этих выборов из n - k черных будут извлечены m - r шаров (число способов равно C^m-r_n-m). Число способов, благоприятствующих рассматриваемому событию, равно и искомая вероятность находится по формуле классической вероятности:

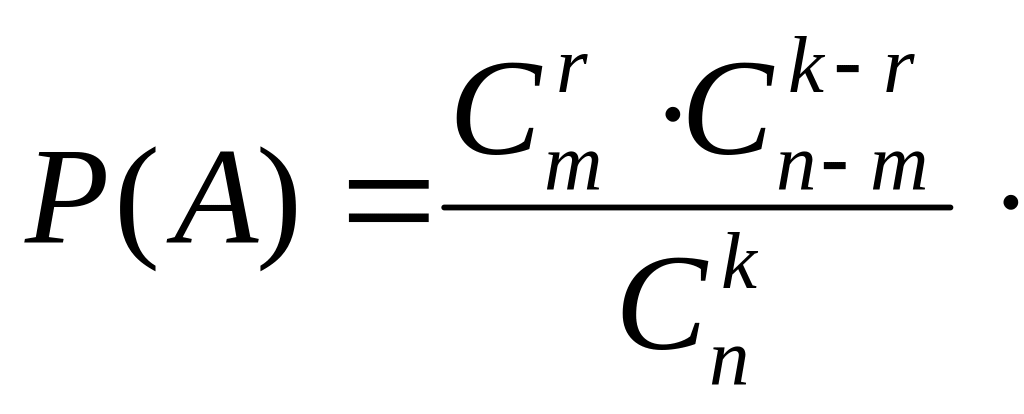
Теоремы сложения и умножения вероятностей.

Сложение вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B).

Сложение вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A + B) = P(A) + P(B) – P(AB).

Теорема может быть обращена на любое количество совместных событий. Например, для трех совместных событий: P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: P(AB) = P(A)•P_A(B).

В частности, для независимых событий P(AB) = P(A)•P(B), т.е. вероятность совместного появления двух независимых события равна произведению вероятностей этих событий.

Формула полной вероятности. Формула Байеса.

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) В1, В2, ..., Вn, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

P(A) = P(B1)•P_B1(A) + P(B2)•P_B2(A) +...+ P(Bn)•P_Bn(A), где P(B1) + P(B2) + ...+ P(Bn) = 1.

Первое равенство называют формулой полной вероятности.

Пусть событие А может наступить лишь при появлении одного из несовместных событий (гипотез) В1, В2, ..., Вn, образующих полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса

где P(A)=P(B1)•P_B1(A)+ P(B2)•P_B2(A) +...+ P(Bn)•P_Bn(A).

Повторение испытаний. Формула Бернулли.

Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна согласно формуле Бернулли

или где q = 1 - p.

Если производятся испытания, в которых n - велико, а p - достаточно мало, то вычисление по формуле Бернулли достаточно сложно. Тогда применяют формулу Пуассона

.

Локальная и интегральная теоремы Лапласа.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), приближенно равна (тем точнее, чем больше n) Здесь

Значения функции φ(x) можно определить по таблице Лапласа.

Интегральная теорема Лапласа.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна

Геометрическое определение вероятности.

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания очки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством Р = Длина l / Длина L.

Эти рассуждения можно распространить на плоские фигуры g , G и объемные фигуры v, V. Тогда получим следующие формулы определения геометрических вероятностей:

Р = Площадь l / Площадь L; Р = Объем v / Объем V.

Понятие случайной величины.

Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величина является одним из центральных понятий теории вероятностей.

Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M={1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной, она принимает значения из непрерывного числового множества - из отрезка числовой прямой.

Каждая случайная величина полностью определяется своей функцией распределения.

Если  - случайная величина, то функция F(x) = F_ (x) = P( < x) называется функцией распределения случайной величины . Здесь P( < x) - вероятность того, что случайная величина  принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

Итак, как дискретная, так и непрерывная случайные величины могут быть заданы функцией распределения F(x). Функция F(x) монотонно возрастает на всей числовой оси, причем, F(-∞) = 0, F(+∞) = 1. Плотностью или законом распределения случайной величины называют функцию f (x) = F' (x).

Если плотность распределения определяется формулой , то говорят, что случайная величина распределена по нормальному закону.

Для примера рассмотрим некоторые распределения дискретной случайной величины.

Биномиальное распределение.

Пусть проводится серия из n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”. Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q = 1- p. С таким испытанием можно связать случайную величину , значение которой равно числу успехов в серии из n испытаний. Эта величина принимает значения от 0 до n. Ее распределение называется биномиальным и определяется формулой Бернулли .

Геометрическое распределение.

Со схемой испытаний Бернулли можно связать еще одну случайную величину  - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до ∞ и ее распределение определяется формулой .

Гипергеометрическое распределение.

В партии из N изделий имеется M (M<N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначим ξ.

Распределение такой случайной величины называется гипергеометрическим и имеет вид

Числовые характеристики случайной величины.

Каждая случайная величина полностью определяется своей функцией распределения. В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины  обозначается M .

Математическое ожидание дискретной случайной величины  , имеющей распределение P(ξ) называется величина Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_ξ (x) вычисляется по формуле .

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина  имеет математическое ожидание M , то дисперсией случайной величины  называется величина D = M( - M )². Легко показать, что

D = M( - M )²= M ² - M( )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина M ² для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

Математическая статистика.

Рассмотрим предмет и основные понятия математической статистики. Обозначим количество всех подлежащих обследованию объектов N. . Допустим, что каждому i объекту (i=1,N), соответствует значение x_i. Cовокупность всех возможных значений (возможно даже домысливаемых ) N объектов называется генеральной совокупностью, а N – объемом генеральной совокупности. Генеральная совокупность может быть конечной или бесконечной. Пусть количество реально наблюдаемых объектов из N равно n. Тогда, x_i – выборка из генеральной совокупности, n – объем выборки. Выборка из генеральной совокупности должна обладать следующими свойствами:

• каждый элемент x_i выбран случайно;

• все x_i имеют одинаковую вероятность попасть в выборку;

• n должно быть настолько велико, насколько это позволяет решать задачу с требуемым качеством (выборка должна быть репрезентативной, представительной).

Принято считать, что при n ≥ 60 выборка большая, или репрезентативная, а при n < 60 – малая. Такое деление выборки на большую и малую условно.

Основная задача математической статистики состоит в определении свойств генеральной совокупности по выборке ограниченного объема n , используя по возможности априорные предположения.

К задачам математической статистики относятся следующие:

• разработка и применение методов оценивания числовых и функциональных характеристик генеральной совокупности по выборке из нее;

• описание эмпирических данных вероятностными моделями;

• проверка статистических гипотез;

• определение взаимосвязи между характеристиками исследуемых объектов, процессов, явлений;

• выявление согласия наблюдаемых (эмпирических) данных с теорией;

• принятие решений.

Задачи математической статистики состоят в разработке методов сбора, систематизации и обработки статистических данных для их удобного представления, интерпретации и формирования научных и практических выводов.

Вариационный и статистический ряды. Если закон распределения случайной величины ξ неизвестен, то его можно приближенно оценить опытным путем. С этой целью над величиной ξ проводят ряд независимых испытаний (измерений). Вся мыслимая (бесконечная) совокупность этих измерений называется, как было сказано выше, генеральной совокупностью, а каждый конкретный ряд измерений (x₁, x₂,...,x_n)называют простой случайной выборкой.

Если повторить измерения той же случайной величины ξ , то в силу наличия случайных ошибок мы получим несколько другие значения (x'₁, x'₂,...,x'_n). Поэтому сами измерения нужно рассматривать как случайные величины, распределенные по одному и тому же закону, совпадающему с законом распределения случайной величины ξ . Функцию распределения F(x)случайной величины ξ называют функцией распределения генеральной совокупности.

Если простую выборку упорядочить по возрастанию, то ее называют вариационным рядом. Если для каждого неповторяющегося элемента вариационного ряда x_i указать относительную частоту его появления p^*_i = m_i /n , то такой вариационный ряд называют статистическим рядом распределения случайной величины ξ . Здесь m_i – число повторений (абсолютная частота появления элемента), а n – общее число измерений, или объем выборки. Имея вариационный ряд, легко построить эмпирическую (статистическую) функцию распределения . Здесь m_x – число членов вариационного ряда, лежащих левее от x, а m_x / n – частота попадания выборочного значения левее x ; F_n(x) – ступенчатая неубывающая функция, заданная на всей числовой оси, со скачками в точках . Величина скачка равна частоте p^*_i . Поскольку сумма абсолютных частот , то сумма относительных частот . Можно доказать, что F_n(x) → F(x) при n → ∞. Отсюда ясно, что эмпирическую функцию распределения можно использовать как оценку теоретической функции распределения F(x) .

Числовые характеристики Генеральной и выборочной совокупности.

Точечные оценки. Наиболее часто применяемыми числовыми характеристиками случайной величины ξ являются начальные и центральные моменты различного порядка. Для дискретной случайной величины моменты порядка k определяются следующими формулами:

,

для непрерывной случайной величины :

.

Чаще всего используется первый начальный момент α₁=m_ξ, называемый математическим ожиданием случайной величины , и второй центральный момент μ₂=D_ξ, называемый дисперсией. Матожидание – это среднее значение случайной величины, его называют еще центром распределения, дисперсия характеризует разброс случайной величины относительно центра распределения. Часто вместо дисперсии используют среднее квадратичное отклонение .

Если закон распределения случайной величины неизвестен, то мы не сможем вычислить числовые характеристики. В этом случае их заменяют оценками, полученными как функции выборки x = (x₁, x₂,...,x_n). Всякую функцию f_n(x) от выборки называют статистикой. Подходящую статистику используют в качестве оценки числовой характеристики. Чаще всего оценками начальных и центральных моментов служат соответствующие выборочные начальные и центральные моменты: , , где Mx - выборочное среднее, являющееся оценкой математического ожидания .

Интервальные оценки. Методы, дающие оценку параметра в виде некоторого числа или точки на числовой оси называют точечными. Точечная оценка без указания степени точности и надежности не имеет практического значения, так как представляет собой только возможное значение случайной величины, т.е. сама точечная оценка является величиной случайной. Можно доказать, что в выборке объема n из генеральной совокупности, распределенной по нормальному закону N(a,σ) среднее выборочное Mx распределено также по нормальному закону . Интервальной называют оценку, которая определяется двумя числами - концами интервала, перекрывающего оцениваемый параметр. Доверительным называют интервал, который с заданной надежностью (вероятностью) γ покрывают заданный параметр.

Рассмотрим вычисление доверительного интервала при нормальном законе распределения. Интервальной оценкой (с надежностью γ) математического ожидания a нормально распределенного количественного признака X по выборочной средней x_в при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал

x_в - t(σ/ √n) < a < x_в + t(σ/ √n),

где t(σ/ √n) = δ - точность оценки, n - объем выборки, t - значение аргумента функции Лапласа Ф(t), при котором Ф(t) = γ/2.

При неизвестном σ (и объеме выборки n < 30)

x_в - t_γ (s/ √n) < a < x_в + t_γ (s/ √n),

где s - "исправленное" выборочное среднее квадратическое отклонение, t_γ - аргумент функции Лапласа определяется по статистической таблице по заданным n и γ , x_в = ∑n_ix_i / n ,

Метод корреляционного анализа.

Корреляция в математической статистике, вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия. Пример такого рода зависимости даёт корреляционная таблица. Из таблицы видно, что при увеличении высоты сосен в среднем растет и диаметр их стволов; однако сосны заданной высоты (например, 23 м) имеют распределение диаметров с довольно большим рассеянием. Если в среднем 23-метровые сосны толще 22-метровых, то для отдельных сосен это соотношение может заметным образом нарушаться. Статистическая корреляция в обследованной конечной совокупности наиболее интересна тогда, когда она указывает на существование закономерной связи между изучаемыми явлениями.

Наиболее употребителен при измерении степени зависимости коэффициент корреляции ρ между X и Y

.

Коэффициент корреляции всегда -1≤ ρ ≤1. Практическое использование коэффициента корреляции в качестве меры зависимости оправдано лишь тогда, когда совместное распределение пары (X, Y) нормально или приближенно нормально.

Корреляционный анализ, совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между двумя случайными признаками или факторами. Корреляционный анализ экспериментальных данных заключает в себе следующие основные практические приёмы: 1) построение корреляционного поля и составление корреляционной таблицы; 2) вычисление выборочных коэффициентов корреляции или корреляционного отношения; 3) проверка статистической гипотезы значимости связи. Дальнейшее исследование заключается в установлении конкретного вида зависимости между величинами с помощью регрессионного анализа.

Метод регрессионного анализа.

Регрессия в теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости у = f(х), когда каждому значению независимой переменной х соответствует одно определённое значение величины у, при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины у.

Регрессионный анализ, раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным. Цель регрессионного анализа состоит в определении общего вида уравнения регрессии, построении оценок неизвестных параметров, входящих в уравнение регрессии, и проверке статистических гипотез о регрессии.

Если двумерное распределение X и Y нормально, то линия регрессии Y по X задается уравнением прямой y = m_y+ β_y(x - m_x), где β_y = ρ(σ_x/σ_y) - именуется коэффициентом регрессии.

Регрессионный анализ является одним из наиболее распространённых методов обработки результатов наблюдений при изучении зависимостей в физике, биологии, экономике, криминологии, технике и др. областях.

Проверка статистических гипотез.

Статистическая проверка гипотез - система приёмов в математической статистике предназначенных для проверки соответствия опытных данных некоторой статистической гипотезе. Процедуры статистической проверки гипотез позволяют принимать или отвергать статистические гипотезы, возникающие при обработке или интерпретации результатов измерений во многих практически важных разделах науки и производства, связанных с экспериментом. Правило, по которому принимается или отклоняется данная гипотеза, называется статистическим критерием.

Построение критерия определяется выбором подходящей функции Т от результатов наблюдений, которая служит мерой расхождения между опытными и гипотетическими значениями. Эта функция, являющаяся случайной величиной, называется статистикой критерия, при этом предполагается, что распределение вероятностей Т может быть вычислено при допущении, что проверяемая гипотеза верна. По распределению статистики Т находится значение Т₀, такое, что если гипотеза верна, то вероятность неравенства T >T₀ равна α, где α — заранее заданный уровень значимости.