
4 семестp / Методы / Измерения_2 / Izmereniya_2
.pdfМосковский государственный технический университет им. Н.Э. Баумана
Л.К.Мартинсон, Е.В.Смирнов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
ПО КУРСУ ОБЩЕЙ ФИЗИКИ
РАЗДЕЛ “ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН В КВАНТОВЫХ СИСТЕМАХ”
Под редакцией Л.К.Мартинсона
Издательство МГТУ им. Н.Э. Баумана
2001
Рецензент:
Мартинсон Л.К., Смирнов Е.В. Методические указания к решению задач по курсу общей физики: Раздел “Измерение физических величин в квантовых системах”/Под ред. Л.К.Мартинсона. - М.: Изд-во МГТУ им.
Н.Э.Баумана, 200_, ____ с.
Содержится краткий обзор основных понятий и соотношений теории, необходимых для решения задач по одному из разделов квантовой механики. Изложена методика решения типовых задач.
Для студентов II курса всех специальностей.
2
I. ПОСТУЛАТЫ КВАНТОВОЙ МЕХАНИКИ
Квантовая механика принципиально отличается от классической механики в подходе к вопросу о результатах измерения физических величин в квантовых системах.
Прежде всего, в квантовой механике физическая величина может иметь дискретный спектр значений, тогда как в классической механике все физические величины изменяются непрерывно.
Кроме того, результаты измерения в квантовой системе имеют вероятностный характер. Это означает, что в общем случае в процессе измерения наблюдаемой физической величины в квантовой системе с определенной вероятностью может реализоваться одно из нескольких возможных значений этой величины. Говорят, что в таком квантовом состоянии физическая величина не имеет определенного значения. В этом случае, зная волновую функцию, описывающую квантовое состояние, мы должны уметь предсказывать среднее значение наблюдаемой физической величины, полученное из ряда измерений.
Такой подход к вопросу о результатах измерения наблюдаемых физических величин в квантовой механике базируется на представлении физических величин операторами и разработке адекватного математического аппарата.
Сформулируем основные постулаты квантовой механики:
I. Каждому состоянию квантовой системы соответствует волновая функция Ψ (x, y, z, t), определяющая это состояние. Волновая функция нахо-
дится из решения уравнения Шредингера.
II. Каждой наблюдаемой физической величине f в квантовой механике ставится в соответствие некоторый линейный самосопряженный (эрмитов)
оператор Φˆ , действие которого на волновую функцию задается при его оп-
3
ределении. Соотношения между квантовомеханическими операторами аналогичны соотношениям, связывающим в классической механике соответствующие физические величины.
III. Единственным возможным результатом измерения наблюдаемой физической величины f может быть только собственное значение fn соответ-
ствующего ей оператора Φˆ .
Собственные значения оператора Φˆ находятся из решения уравнения
Φˆ Ψ n = fn Ψ n . |
(1.1) |
Это уравнение имеет набор собственных функций Ψ |
n и собственных значе- |
ний fn. В случае дискретного спектра физической величины этот набор представляет собой счетное множество (n=1, 2, ...).
Система собственных функций оператора любой физической величины представляет собой полную ортонормированную систему функций. Поэтому любую волновую функцию Ψ всегда можно разложить в ряд по таким собст-
венным функциям: |
|
|
Ψ = ∑ CΨn |
n , |
(1.2) |
n |
|
|
причем коэффициенты этого разложения можно определить по формуле |
||
C n = ∫ Ψ Ψn |
dV . |
(1.3) |
R N |
|
|
Здесь интегрирование ведется по всей области RN изменения пространствен- |
||
ных переменных размерности N. При использовании декартовой системы |
||
координат в одномерных задачах dV=dx для N=1, в двумерных |
задачах |
|
dV=dxdy для N=2 и в трехмерных задачах dV=dxdydz для N=3. |
|
|
Если для некоторого квантового состояния волновая функция Ψ |
не яв- |
|
ляется собственной функцией оператора Φˆ , то в этом квантовом состоянии физическая величина f не имеет определенного значения. Вероятность Pn то-
4

го, что при измерении физической величины f в этом квантовом состоянии будет получено численное значение fn, находится по формуле
P |
= |
|
C |
n |
|
2 |
, |
(1.4) |
|
|
|||||||
n |
|
|
|
|
|
|
|
а среднее значение (математическое ожидание) физической величины по результатам большого числа измерений можно определить как
f = ∑ |
Pn fn = ∫ Ψ (Φˆ Ψ )dV . |
(1.5) |
n |
RN |
|
Необходимым и достаточным условием возможности одновременного точного измерения двух физических величин a и b является коммутатив-
ность соответствующих им операторов |
ˆ |
ˆ |
|
||
A и |
B , то есть выполнение равенства |
||||
ˆ |
ˆ |
ˆ ˆ |
ˆ ˆ |
0 . |
(1.6) |
[A, B]≡ |
AB − |
BA = |
|||
ˆ ˆ |
двух операторов не равен нулю, то соответ- |
||||
Если же коммутатор [A, B] |
|||||
ствующие им две физические величины не могут быть измерены одновременно и точно. Для таких физических величин справедливы соотношения неопределенностей вида ∆ a∆ b > 0, утверждающие что обе неопределенно-
сти ∆ a и ∆ b не могут одновременно стремиться к нулю.
5
II. ПРЕДСТАВЛЕНИЕ ФИЗИЧЕСКИХ ВЕЛИЧИН ОПЕРАТОРАМИ
Приведем выражения для операторов основных физических величин квантовой механики:
Операторы координат. Действие этих операторов на волновую функцию сводится к умножению ее на координату. В операторной форме это можно записать в виде равенств
xˆ = x , yˆ = y , zˆ = z . |
(2.1) |
Отметим, что операторами умножения на соответствующие координаты являются также операторы координат в цилиндрической и сферической системах координат.
Операторы проекций импульса. Эти операторы связаны с дифференцированием по соответствующим координатам, причем
ˆ |
! |
∂ |
|
ˆ |
! |
∂ |
|
ˆ |
! |
∂ |
|
|
|
∂ x |
, |
∂ y |
, |
∂ z . |
(2.2) |
||||||||
px = − i |
|
py = − i |
|
pz = − i |
|
||||||||
Используя известное соотношение классической механики, можно построить оператор квадрата импульса по правилу
ˆ |
2 |
|
ˆ |
|
) |
2 |
|
ˆ |
|
) |
2 |
|
ˆ |
|
) |
2 |
|
|
!2 |
|
∂ |
2 |
|
∂ |
2 |
|
∂ |
2 |
(2.3) |
||||||
|
= |
|
|
+ |
|
|
+ |
|
|
= |
− |
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|||||||||||
p |
|
( p |
|
(p |
|
( p |
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
z |
|
|
|
|
|
|
|
|
∂ |
x |
|
∂ |
y |
|
∂ |
z |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или, используя оператор Лапласа, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
2 |
= |
− |
!2 |
∆ . |
|
|
|
|
|
|
|
|
|
|
|
(2.4) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Операторы проекций момента импульса. С использованием классической
формулы для момента импульса материальной точки |
" |
" " |
L = [r, p] , можно по- |
||
строить операторы проекций момента импульса по правилам
6

ˆ |
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
Lx |
= yˆpˆ z − |
zˆpˆ y |
= − i! |
y |
|
∂ z |
− |
z |
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||||
ˆ |
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
Ly |
= zpˆˆ x − |
xpˆ ˆ z = − i! |
z |
∂ x |
− |
x |
∂ |
|
. |
(2.5) |
||||
|
|
|
|
|
|
|
z |
|
||||||
ˆ |
|
|
|
|
|
∂ |
|
|
|
∂ |
|
|
|
|
Lz |
= xˆpˆ y − |
yˆpˆ x |
= − i! |
x |
∂ y |
− |
y |
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||
В сферической системе координат
ˆ |
|
|
|
|
∂ |
|
|
|
|
∂ |
|
|
||
Lx |
= |
− i! sinϕ |
∂θ |
+ |
ctgθ |
cosϕ |
∂ϕ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
ˆ |
|
|
|
|
∂ |
|
|
|
|
∂ |
|
|
||
Ly |
= |
− i! cosϕ |
|
∂θ |
|
− |
ctgθ |
sinϕ |
∂ϕ |
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
||||
ˆ |
= |
− i! |
|
∂ |
|
|
|
|
|
|
|
|
|
|
Lz |
|
∂ϕ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оператор Lz имеет дискретный спектр собственных значений |
||||||||||||||||||||||||||||
Lz |
= mh, где m=0, ± |
1, ± 2, ... |
|
|
|
|
||||||||||||||||||||||
каждому из которых соответствует собственная функция |
||||||||||||||||||||||||||||
|
|
|
Ψ |
m (ϕ ) = |
1 |
|
|
eimϕ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эти собственные функции ортонормированы, так что |
|
|||||||||||||||||||||||||||
|
2π |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
ecли n = |
m |
||||||
|
|
∫ Ψ |
|
|
|
|
n(ϕ |
) |
ϕd |
|
= |
|
|
|
|
|
|
|||||||||||
|
|
m (ϕΨ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
ecли n ≠ |
m |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для оператора квадрата момента импульса |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
∂ |
|
|
2 |
|
|
ˆ2 |
|
ˆ2 |
|
ˆ2 |
|
ˆ2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
L |
= Lx |
+ |
Ly + |
Lz |
= − ! |
|
|
z |
∂ y |
− |
y |
|
∂ |
|
|
+ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.9) |
|
|
|
|
|
|
|
|
2 |
|
y |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
+ |
|
∂ |
− |
|
∂ |
|
|
+ |
∂ |
|
− x |
∂ |
|
|
. |
|
|
|
|
|||||||||
x |
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
∂ z |
|
|
∂ x |
|
|
|
|
∂ x |
|
|
|
∂ |
y |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В сферической системе координат оператор Лапласа |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
∆ |
= ∆ |
|
|
r+ |
|
|
∆ |
|
|
|
Θ ,ϕ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
||
может быть записан с выделением его радиальной части
(2.6)
(2.7)
(2.8)
7
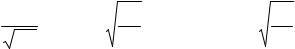
|
|
∆ r |
= |
1 |
|
|
∂ |
|
|
r |
2 |
|
∂ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
r |
2 ∂ |
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|||||||||
и угловой части |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∂ |
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
1 |
|
|
∂ 2 |
||||
∆ θ ,ϕ |
= |
|
|
|
|
sinθ |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
. |
||||||
sinθ |
∂θ |
|
|
∂θ |
|
|
sin |
2 |
θ |
|
∂ϕ |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В таких обозначениях оператор квадрата момента импульса в сфериче- |
|||||||||||||||||||||||||||
ской системе координат преобразуется к виду |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
ˆ2 |
|
|
2 |
∆ |
|
θ ,ϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
(2.10) |
||||||
|
|
L = |
|
− ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Спектр собственных значений оператора |
|
ˆ2 |
является дискретным |
||||||||||||||||||||||||
L |
|
||||||||||||||||||||||||||
L2 |
= !2l(l + |
1) , |
|
l=0, 1, 2, .... |
|
|
|
(2.11) |
|||||||||||||||||||
причем каждому собственному значению с заданным значением l соответст-
вуют (2l + 1) собственных функций Ψ lm=Ylm(Θ ,ϕ ), отличающихся значениями целочисленного параметра m=0, ± 1, ± 2, ..., ± l. Каждому значению m соответ-
ствуют определенные значения проекции момента импульса Lz, которые определяются формулой (2.7).
Функции Ylm(Θ ,ϕ ) называются шаровыми или сферическими функция-
ми. Приведем явный вид нескольких первых нормированных сферических
функций: |
|
|
|
|
|
|
|
|
|
Y0,0 = |
1 |
, |
Y1,0 |
= |
3 cosθ , Y1,± |
1 = |
3 |
sin θ e± iϕ . |
(2.12) |
|
4π |
|
|
|
4π |
|
8π |
|
|
Эти функции нормированы условием |
|
|
|
|
|||||
|
|
|
2π |
π |
|
|
|
|
|
|
|
|
∫ |
∫Yl,*mYl,m sin θ dθ dϕ |
= |
1. |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
Операторы энергий.
Оператор кинетической энергии определим, пользуясь классической формулой связи кинетической энергии частицы массы m0 и ее квадрата им-
8
пульса: EK = |
p2 |
. Аналогичное соотношение связывает операторы в кван- |
||||||
2m0 |
||||||||
|
|
|
|
|
|
|
||
товой механике. Поэтому, с учетом (2.4), получаем |
|
|||||||
|
|
ˆ |
pˆ 2 |
!2 |
|
(2.13) |
||
|
|
EK = |
|
= − |
|
∆ |
||
|
|
2m |
2m |
|||||
|
|
|
0 |
0 |
|
|
||
Оператор потенциальной энергии представляет собой оператор умножения на функцию U=U(x, y, z), определяющую потенциальную энергию частицы в стационарном силовом поле, то есть
ˆ |
(2.14) |
U = U (x, y, z) . |
|
Оператор полной энергии в квантовой механике называют оператором |
|
функции Гамильтона или просто гамильтонианом. |
Гамильтониан |
$ |
|
|
|
|
|
|
|
H определяется как сумма операторов кинетической и потенциальной энер- |
|||||||
гий и имеет вид |
|
|
|
|
|
|
|
ˆ |
ˆ |
ˆ |
!2 |
|
+ U (x, y, z) . |
(2.15) |
|
H = |
EK + U = |
− |
2m |
∆ |
|||
|
|
|
0 |
|
|
|
|
Выражение (2.15) можно использовать и в случае нестационарных си- |
|||||||
|
ˆ |
= U (x, y, z, t) |
силовую функцию, связанную с си- |
||||
ловых полей, понимая под U |
|||||||
"
лой, действующей на частицу, соотношением F = − U .
9

III. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Докажите, что оператор проекции импульса pˆ x является ли-
нейным самосопряженным (эрмитовым) оператором.
Решение. Линейность оператора pˆ x = − i! ∂∂x ≡ !i ∂∂x очевидна, поскольку дифференцирование является линейной операцией. Покажем, что оператор
px является эрмитовым оператором, |
то есть для него выполняется условие |
||||||
ˆ |
|
|
|
|
|
|
|
самосопряженности |
|
|
|
|
|
|
|
∫ |
* |
ˆ |
∫ Ψ |
ˆ |
* |
dV . |
(3.1) |
Ψ 1 |
(px Ψ 2 )dV = |
2( px Ψ 1) |
|
||||
RN |
|
|
RN |
|
|
|
|
Здесь Ψ 1 и Ψ 2 - две произвольные функции, для которых выполнены все ус-
ловия, накладываемые на волновые функции. В частности, эти функции должны обращаться в нуль вместе с производными на границе рассматриваемой области.
Для упрощения выкладок ограничиваемся рассмотрением одномерного случая, когда функции Ψ 1 и Ψ 2 зависят только от одной пространственной координаты x. Тогда имеем
+∞ |
* |
ˆ |
|
|
! |
|
+∞ |
* |
|
∂ Ψ 2 |
|
|
|
|
! |
|
* |
|
+∞ |
|
|
! |
+∞ |
|
∂ Ψ 1* |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
I = ∫ |
Ψ 1 |
= |
|
|
|
∫ |
|
Ψ |
1 |
|
d x = |
|
Ψ |
1 Ψ 2 |
|
|
|
|
+ i |
∫ Ψ |
2 |
|
d x . |
|||||||||
(px Ψ 2 )d x |
|
i |
|
|
|
∂ |
x |
i |
|
− ∞ |
|
∂ x |
||||||||||||||||||||
− ∞ |
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
− ∞ |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Поскольку по условию Ψ 1(m∞) |
|
=Ψ |
|
|
2( m∞) |
= |
|
0, то |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
+∞ |
|
2 |
|
∂ Ψ |
* |
|
|
|
|
|
+∞ |
|
|
|
|
∂ Ψ * |
|
|
|
|
|
|
|
||||||
|
|
|
∫ |
|
|
|
|
|
1 |
|
|
|
|
|
∫ |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
I = i! |
|
Ψ |
|
|
|
|
∂ x |
|
d x = |
|
Ψ |
|
|
i! |
∂ x |
|
|
d x = |
|
|
|
|
||||||||
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
+ ∞ |
|
|
|
|
|
|
|
∂ |
Ψ |
1 |
|
* |
|
|
|
+ ∞ |
2 (pˆ x Ψ |
1) |
* |
|
|
|
|
|
|
|||||
|
|
= ∫ Ψ |
2 |
− i! |
|
|
|
|
|
|
d x = |
|
∫ |
Ψ |
|
d x. |
|
|
|
|
||||||||||||
|
|
|
|
∂ x |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, показано выполнение условия самосопряженности
+∞ |
+∞ |
∫Ψ 1* (pˆ x Ψ 2 )d x. = ∫ Ψ 2( pˆ x Ψ 1) * d x |
|
− ∞ |
− ∞ |
для оператора проекции импульса.
10
