
- •Вопрос №1. Перемещение, скорость, путь, ускорение. Вычисление пройденного пути при равномерном и равноускоренном прямолинейном движении.
- •Вопрос №2. Криволинейное движение. Нормальное и тангенциальное ускорения. Кривизна траектории.
- •Вопрос №7. Работа и мощность. Поле сил. Консервативные и неконсервативные силы.
- •Вопрос №8. Потенциальная энергия. Потенциальное поле сил. Связь между потенциальной энергией и силой. Потенциал.
- •Вопрос №9. Кинетическая энергия. Закон сохранения механической энергии
- •Вопрос №10. Закон всемирного тяготения. Космические скорости.
- •Вопрос №11. Силы инерции
- •Вопрос № 12. Момент силы и момент импульса, их запись в векторном виде. Момент пары сил
- •Вопрос № 13. Закон сохранения момента импульса. Уравнение моментов.
- •Вопрос № 17. Свободные оси вращения твердого тела. Гироскопы. Прецессия
- •Вопрос № 18. Гармонические колебания. Уравнение свободных колебаний и его решение. Скорость и ускорение колеблющейся точки. Энергия гармонического колебания.
- •Вопрос № 20. Графическое изображение гармонических колебаний. Сложение колебаний одинакового направления. Биения.
- •Вопрос № 23. Вынужденные колебания. Резонанс. Резонансные кривые.
- •Вопрос № 30.Температура. Температурные шкалы. Теплоемкость и внутренняя энергия идеального газа. Теплоемкости Ср и Сv.
Вопрос № 17. Свободные оси вращения твердого тела. Гироскопы. Прецессия
Для того чтобы сохранить положение оси вращения твердого тела с течением времени неизменным, используют подшипники, в которых она удерживается. Но существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Можно показать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями – они называются главными осями инерции тела. Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Наиболее интересны в этом отношении гироскопы – массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью. Гироскопы применяют в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т.д.), а также в различных автопилотах. Прецессия — явление, при котором момент импульса тела меняет своё направление в пространстве под действием момента внешней силы.
Вопрос № 18. Гармонические колебания. Уравнение свободных колебаний и его решение. Скорость и ускорение колеблющейся точки. Энергия гармонического колебания.
Колебаниями
называются движения или процессы,
которые характеризуются определенной
повторяемостью во времени.
Колебания
называются свободными (или собственными),
если они совершаются за счет
первоначально сообщенной энергии при
последующем отсутствии внешних
воздействий на колебательную систему
(систему, совершающую колебания).
Простейшим типом колебаний являются
гармонические колебания — колебания,
при которых колеблющаяся величина
изменяется со временем по закону синуса
(косинуса). Энергия гармонических
колебаний : Кинетическая:
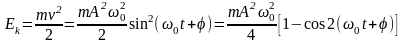 б) Потенциальная
энергия
материальной точки, совершающей
гармонические колебания под действием
упругой силы F, равна:
б) Потенциальная
энергия
материальной точки, совершающей
гармонические колебания под действием
упругой силы F, равна:
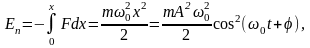
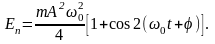 Полная энергия:
Полная энергия: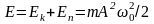
Скорость
колеблющейся точки:
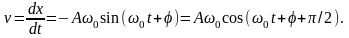 Ускорение
колеблющейся точки:
Ускорение
колеблющейся точки: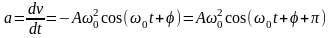
Вопрос № 19. Математический, пружинный и физический маятники. Приведенная длина физического маятника. Центр качаний.
Математический маятник— это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс тела. Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Центр качаний физического маятника, точка на перпендикуляре к оси подвеса, проходящем через центр масс маятника, которая расположена по ту же сторону от оси, что и центр масс, и отстоит от оси подвеса на расстоянии приведённой длины физического маятника l0. Величина l0 = I/Ml, где М — масса маятника, l — расстояние от его центра масс до оси подвеса, I — Момент инерции маятника относительно этой оси
