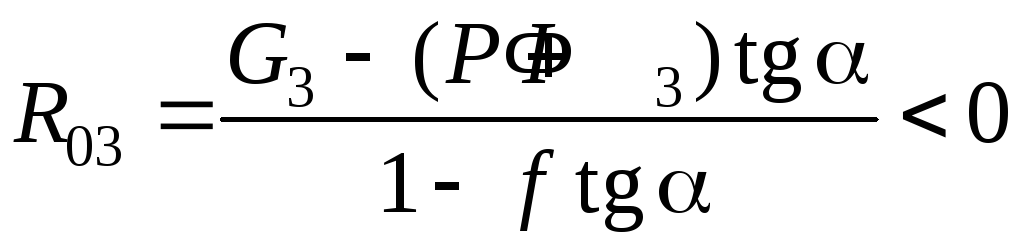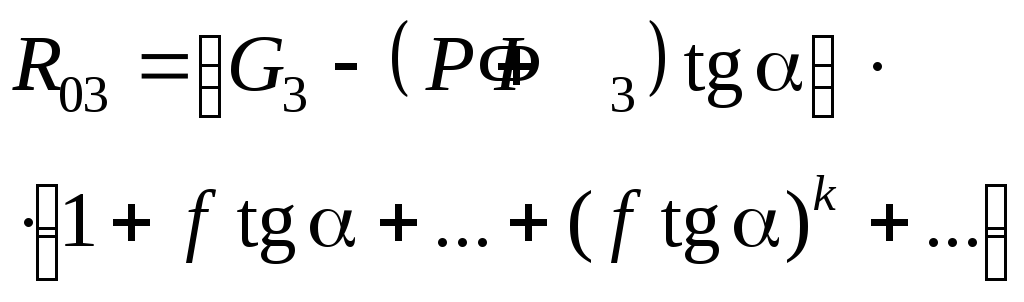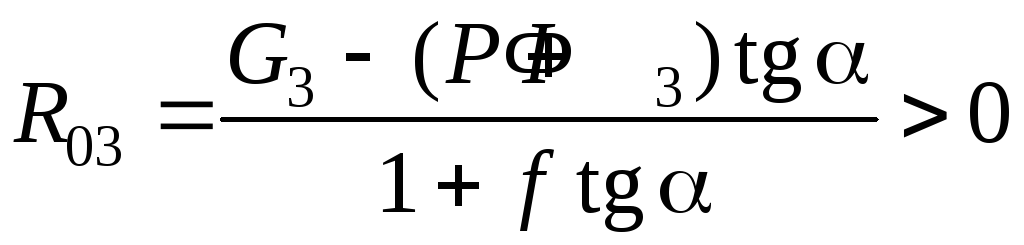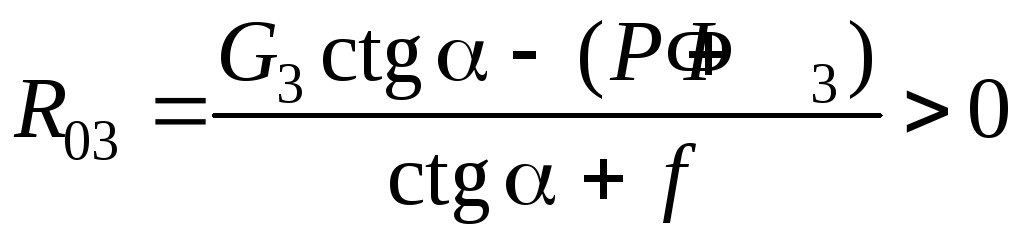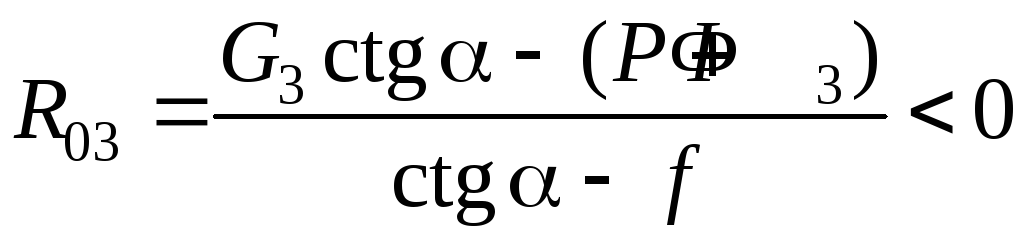Экзамен / тмм - экзамен(и задачи) / ТММ Экзамен! / Лекции / часть2 / tmm_13

5.3. Силовой расчет механизмов с трением

Рассмотрим два метода силового расчета с трением.

Первый метод (метод последовательных приближений). В первом приближении связи считают идеальными, силами трения пренебрегают. По найденным реакциям находят силы трения и повторяют силовой расчет, считая силы трения известными. Если силы реакции, найденные во втором приближении, незначительно (10-20 %) отличаются от сил реакций, найденных в первом приближении, то силовой расчет на этом заканчивается. Если требуется большая точность, то вычисляют следующие приближения до тех пор, пока разница между значениями сил реакций, найденных в последующем и предыдущем приближениях, не окажется меньше допустимого значения.

В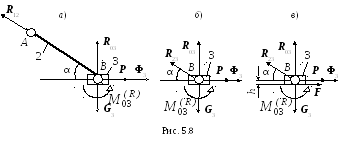 качестве примера рассмотрим кривошипно-ползунный механизм, изображенный на рис.4.4. Будем считать массу шатуна 2 пренебрежимо малой (рис.5.8, а); тогда силы реакций, приложенные к этому звену в шарнирах А и В, и , должны быть направлены по линии АВ. Отметим, что при сделанном допущении ползун 3 становится статически определимым.

Первое приближение. Полагая силы трения равными нулю, запишем уравнения кинетостатики для ползуна 3 (рис.5.8, б):

(5.17)

Здесь α – угол наклона звена 2 (и силы реакции ) к линии перемещения ползуна. Отсюда найдем силы реакции в первом приближении:

(5.18)

Приняв, что сила реакции в поступательной паре , найдем силу трения F, действующую на ползун со стороны стойки:

, (5.19)

где f – коэффициент трения в поступательной паре. Отметим, что, если , то контакт ползуна и стойки осуществляется по нижней плоскости, и сила трения F приложена так, как показано на рис.5.8, в. Если , то контакт ползуна и стойки происходит по верхней плоскости, и там же действует сила трения F. Направлена сила трения в любом случае против относительной скорости движения ползуна.

Второе приближение. Составим уравнения кинетостатики для ползуна, полагая, что сила трения F, действующая на ползун со стороны стойки, известна и равна (5.19), высота ползуна равна 2h – см. рис.5.8, в, а сила реакции > 0 (направлена вверх).

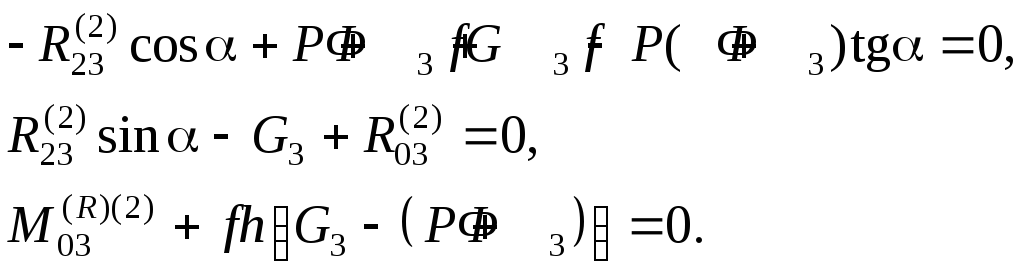(5.20)

Отсюда найдем силы реакции во втором приближении:

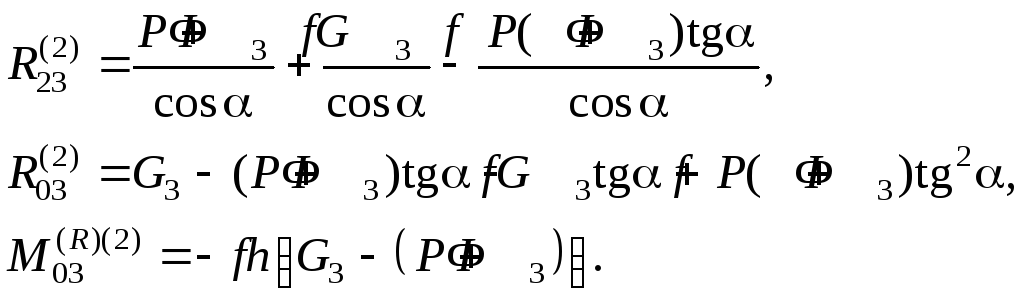(5.21)

Из сравнения выражений (5.21) и (5.18) видно, что значения всех сил реакций изменились:

а момент стал ненулевым.

Полагая, что , можно найти силу трения и, считая ее известной, найти следующее, третье приближение, и т.д.

Если сила реакции , т.е. направлена вниз, то второе приближение даст следующий результат:

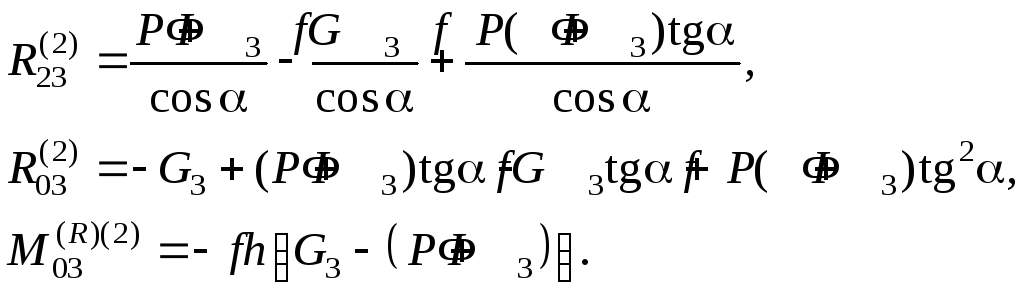(5.22)

Сравнивая (5.22) с (5.18), получим:

.

(к+1)-е приближение. Можно показать, что нормальная сила реакции , найденная в (к+1)-м приближении, в случае, когда G₃ – (P + Ф₃)tgα > 0, определяется по выражению:

. (5.23)

Из анализа соотношения (5.23) следует, что при f tgα < 1 разница между силой реакции , найденной в к-м и (к+1)-м приближениях, уменьшается с ростом к. Это соответствует случаю «малого» угла давления α и «малого» коэффициента трения f. При f tgα > 1 разница между силой реакции , найденной в к-м и (к+1)-м приближениях, с ростом к увеличивается, а сила реакции R₀₃ на каждом приближении меняет знак. При f tgα = 1 сила реакции , найденной в каждом последующем приближении, равна попеременно то 0, то .Это означает, что данный метод при условии f tgα 1 неприменим. Схема, соответствующая этому условию, приведена на рис.5.9.

Если G₃ – (P + Ф₃)tgα < 0, т.е. < 0 (направлена вниз), то несложно получить выражение:

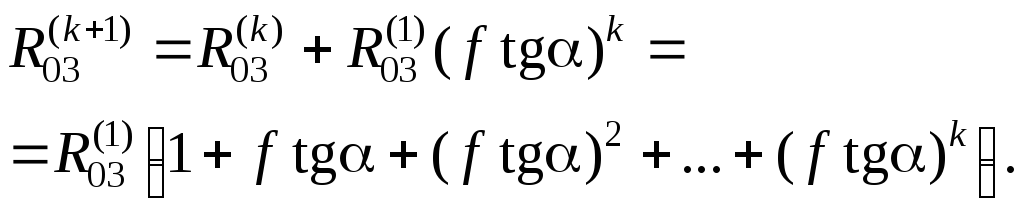(5.24)

Из соотношения (5.24) следует, что силу реакции и в этом случае можно найти только тогда, когда ftgα < 1; в противном случае (как на рис.5.9) метод последовательных приближений неприменим.

Второй метод. Силовой расчет сводится к совместному решению уравнений кинетостатики, содержащих силы трения в качестве дополнительных неизвестных, и полученных выше соотношений, являющихся математическими моделями кинематических пар с трением (см. п.5.2). При отсутствии избыточных связей число неизвестных оказывается при этом равным числу уравнений. Нетрудно, однако, заметить, что уравнения математических моделей кинематических пар с трением содержат нелинейные функции от входящих в них компонент реакций (модуль, знак реакции и т.п.); поэтому и полная система уравнений силового анализа оказывается нелинейной.

Нелинейность уравнений вызывает ряд существенных осложнений при их решении. Во-первых, процесс определения решения становится более трудоемким; как будет показано ниже, в ряде случаев приходится многократно решать системы линейных уравнений. Во-вторых, может обнаружиться, что в рассматриваемом положении механизма при заданных кинематических параметрах движения и заданных коэффициентах трения система уравнений силового расчета вообще не имеет решения. С физической точки зрения это означает, что исследуемое движение для данного механизма с трением оказывается невозможным ни при каких значениях движущих сил. В этом случае обычно говорят о заклинивании механизма. Частным случаем заклинивания является эффект самоторможения: механизм невозможно вывести из состояния покоя, какую бы силу ни прикладывать к его входному звену. Увеличение движущей силы вызывает в таком механизме увеличение сил трения, уравновешивающих ее действие. В-третьих, система нелинейных уравнений может иметь и несколько решений; иными словами, при одних и тех же активных силах механизм может совершать заданное движение при различных движущих силах и различных значениях реакций. Обычно это происходит в таких положениях механизма, в которых возможно самоторможение, но активные силы и силы инерции имеют положительную мощность, т.е. «помогают» движущей силе, вызывая эффект «оттормаживания». Выяснить, какое из решений будет соответствовать действительным значения реакций и движущих сил, не удается, если оставаться в рамках исходной динамической модели жесткого механизма.

Рассмотрим несколько примеров.

Расчет плоского рычажного механизма. Обратимся к тому же кривошипно-ползунному механизму, что и при рассмотрении первого метода (см. рис.4.4.). Как и ранее, будем считать массу шатуна 2 пренебрежимо малой, тогда силы реакций, приложенные к этому звену в шарнирах А и В, и , должны быть направлены по линии АВ. Зная направление силы , можно составить независимую систему уравнений кинетостатики для ползуна 3. Полагая, что ползун движется влево, т.е. < 0 и и используя модель поступательной пары с трением, описываемую уравнением (5.10), получаем следующую систему уравнений кинетостатики для ползуна (рис.5.10):

–R₂₃cosα + (P + Ф₃) + fR₀₃signR₀₃ = 0,

R₂₃sinα + R₀₃ – G₃ = 0, (5.25)

–R₀₃a + fR₀₃h = 0.

Здесь а – расстояние от оси шарнира В до линии действия силы реакции , fR₀₃signR₀₃ =F – сила трения. В системе уравнений (5.25) три неизвестных: R₂₃, R₀₃, a. Из третьего уравнения (5.25) находим: a = fh. Из второго уравнения (5.25) выразим R₂₃: . Подставляя R₂₃ в первое уравнение (5.25), получим R₀₃:

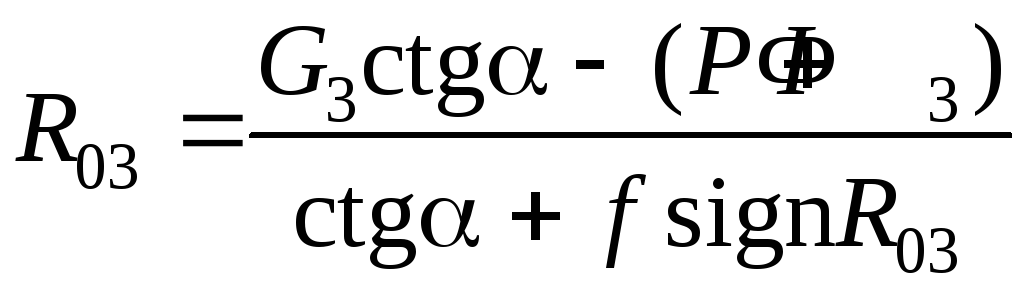(5.26)

Это уравнение – нелинейное, так как функция signR₀₃ – нелинейна. Найдем решение этого уравнения при различных соотношениях между α и f, а также G₃ и Р + Ф₃ . Рассмотрим четыре возможных варианта (табл. 5.3):

Таблица 5.3

	«малое» трение: f < ctgα	«большое» трение: f > ctgα
G3ctgα – (P + Ф3) < 0	Вариант 1.1.	Вариант 1.2.
G3ctgα – (P + Ф3) > 0	Вариант 2.1.	Вариант 2.2.

Вариант 1.1. «Малое» трение; рабочая нагрузка P и сила инерции Ф₃ направлены против скорости ползуна («препятствуют» движению ползуна). Возможно единственное решение при R₀₃ < 0 (sign R₀₃ = – 1):

.

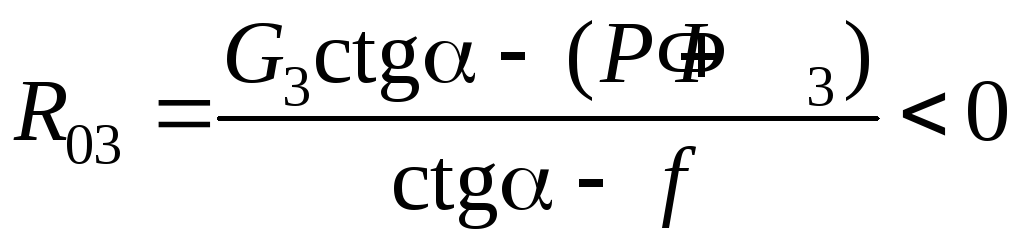Контакт ползуна и стойки происходит по верхней плоскости, сила реакции R₀₃ направлена сверху вниз, Это – обычный тяговый режим. Отметим, что вариант R₀₃ > 0 (sign R₀₃ = + 1) невозможен: числитель в дроби (5.26) отрицательный, знаменатель – положительный, следовательно, дробь отрицательна.

Вариант 2.1. «Малое» трение; силы P и Ф₃ направлены против оси х («помогают» движению ползуна). В дроби (5.26) числитель положительный, знаменатель – положительный, следовательно, дробь также положительна. Существует единственное решение при R₀₃ > 0 (sign R₀₃ = + 1):

.

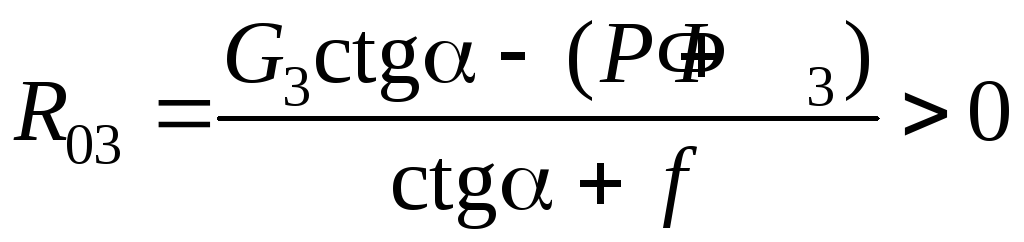Контакт ползуна и стойки происходит по нижней плоскости, сила реакции R₀₃ направлена снизу вверх. Движение ползуна происходит за счет действия рабочей нагрузки и силы инерции. Это – инверсный тяговый режим.

Вариант 1.2. «Большое» трение; рабочая нагрузка P и сила инерции Ф₃ направлены против скорости ползуна. Уравнение (5.26) не имеет решения. Действительно, положив R₀₃ > 0 (sign R₀₃ = + 1), получим ,

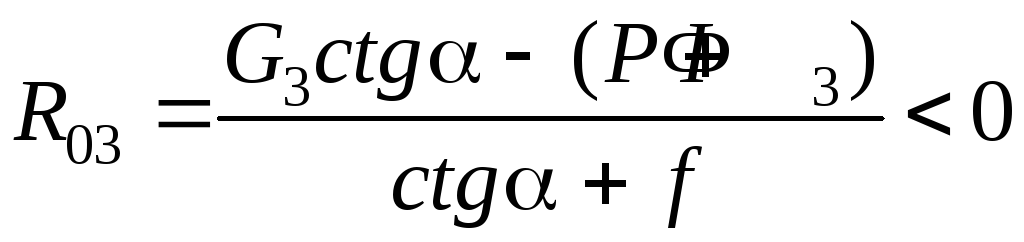т.к. числитель дроби отрицательный, а знаменатель – положительный. При R₀₃ < 0 (sign R₀₃ = – 1) имее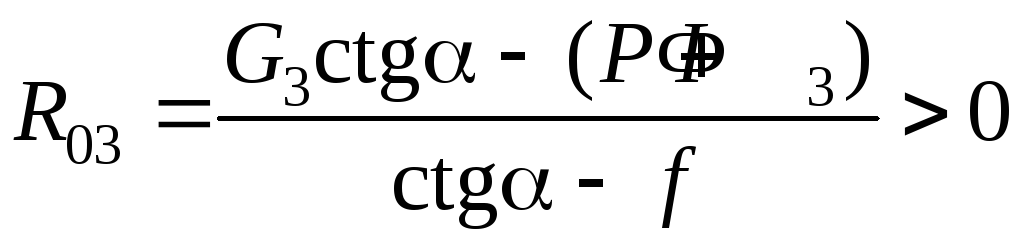м , поскольку числитель и знаменатель дроби отрицательные. Получающееся противоречие показывает, что решения не существует. Этот случай соответствует режиму самоторможения, при котором в рассматриваемом положении механизма и при заданном направлении силы движение вообще становится невозможным.

Вариант 2.2. «Большое» трение; силы P и Ф₃ направлены против оси х («помогают» движению ползуна). Тогда уравнение (5.26) имеет два решения. Действительно, полагая, что R₀₃ > 0 (sign R₀₃ = + 1), имеем:

,

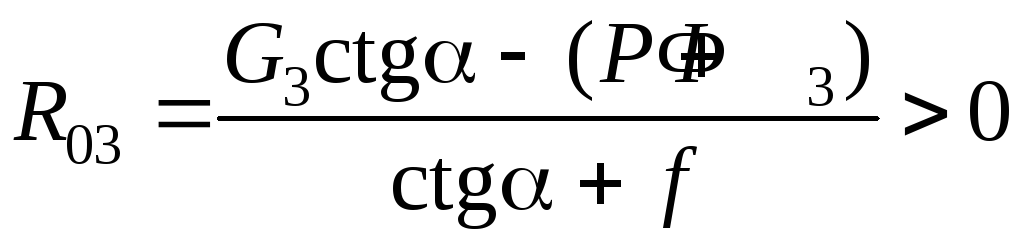поскольку числитель и знаменатель дроби положительные. Положив R₀₃ < 0 (sign R₀₃ = – 1), получаем второе решение 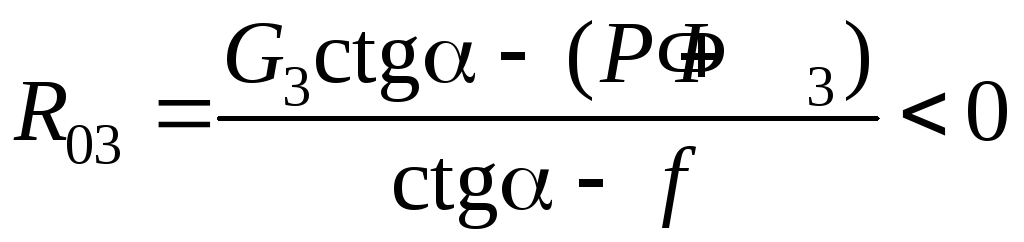, поскольку числитель положительный, а знаменатель отрицательный. В этом случае мы имеем дело с режимом оттормаживания: при «большом» трении движение возможно в том случае, когда вектор Р + Ф₃ направлен так же, как и скорость ползуна. Существование двух режимов оттормаживания является одним из парадоксов Кулонова трения, подробно исследованных в книге Пенлеве¹. Установить, какое из решений будет фактически осуществляться, строго говоря, в рамках модели механизма с жесткими звеньями невозможно. Можно только показать, что некоторые «физические» соображения свидетельствуют в пользу первого решения. Нетрудно понять, что при увеличении коэффициента трения f следует ожидать увеличения модуля силы трения |F| , т.е. должно быть d|F|/df>0. Исследуя первое решение, получаем

,

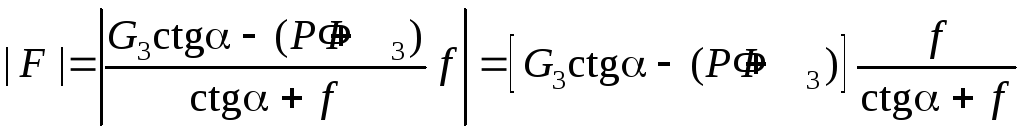поскольку G₃ctgα – (P + Ф₃) > 0. Следовательно,

.

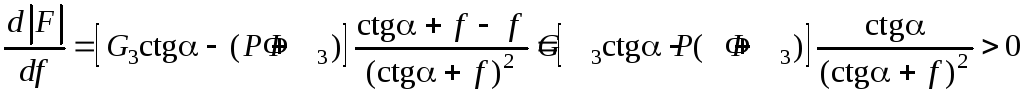Для второго решения находим

,

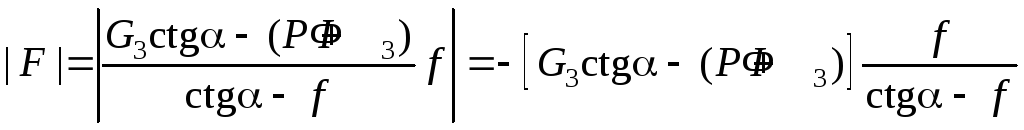поскольку ctgα – f < 0. Следовательно,

.

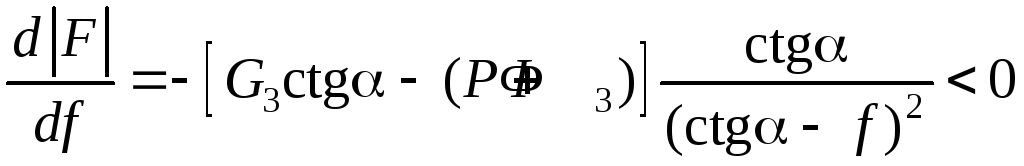Поэтому второе решение является с физической точки зрения «недостоверным».

Сведем все найденные решения в табл. 5.4. Для удобства сравнения результатов, полученных двумя методами, разделим числитель и знаменатель дроби выражения (5.26) на ctgα.

Таблица 5.4

	«Малое» трение: f < ctgα	«Большое» трение: f > ctgα
G3ctgα – (P + Ф3) < 0	Тяговый режим	Нет решения. Режим самоторможения
Метод последовательных приближений		–
G3ctgα – (P + Ф3) > 0	Инверсный тяговый режим	Режим оттормаживания
Метод последовательных приближений	ּ[+ +]	–

Определив силы реакций, действующие на ползун, легко найти остальные реакции, возникающие в механизме. Так, рассматривая равновесие звена 2, получаем (m₂  0): R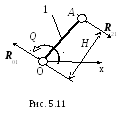₁₂ = R₂₃, а уравнения кинетостатики для звена 1 дают (рис. 5.11): , Q = R₁₂H, где H – расстояние от точки 0 до линии АВ.

Расчет плоского кулачкового механизма. Рассмотрим плоский кулачковый механизм с поступательно движущимся толкателем (рис.5.12). Ограничимся определением компонент реакций, действующих в плоскости движения. Уравнения кинетостатики, составленные для толкателя и кулачка, разделяются и могут решаться независимо. Составим уравнения кинетостатики для толкателя. Силы, действующие на толкатель со стороны кулачка, сводятся к силе , направленной по нормали к профилю кулачка в рассматриваемом положении, и силе трения . Выберем модель поступательной пары с двухточечным контактом; силы , и соответствующие силы трения и действуют на толкатель со стороны стойки. Введем систему координат 0₂x₂y₂, связанную с толкателем; в результате получаем уравнения кинетостатики в следующем виде:

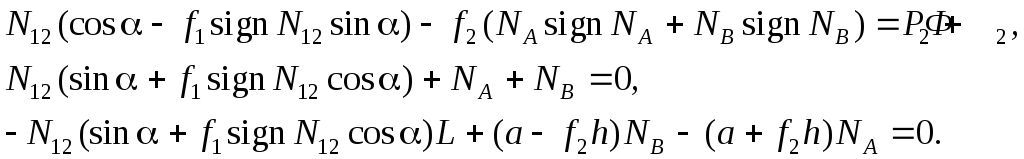(5.27)

Здесь α и f₁ – соответственно угол давления и коэффициент трения в высшей кинематической паре К, f₂ – коэффициент трения в поступательной паре, P₂ – рабочая нагрузка, Ф₂ – сила инерции толкателя, а, h, L – геометрические параметры, обозначенные на рисунке. Силы P₂ и Ф₂ считаются положительными, если они направлены так, как они показаны на рисунке.

Система уравнений (5.27) является нелинейной: в ней присутствуют функции signN₁₂, signN_A, signN_B, имеющие разрывы при N₁₂=0, N_A=0, N_B=0. Урав-нения станут линейными, если задать знаки неизвестных реакций. Предварительно выберем знаки N₁₂, N_A, N_B такими, какими они получились бы в рассматриваемом положении механизма, если бы силы трения отсутствовали. Полагая f₁=0, f₂=0, получаем:

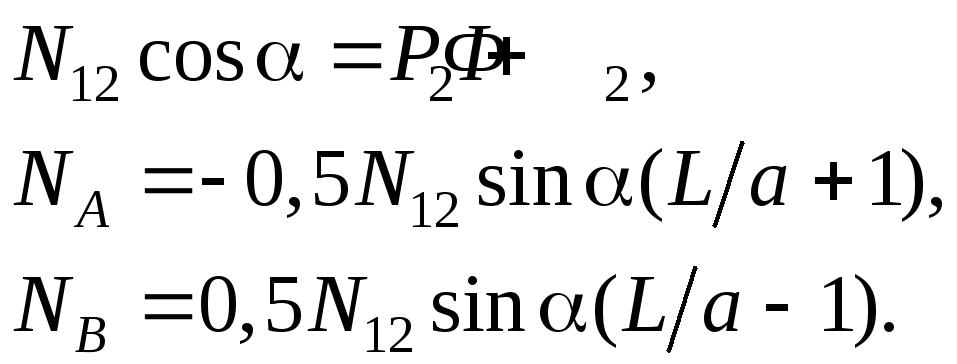
При заданном направлении сил P₂ и Ф₂ (эти силы прижимают толкатель к профилю кулачка) получаем N₁₂>0, N_A<0, N_B>0 (если L>a). Подставив в уравнения кинетостатики signN₁₂=1, signN_A=–1, signN_B=1, приходим к системе линейных уравнений

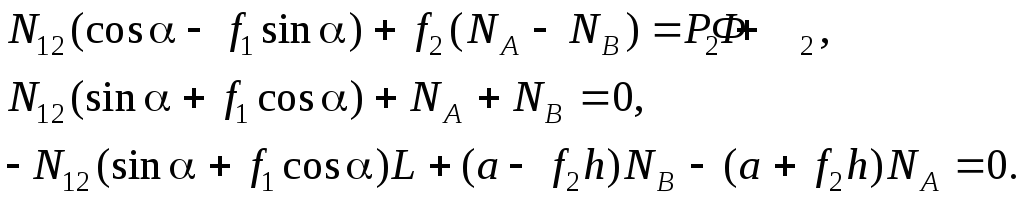(5.28)

Из последних двух уравнений находим N_A и N_B:

(5.29)

Если L > a + f₂h , то при N₁₂ > 0 будет действительно N_A < 0 и N_B > 0. Подставим N_A и N_B в первое уравнение (5.28) и найдем из него реакцию N₁₂:

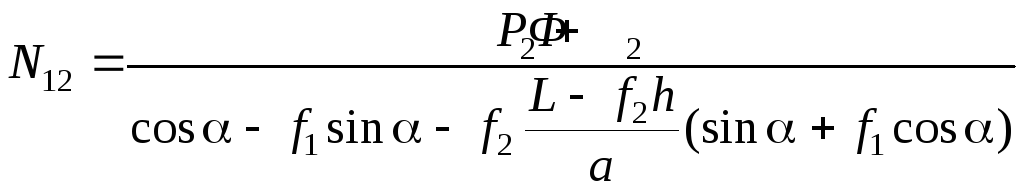. (5.30)

Если Р₂ + Ф₂ > 0, то реакция N₁₂ останется положительной в системе с трением при выполнении условия

. (5.31)

При увеличении угла давления α или коэффициентов трения f₁ и f₂ значение σ уменьшается; при cosα = f₁sinα, т.е. при ctgα = f₁ она наверняка становится отрицательной. С уменьшением σ увеличивается значение |N₁₂|, при σ = 0 реакция становится «бесконечно большой», что свидетельствует о заклинивании механизма. Значения σ, при которых N₁₂ < 0, вообще не должны рассматриваться, поскольку такое решение не удовлетворяет тем условиям, при которых были получены уравнения (5.28). Могут ли исходные уравнения (5.27) иметь решение, в котором N₁₂ < 0 при Р₂ + Ф₂ > 0 ? Если при этом принять, что N_A>0, N_B<0, то из (5.27) получаем

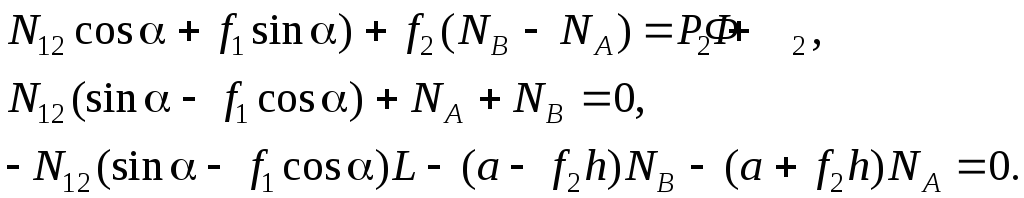(5.32)

Из последних двух уравнений находим:

(5.33)

Полагая, что N₁₂ < 0, sinα > f₁cosα (сtgα < f₁), получаем, действительно, N_A > 0, N_B < 0. Подставив (5.33) в первое уравнение (5.32), имеем:

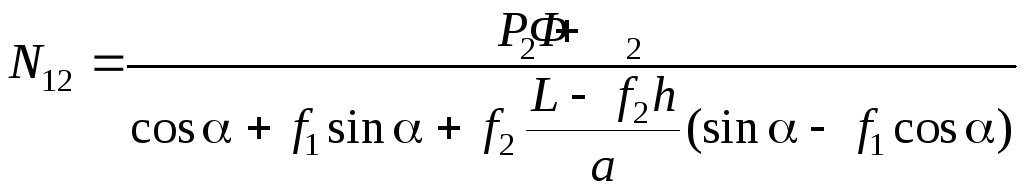. (5.34)

Это уравнение, а следовательно, и исходная система не может иметь решение N₁₂ < 0 при Р₂ + Ф₂ > 0, какими бы ни были значения α и f₂. Таким образом, при σ < 0 исходная система уравнений вообще не имеет решений, если Р₂+Ф₂>0.

Пусть Р₂ + Ф₂ < 0, т.е. предположим, что направление суммарной силы совпадает с направлением скорости толкателя . Может ли система уравнений (5.27) иметь при этом решение, в котором N₁₂ > 0, N_A < 0, N_B > 0? Если L > a + f₂h, то для определения N₁₂ вновь получаем выражение (5.30), из которого следует, что при σ < 0 и Р₂ + Ф₂ < 0 будем иметь N₁₂ > 0, а тогда в силу соотношений (5.29) имеем N_A < 0, N_B > 0.

Таким образом, при выполнении условия σ < 0 движение возможно, если сумма рабочей нагрузки и силы инерции направлена по скорости, т.е. играет роль движущей силы. Это – режим оттормаживания, о котором уже говорилось ранее.

Возможно и другое решение, в котором N₁₂ < 0, N_A > 0, N_B < 0. Действительно, при таких знаках реакций мы приходим к уравнениям (5.32), а затем – к выражению (5.34), из которого при Р₂ + Ф₂ < 0 и при ctgα > f₁ получается второе решение N₁₂ < 0, поскольку выражение, стоящее в знаменателе, в этом случае положительно.

Существование двух режимов оттормаживания легко объяснить: в первом режиме (N₁₂ > 0) сила N₁₂, складываясь с приложенными силами, преодолевает вместе с ними силы трения; во втором режиме (N₁₂ < 0) сила N₁₂, складываясь с силами трения, препятствует движению толкателя. Установить, какой из этих двух режимов будет происходить в реальной системе, невозможно. Впрочем, в реальных кулачковых механизмах обычно максимальные углы давления выбираются с таким расчетом, чтобы условие ctgα < f₁ не выполнялось во избежание возможности заклинивания; тем самым и режим оттормаживания не реализуется.

Определив реакции в высшей кинематической паре (силы N₁₂ и F₁₂), можно перейти к силовому расчету кулачка. Составляя уравнения кинетостатики в системе осей 0₁х₁y₁ и используя соотношение (5.14), получаем (полагая, что , а центр кулачка совпадает с точкой 0₁):

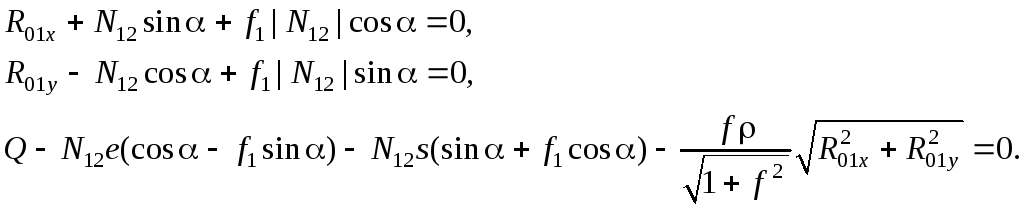(5.35)

где е – эксцентриситет кулачкового механизма, s – координата толкателя, f – коэффициент трения во вращательной паре, ρ – радиус цапфы вала кулачка. Из уравнений (5.35) можно определить реакции во вращательной паре и движущий момент Q.

Силовой расчет червячной передачи (рис. 5.13). Червячная передача содержит одну высшую пятиподвижную кинематическую пару, динамическая модель которой представляется уравнениями (5.16), и две вращательные пары. Пренебрежем трением во вращательных парах, поскольку оно обычно оказывается значительно менее существенным, чем трение в червячном зацеплении. Уравнения кинетостатики для червячного колеса и червяка оказываются независимыми. Сначала составим уравнения кинетостатики для червячного колеса. Положим, что оси координат 0₂xyz являются главными центральными осями инерции колеса. Используем соотношения (5.16). Обозначим: r₂ – начальный радиус червячного колеса, J₂₀ – момент инерции колеса относительно оси 0₂z (точка 0₂z совпадает с центром масс колеса). Проецируя силы, действующие на колесо, на оси координат 0₂xyz и составляя уравнения моментов относительно этих осей, получаем систему шести уравнений с шестью неизвестными (N_Ax, N_ay, N_Cx, N_Cy, N_2z, N₁₂):

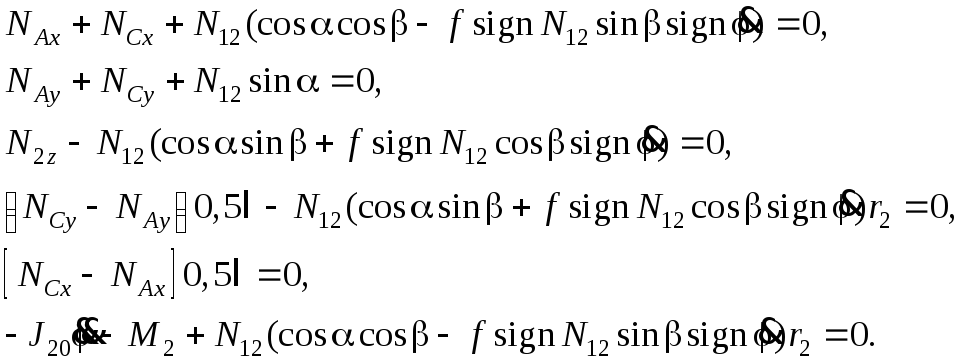(5.36)

Пусть направление угловой скорости совпадает с показанным на рисунке: > 0 (sign = +1). Из последнего уравнения (5.36) определим N₁₂: