КР1 / кр1

Содержание контрольной работы №1

1. Векторная алгебра.

2. Прямая на плоскости.

3. Прямая и плоскость в пространстве.

4. Прямая и плоскость в пространстве.

Вариант 0

1. Найдите объём тетраэдра с вершинами в точках А(–1, –5, 2), B(–6, 0, –3), C(3, –6, –3),

D(–10, 6, 7) и длину его высоты, опущенной из вершины D.

2. О(0, 0) – точка пересечения высот треугольника ABC, –

уравнения его сторон. Составьте уравнение третьей стороны.

3. Найдите проекцию точки на прямую .

4. Найдите расстояние от точки М(1, 1, 1) до прямой .

Решение варианта 0

1. Найдите объём тетраэдра с вершинами в точках А(–1, –5, 2), B(–6, 0, –3), C(3, –6, –3),

D(–10, 6, 7) и длину его высоты, опущенной из вершины D.

►

Рис. 1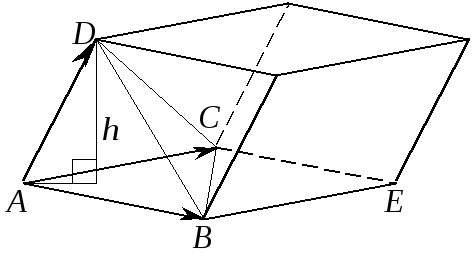

Рассмотрим векторы: , . Они служат рёбрами тетраэдра ABCD и одновременно рёбрами параллелепипеда с основанием ABEC (см. рис. 1). Очевидно, тетраэдр и параллелепипед имеют одну и ту же высоту h, при этом объём тетраэдра составляет одну шестую часть объёма параллелепипеда . Действительно, .

Так как , то . Вычислим :

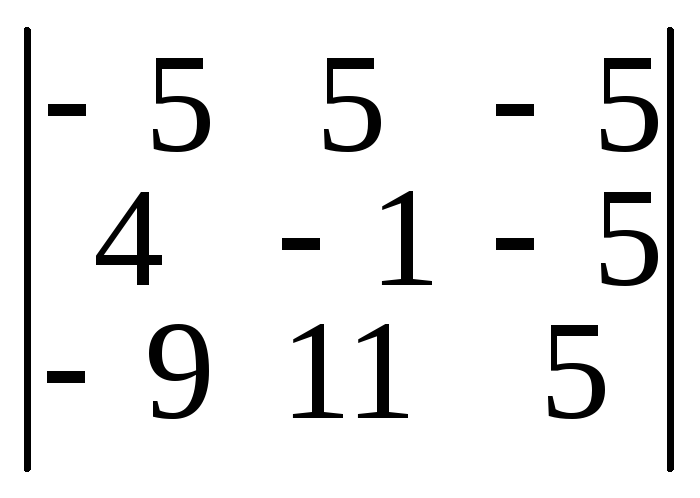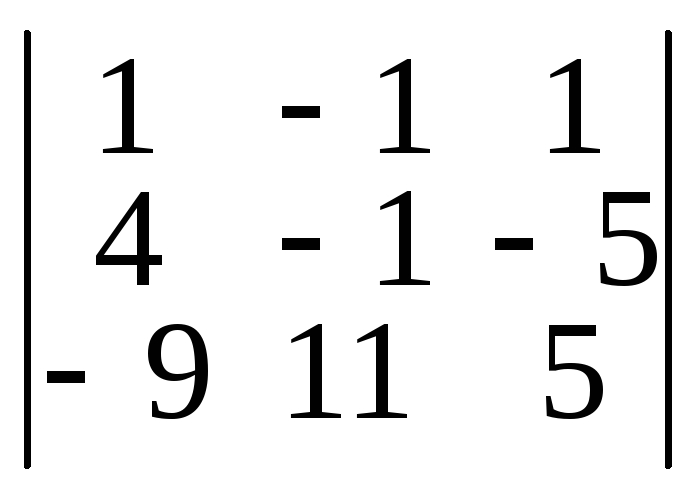= = –5 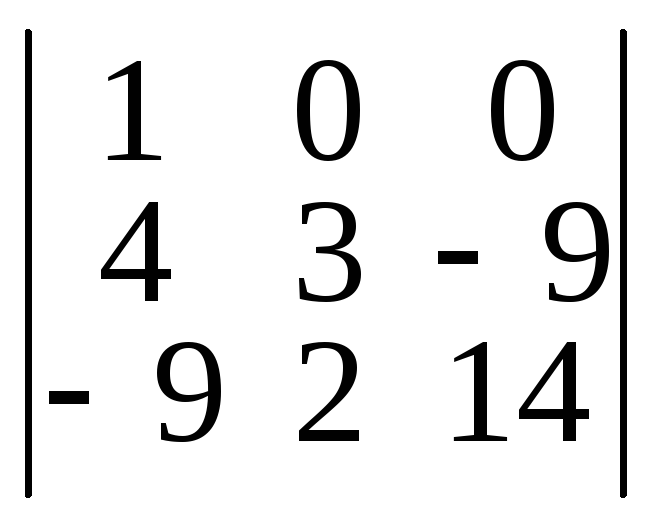= –5 = –5=

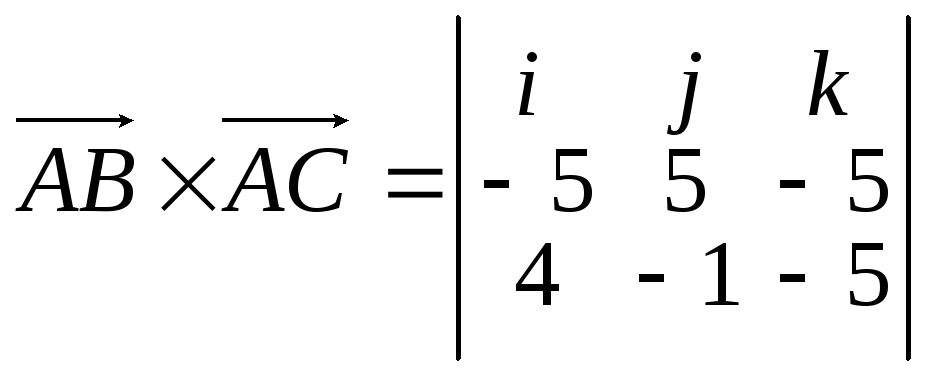
= –5(3∙14 – 2∙(–9)) = –300 и, следовательно, |–300| = 50. Поскольку , = то .◄

2. О(0, 0) – точка пересечения высот треугольника ABC, –

уравнения его сторон. Составить уравнение третьей стороны.

►Положим AB: BC:, а из вершин треугольника А и С опустим высоты AM и CN на эти стороны (рис. 2). Векторы нормали и к этим

Рис. 2. К примеру 3

сторонам, очевидно, могут служить направляющими векторами и для построенных высот. Стороны AB и ВС заданы общими уравнениями, коэффициенты при х и у в которых трактуются как координаты векторов нормалей, поэтому =(1, 3), =(3, 5). Теперь можно написать канонические уравнения данных высот, т.е. уравнения вида:

, (2)

где – координаты любой точки , принадлежащей прямой, а – координаты любого вектора , параллельного этой прямой и называемого её направляющим вектором. Подставив в (2) вместо координаты точки О(0, 0), а вместо – координаты векторов и , получим: CN: , AM: или CN: у = 3х, AM: . Решив совместно уравнения AB и AM, ВС и CN, получаем координаты точек А и С: . Уравнение стороны АС получим, подставив координаты точек А и С в уравнение прямой, проходящей через две данные точки:

. (3)

Имеем или 39х – 9у – 4 = 0. Ответ: 39х – 9у – 4 = 0.◄

3. Найти проекцию точки на прямую .

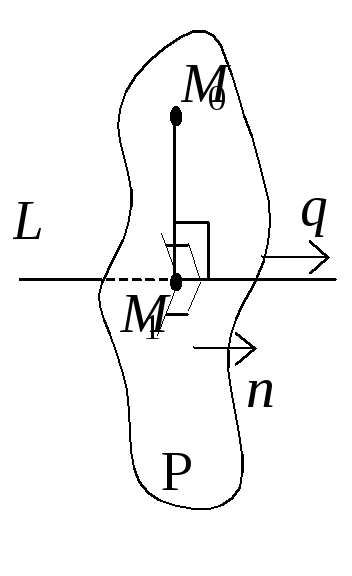
Рис. 3. К примеру 3.

►Проекцией точки М₀ на прямую L является основание перпендикуляра, опущенного из этой точки на данную прямую (рис. 3, точка М₁ –проекция точки М₀ на прямую L). Сначала напишем уравнение плоскости P, проходящей через точку М₀ перпендикулярно данной прямой. Зададим P как одну из плоскостей связки с центром в точке :

, (1)

где А, В, С – координаты вектора нормали к плоскости P, которые можно определить с точностью до постоянного множителя, так как при умножении обеих частей этого уравнения на одно и тоже число получаем уравнение, равносильное данному и поэтому задающее ту же плоскость. Вектор нормали к плоскости P здесь можно считать равным направляющему вектору прямой L из условия задачи (см. рис. 1). Подставив его координаты в (1), после очевидных преобразований получаем уравнение плоскости P : . Координаты точки М₁ найдём как точки пересечения этой плоскости с прямой L (рис. 1). Для этого надо решить систему из уравнений прямой L и уравнения плоскости P, при этом удобно использовать параметрические уравнения L. Чтобы получить их из канонических уравнений L, равные отношения в последних приравняем к t: . Из этих равенств выразим x, y, z: Получаем следующую систему уравнений: Подставим три последних уравнения системы в её первое уравнение: , получим или . Найденное значение t подставим в каждое из трёх последних уравнений системы: . Таким образом, имеем . Ответ: ◄

4. Найдите расстояние от точки М(1, 1, 1) до прямой .

Рис. 4. К примеру 4.

►Расстояние от точки M до прямой L найдём средствами векторной алгебры как высоту параллелограмма, изображённого на рис. 4. Площадь этого параллелограма есть модуль вектор-ного произведения: , где М₀(‒3, 1, 2) ‒ точка, принадлежащая прямой L, М(1, 1, 1) ‒ данная точка, ‒ направляющий вектор прямой L. Длина основания параллелограмма есть . Поэтому . . , =,

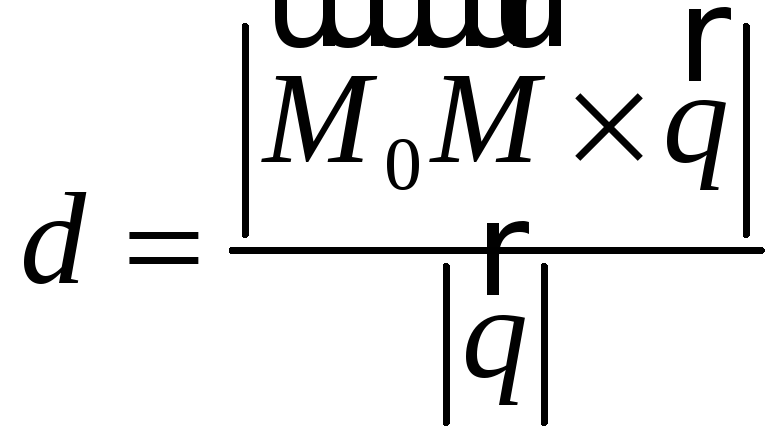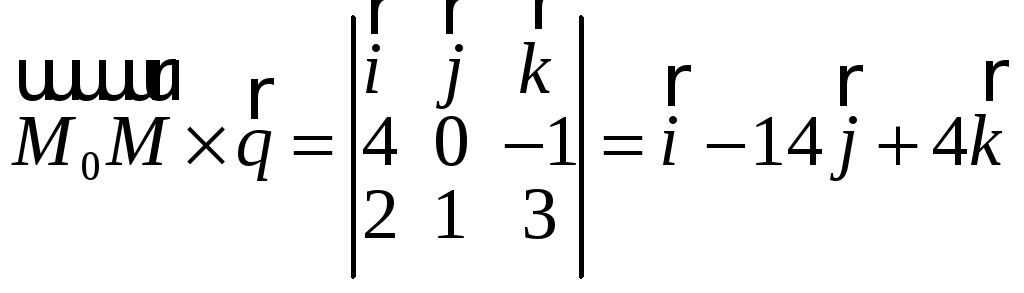Ответ: ◄

3