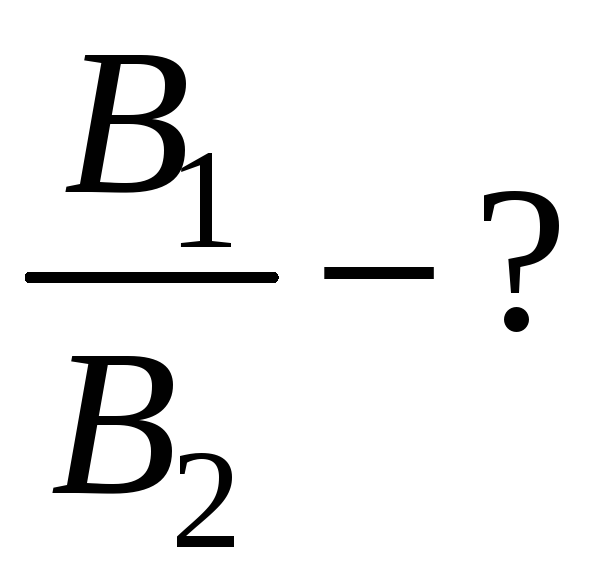Контрольная работа № 2
Вариант 4
Задачи 204, 214, 224, 234, 244, 254, 264, 254, 284, 294
Задача 204
ЭДС батареи 80 В, внутреннее сопротивление 5 Ом. Внешняя цепь потребляет мощность 100 Вт. Найти силу тока в цепи, ее сопротивление и напряжение, под которым находится внешняя цепь
Дано:
|
|
|
|
Мощность, выделяющаяся во внешней цепи, определяется по формуле [2, с.238]
![]() . (1)
. (1)
Согласно закону Ома для замкнутой цепи [2, с.238]
![]() . (2)
. (2)
Подставляя (2) в (1), получим
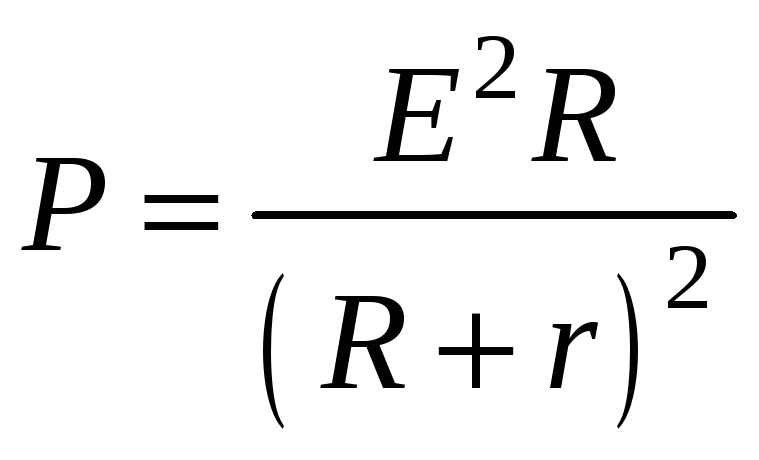 . (3)
. (3)
Решаем полученное уравнение относительно
внешнего сопротивления цепи
![]() .
Тогда последовательно будем иметь
.
Тогда последовательно будем иметь
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Получили квадратное уравнение относительно
переменной
![]() .
Решаем его, предварительно подставив
известные числовые значения величин.
Тогда получим
.
Решаем его, предварительно подставив
известные числовые значения величин.
Тогда получим
![]() ;
;
![]() ;
;
![]() .
.
Решением данного уравнения являются
значения
![]() Ом и
Ом и
![]() Ом.
Ом.
а)
![]() Ом.
Ом.
Мощность можно определить также по формуле
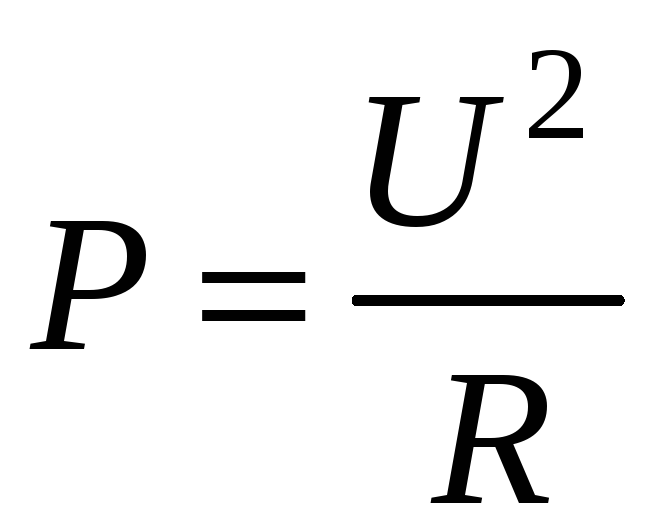 ,
,
откуда находим напряжение на внешнем сопротивлении
![]() В.
В.
Сила тока в цепи
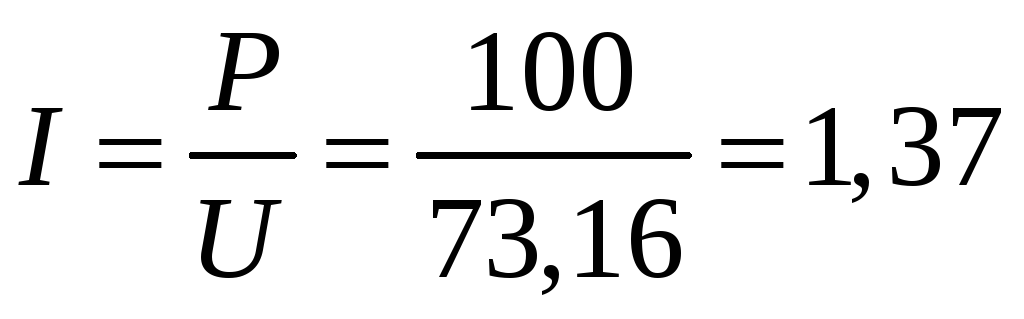 А.
А.
а)
![]() Ом.
Ом.
Напряжение на внешнем сопротивлении
![]() В.
В.
Сила тока в цепи
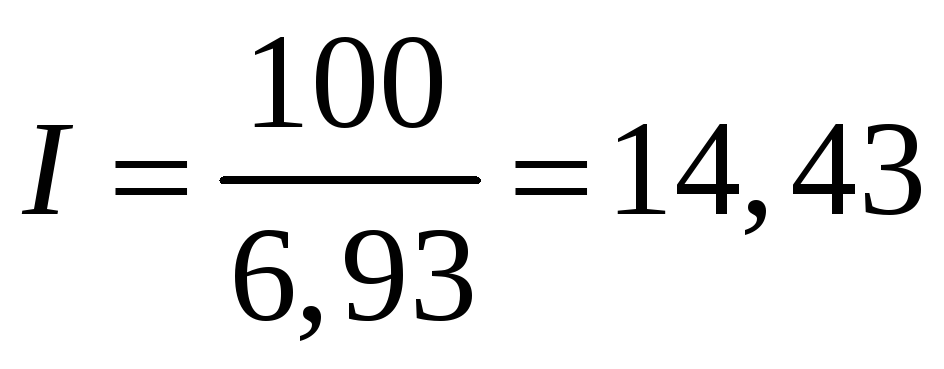 А.
А.
Ответ: а)
![]() Ом;
Ом;
![]() В;
В;
![]() А;
А;
б)
![]() Ом;
Ом;
![]() В;
В;
![]() А.
А.
Задача 214
По тонкому проводнику в виде дуги радиусом R течет ток I. Найти индукцию магнитного поля в точке О в случае, указанному на рис.26,а.

Дано:
|
|
|
|
Магнитную индукцию поля
![]() в точке О можно найти, используя выражение
для магнитной индукции в центре кругового
проводника с током
в точке О можно найти, используя выражение
для магнитной индукции в центре кругового
проводника с током
![]() [2, с.256]:
[2, с.256]:
![]() ,
,
где ![]() Гн/м
– магнитная постоянная;
Гн/м
– магнитная постоянная;
![]() – магнитная проницаемость среды.
– магнитная проницаемость среды.
Учитывая равный вклад в магнитную индукцию каждой элементарной части проводника, будем иметь:
длина окружности радиуса
![]()
![]() ;
;
длина дуги радиуса
![]() и центрального угла
и центрального угла
![]() (рад)
(рад)
![]() .
.
Тогда искомая магнитная индукция будет равна
![]() .
.
Таким образом,
![]() .
.
Ответ:
![]() .
.
Задача 224
Постоянный ток I течет по проводу, намотанному на деревянный то-роид малого поперечного сечения. Число витков N. Найти отношение индукции магнитного поля внутри тороида к индукции в центре тороида.
Дано:
|
|
|
|
Индукцию на оси внутри тороида найдем с помощью теоремы о циркуляции вектора магнитной индукции [2, с.287]
![]()
где ![]() Гн/м
– магнитная постоянная;
Гн/м
– магнитная постоянная;
![]() – алгебраическая сумма токов, охватываемых
контуром;
– алгебраическая сумма токов, охватываемых
контуром;
![]() – число токов.
– число токов.
Введем обозначение
![]() – радиус оси тороида. Тогда будем иметь
– радиус оси тороида. Тогда будем иметь
![]() ,
,
откуда находим
![]() . (1)
. (1)
Так как ток входит в тороид и выходит
из него практически из одной точки, то
ток
![]() протекает также вдоль оси тороида,
являясь кольцевым током. Для кольцевого
тока имеем [2, с.256]
протекает также вдоль оси тороида,
являясь кольцевым током. Для кольцевого
тока имеем [2, с.256]
![]() . (2)
. (2)
Используя формулы (1) и (2), находим искомое отношение
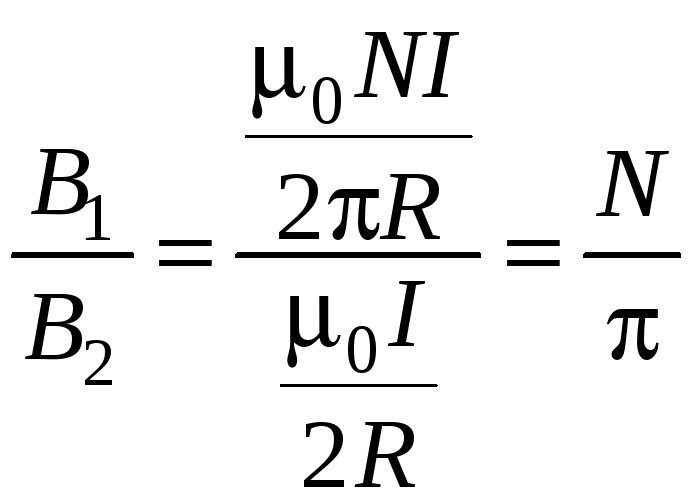 .
.
Ответ:
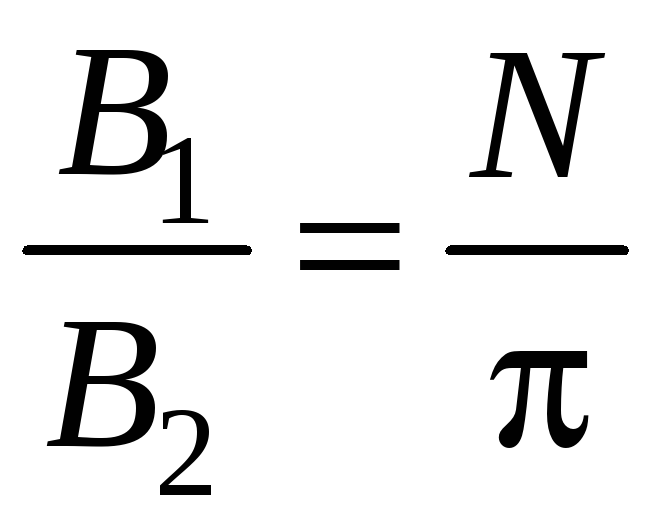 .
.
Задача 234
Проводник 1–2 массой m скользит без
трения по двум длинным проводящим
рельсам, расположенным на расстоянии
l друг от друга (рис.33). На левом конце
рельсы замкнуты сопротивлением R.
Система находится в вертикальном
однородном магнитном поле с индукцией
B. В момент
![]() стержню 1–2 сообщили вправо начальную
скорость
стержню 1–2 сообщили вправо начальную
скорость
![]() .
Пренебрегая сопротивлением рельсов и
стержня 1–2, а также самоиндукцией,
найти:
.
Пренебрегая сопротивлением рельсов и
стержня 1–2, а также самоиндукцией,
найти:
а) расстояние, пройденное стержнем до остановки;
б) количество тепла, выделенное при этом на сопротивлении.
Дано:
|
|
|
|
Проводник, рельсы и сопротивление
образуют замкнутый контур. Площадь
этого контура изменяется, поэтому в нем
возникает индукционный ток. Тогда на
проводник будет действовать сила Ампера,
модуль которой в данный момент времени
![]() будет равен
будет равен
![]() . (1)
. (1)
Согласно закону Ома, сила индукционного тока будет равна
![]() , (2)
, (2)
где ![]() – ЭДС индукции.
– ЭДС индукции.
По закону электромагнитной индукции
 , (3)
, (3)
где ![]() – изменение магнитного потока за время
– изменение магнитного потока за время
![]() .
.
Магнитная индукция в данной задаче постоянна, поэтому
![]() , (4)
, (4)
где ![]() – изменение площади, ограниченной
контуром за время
– изменение площади, ограниченной
контуром за время
![]() .
.
Пусть
![]() – скорость перемещения проводника.
Тогда
– скорость перемещения проводника.
Тогда
![]() . (5)
. (5)
Подставляя (5) в (4), а затем (4) в (3), последовательно получим
![]() ;
;
 ;
;
![]() . (6)
. (6)
Далее, используя выражения (2) и (1), получаем
![]() ;
;
 . (7)
. (7)
Согласно второму закону Ньютона с учетом замедленного движения проводника будем иметь
 .
.
Поскольку ускорение
![]() ,
то получаем следующее дифференциальное
уравнение
,
то получаем следующее дифференциальное
уравнение
 .
.
Разделяя в нем переменные, будем иметь
 . (8)
. (8)
Интегрируя уравнение (8), находим
 ;
;
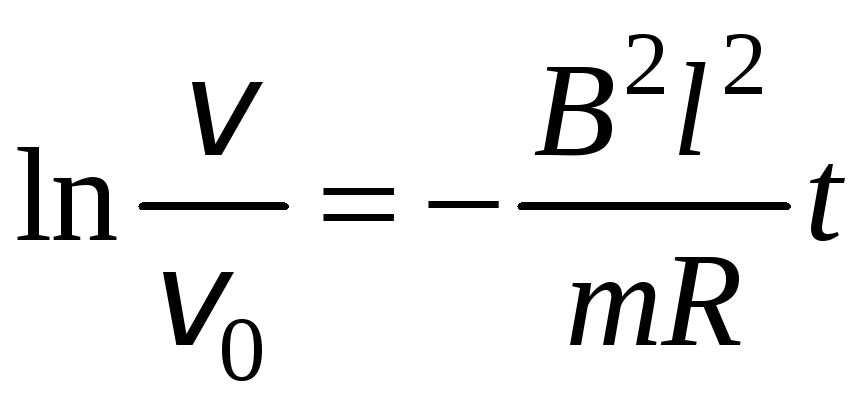 ,
,
откуда скорость проводника будет равна
![]() . (9)
. (9)
Поскольку скорость
![]() ,
то получаем следующее дифференциальное
уравнение
,
то получаем следующее дифференциальное
уравнение
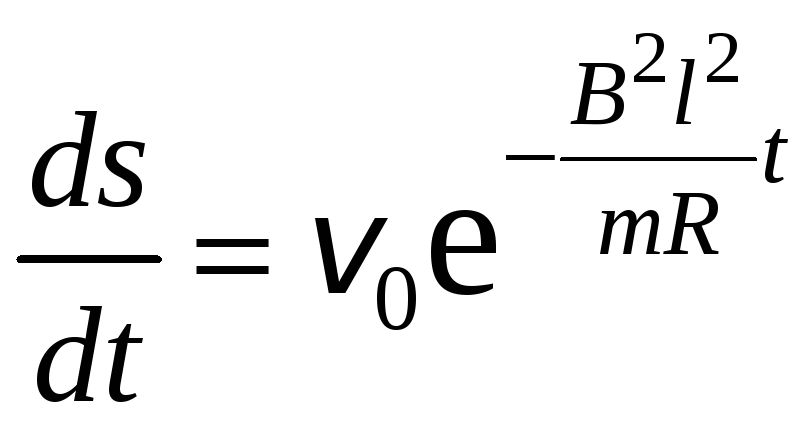
или
![]() .
.
Интегрируя последнее уравнение в
пределах от
![]() до
до
![]() (гарантированной остановки проводника),
получим
(гарантированной остановки проводника),
получим
 .
.
Таким образом,
![]() . (10)
. (10)
Количество тепла, выделенное при перемещении проводника, будет равно (так как сила тока величина переменная, то непосредственно использовать закон Джоуля–Ленца нельзя)
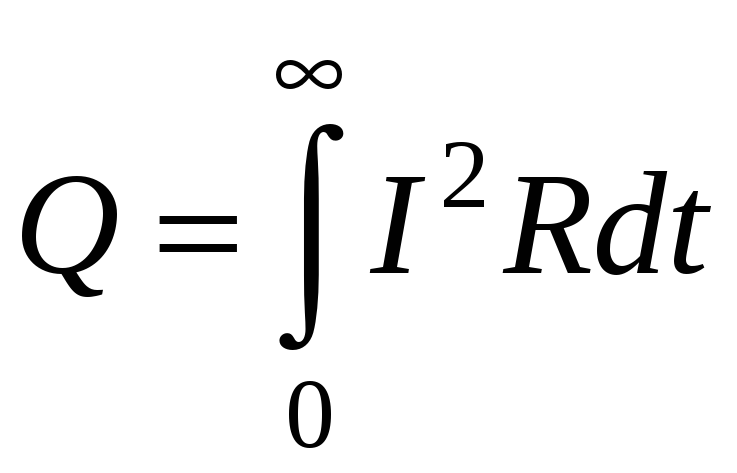 . (11)
. (11)
Используя формулу
![]() и выражение (9), получим
и выражение (9), получим
 .
.
Таким образом,
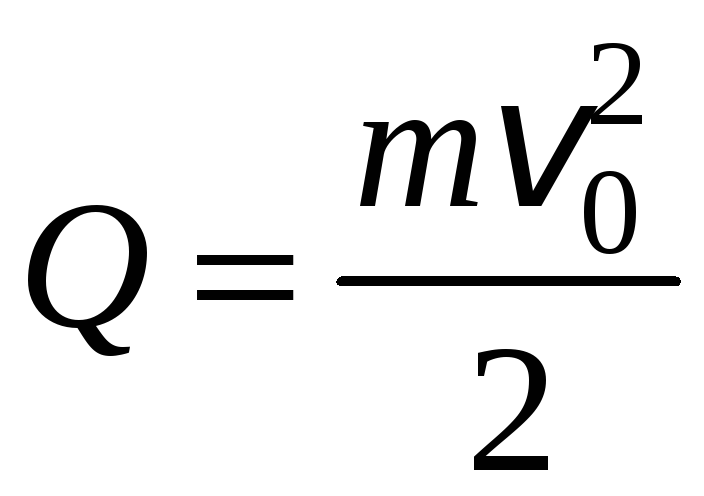 .
.
Ответ:
![]() ;
;
 .
.