30.11.06. Атом водорода. Модель Резерфорда-Бора.

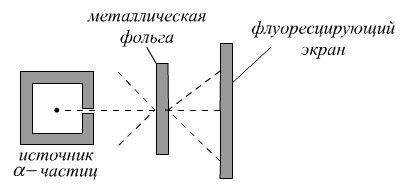
Опыты Резерфорда:

м. (радиус атома).

м. (радиус ядра).

Ядерная модель

Несостоятельность планетарной модели.

(излучение электромагнитной энергии диполем).

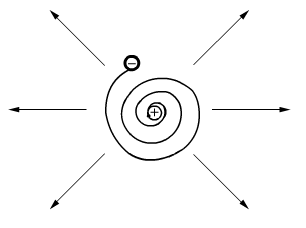
с.

Сплошной спектр.

Эксперимент.

Атом устойчив.

Спектр линейчатый.

Формула Бальмера:

, где - постоянная Ридберга,- целые числа.

- серия Лаймана.

- серия Бальмера.

- серия Пашена.

Модель Бора.

1). Существование стационарных орбит.

Квантование орбит.

(- момент импульса).

, - радиус орбиты.

, .

(- длина волны де Бройля).

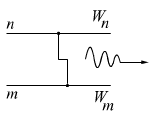
2). Квантование частот.

Переход электрона с одной орбиты до другой.

Размер атома водорода по Бору (расчет ).

,

(сокращая, получи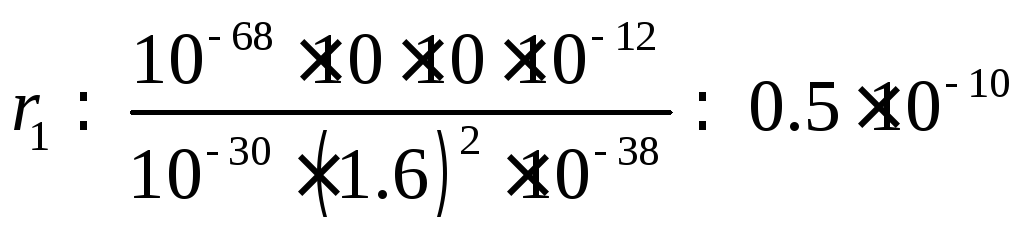м)

м.

,

, ,(- масса электрона).

- целые числа.

Квантовая теория атома водорода

(оператор Гамильтона).

Радиальная симметрия. Оператор Лапласа в сферических координатах.

, - константа нормировки,- неизвестная константа.

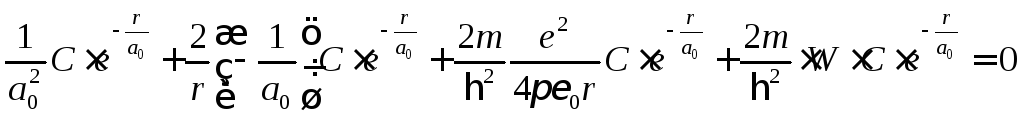
Выражение для не должно содержать.

(по Бору).

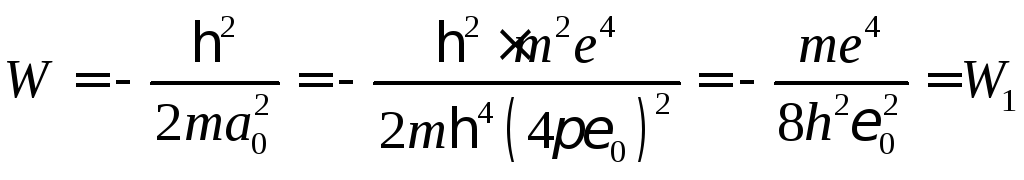(по Бору).

,

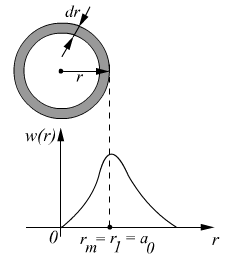
- вероятность того, что электрон окажется в шаровом слое радиуса и толщиной.

(плотность вероятности).

Берем производную от выражения без констант и приравниваем ее к нулю

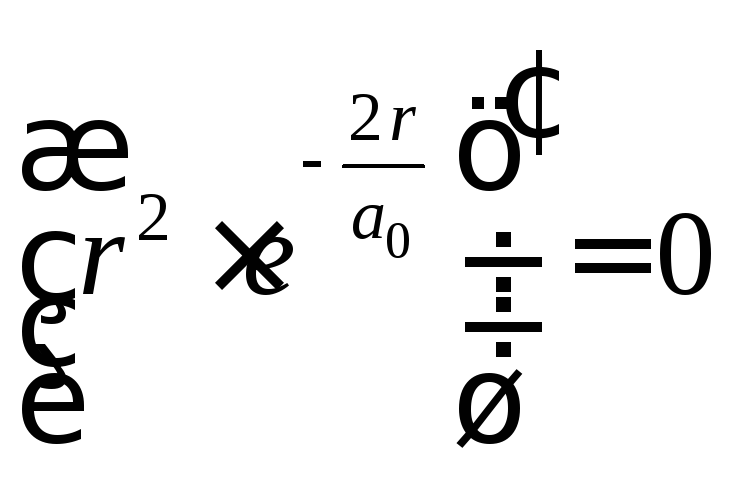
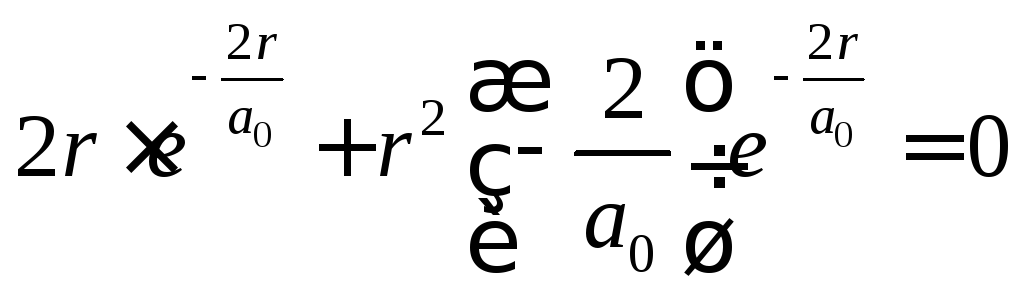
Сокращая, получаем:

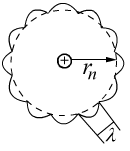
Расчеты показывают, что боровские стационарные орбиты с точки зрения кванто-механических представлений- это геометрическое место точек вокруг ядра, соответствующих максимальной вероятности нахождения электрона.

* Линейный осциллятор * (не будет в программе экзамена).

, ,- собственная частота.

, амплитуда.

,

.

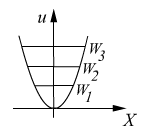
Следовательно, существует нулевая энергия осциллятора.

04.12.06. Линейный гармонический осциллятор.

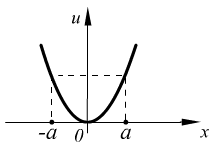
Классическое рассмотрение.

,

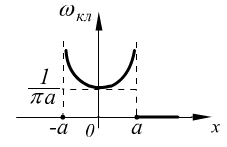
при

,

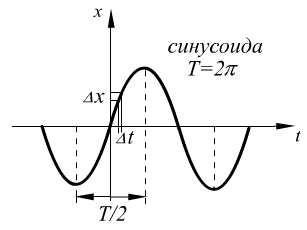
Квантовая теория.

,

Следовательно, ,(квантование энергии).

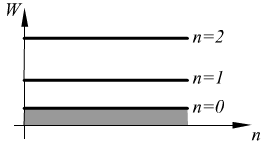
- нулевая энергия (её нельзя отнять осциллятором).

,

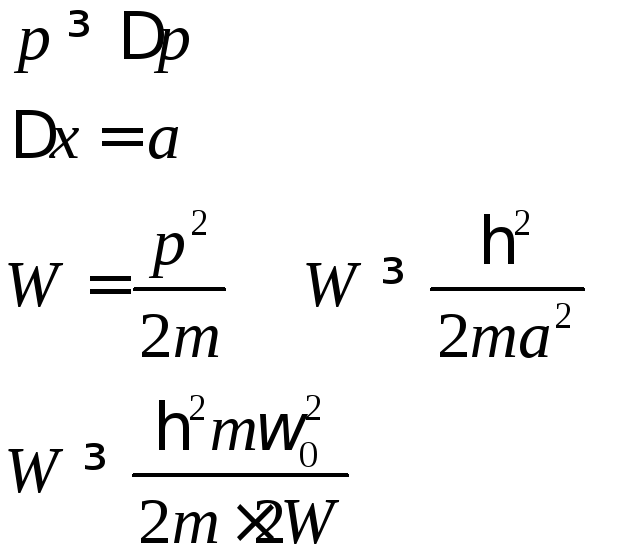
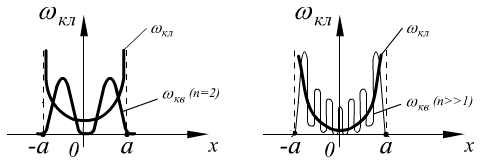
принцип соответствия

Состояние электронов в атомах.

- главное квантовое число.

- орбитальное квантовое число.

- магнитное квантовое число.

- спиновое квантовое число.

, .

- орбитальный момент импульса электрона.

- - состояние.

- - состояние.

- - состояние.

- - состояние.

- - состояние.

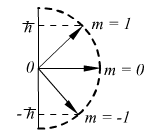
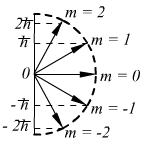
Магнитное квантовое число.

(пространственное квантование).

- орбитальное гиромагнитное отношение

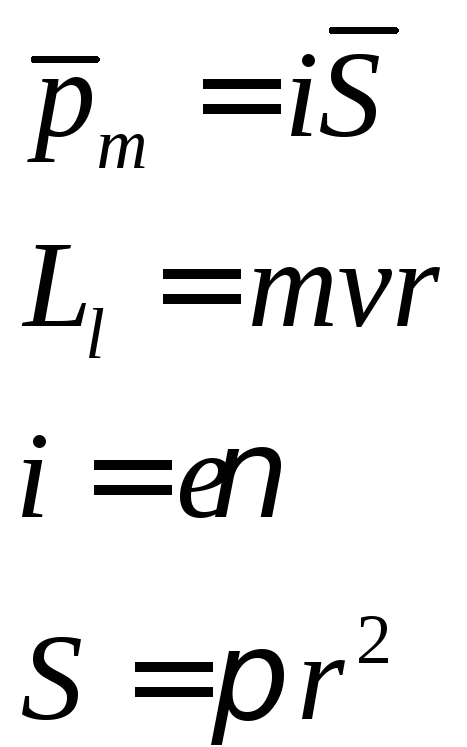
Внешнее магнитное поле вдоль .

, (пространственное квантование).

Опыты Штерна и Герлах. (1921г.).

(измерение магнитных моментов атомов).

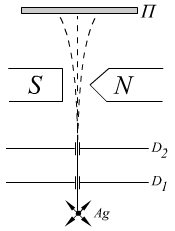
Нет поля

Поле есть

(классика) (размытая картина)

(воображение)

Поле есть

(квантовая теория)

Эксперимент

(квантовая теория)

Серебро: на внешней оболочке.

Следовательно, электрон обладает собственным моментом импульса и собственным магнитным моментом .

Спин электрона: ,,.

, ,

Принцип (запрет) Паули:

В атоме не может быть электронов с одинаковым набором четырех квантовых чисел.