3. Апланатические двухзеркальные системы

Апланатической двухзеркалъной системой рефлектора называется такая, в которой исправлена аберрация кома.

Впервые для частных случаев предфокальных укорачивающих систем эта задача была решена в 1905 г. К. Шварщпильдом. Решение для предфокальных удлиняющих систем дали Г. Ричи и Г. Кретьен. Си­стемы Ричи — Кретьена получают сейчас широкое распростране­ние. В 1923—1924 гг. Д. Д. Максутов выполнил общий анализ сферической аберрации и комы двухзеркальных систем, независимо от Шварцшильда, Ричи и Кретьена открыл апланати­ческие системы и рассмотрев разные типы их, указал на возмож­ность использования не только предфокальных, но и зафокальпых систем, что до него не было известно.

Все зафокальные аплапатические системы (β < 0, q < 0) назы­ваются системами Максутова, предфокальные удлиняющие (0< β < 1, q > 0)— системами Ричи— Кретьена, предфокальные укорачивающие (1< β, q > 0)— системами Шварцшильда (см. рис. 6).

Рис. 6. Оптическая схема апланатического рефлектора Д.Д. Максутова (а), его конструктивное исполнение (б) и схема рефлектора Шварцшильда (в).

Апланатические системы с исправленным астигматизмом получи­ли название систем Кудера.

ВЫВОД

В работе были рассмотрены основные типы зеркальных оптических телескопов, виды зеркальных асферических поверхностей, геометрические и оптические свойства поверхностей второго порядка. А также был составлен алгоритма расчета траектории произвольного луча, проходящего через действительный геометрический фокус выпуклого гиперболического зеркала.

Приложение а

Алгоритм расчета траектории произвольного луча, проходящего через действительный геометрический фокус выпуклого гиперболтческого зеркала.

Параметры гиперболического зеркала:

1. Световой диаметр D=1000 мм;

2. Радиус кривизны при вершине r₀=-1000 мм;

3. Эксцентриситет е=1,1

Запишем уравнение гиперболы:

Расстояние от т.О до фокусов гиперболы: и

Зададим уравнение прямой, проходящей через первый фокус гиперболы F₁ и произвольную точку М():

Составим уравнение нормали к гиперболе в точке М:

Тангенс угла α₁ наклона прямой f₁(z) к оси х равен коэффициенту k₁ в уравнении этой прямой:

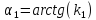
Тангенс угла α₂ наклона нормали n(z) к оси х равен коэффициенту k₂ в уравнении этой прямой:

Угол между прямой f₁(z) и нормалью n(z) равен:

Он должен быть равен углу α₃ между нормалью n(z)и прямой f₂(z), проходящей через точку М и второй фокус F₂. Следовательно, получим угол α₃ наклона прямой f₂(z) к оси х

Тогда коэффициент k₃ уравнения этой прямой будет равен тангенсу угла α₃:

Получим уравнение прямой f₂(z):

Прямая f₂(z) пересечет ось абсцисс в точке с координатой z=10000. Следовательно прямая f₂(z) пройдет через фокус F₂ гиперболы.

Список использованных источников информации

1. Пуряев Т.Д. Методы контроля оптических асферических поверхностей. М.: Машиностроение, 1976. 262с.

2. Михельсон Н.Н. Оптические телескопы. Теория и конструкция. М.: Наука, 1976. 512с.

3. Канатников А.Н., Крищенко А.П. Аналитическая геометрия. М.: Изд-во МГТУ им. Баумана, 2000. 388с.

4. Заказнов Н.П., Кирюшин С.И., Кузичев В.И. Теория оптических систем. М.:Машиностроение, 1992. 448 с.