
5.5 Рациональные сечения
Для повышения жесткости без увеличения массы деталей необходимо усиливать участки сечений, подвергающиеся при данном виде нагружения наиболее высоким напряжениям, и удалять ненагруженные и малонагруженные участки. При изгибе напряжены сечения, наиболее удаленные от нейтральной оси. При кручении напряжены внешние волокна; по направлению к центру напряжения уменьшаются и в центре они равны нулю. Следовательно, целесообразно всемерно развивать наружные размеры, сосредоточивая материал на периферии и удаляя его из центра. Наибольшей жесткостью и прочностью при наименьшей массе обладают развитые по периферии полые тонкостенные детали типа коробок, труб и оболочек.
Таблица 5.5 Прочность, жёсткость и масса профилей
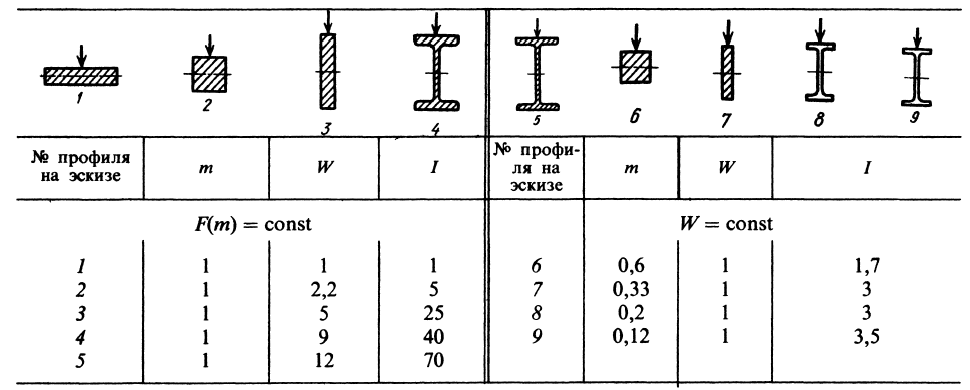
В табл. 5.5 приведено сравнение показателей различных профилей при изгибе. В основу сравнения положены условия равенства масс (сечений F) и прочности (моментов сопротивления W). Увеличение прочности и жесткости достигается последовательным применением принципа разноса материала в область действия наибольших напряжений. За единицу приняты масса, моменты сопротивления и инерции исходного профиля 1, у которого материал сосредоточен вблизи нейтральной оси. Придание наиболее целесообразной двутавровой формы профилям одинаковой массы (эскизы 1—5) увеличивает их прочность в 9 — 12 раз, а жесткость в 40—70 раз по сравнению с исходным профилем. Для профилей, одинаковой с исходным профилем прочности (эскизы 6—9), придание двутавровой формы снижает массу до 0,2—0,12 и повышает жесткость в 3—3,5 раза по сравнению с исходным профилем. Зависимость между массой, прочностью и жесткостью цилиндрических валов с разным отношением d/D приведена на рис. 4.3.2.
Таблица 5.5.1 Влияние диаметра вала на параметры конструкции

В качестве конструктивного примера в табл. 5.5.1 представлен вал зубчатого колеса, установленный на подшипниках качения, и приведены сравнительные показатели жесткости (I), прочности (W), массы (G), удельной прочности (W/G) и долговечности (h) подшипников при последовательном увеличении диаметра вала (и размера подшипников). За единицу приняты показатели массивного вала.
П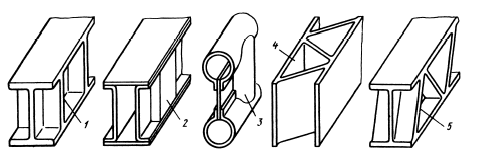 овышение
поперечной жёсткости.
С увеличением наружных размеров деталей
и уменьшением толщины их стенок
необходимо во избежание местных
деформаций повышение жёсткости в
направлении, поперечном действию
изгибающих моментов.
овышение
поперечной жёсткости.
С увеличением наружных размеров деталей
и уменьшением толщины их стенок
необходимо во избежание местных
деформаций повышение жёсткости в
направлении, поперечном действию
изгибающих моментов.
Рис. 5.5
На рис. 5.5 показано усиление балок поперечными рёбрами 1, коробками 2, полукруглыми накладками 3, косыми связями 4,5.
Оребрение. Для увеличения жёсткости, особенно литых и сварных корпусных деталей, широко применяют оребрение. При этом следует правильно выбирать соотношение сечений рёбер и оребряемой детали, иначе вместо упрочнения можно получить обратный эффект.
У деталей, подвергающихся изгибу в плоскости расположения наружных рёбер (рис. 5.5.1), на вершине ребра возникают напряжения растяжения, достигающие большой величины вследствие малой ширины и малого сечения ребра. Особенно опасны тонкие рёбра, суживающиеся к вершине (рис. 5.5.1, б, в). Разрушение начинается с разрыва вершины ребра. Прочность значительно возрастает при утолщении рёбер, особенно на опасном участке, т. е. у вершины ребра (рис. 5.5.1, г, д). Ослабление детали рёбрами формально выражается в уменьшении момента сопротивления сечения детали.
На рис. 5.5.2 показаны: исходная высота детали – b0 , исходная толщина стенки детали - h0, высота ребра – h, толщина ребра – b, шаг рёбер – t.

Рис. 5.5.1 Формы рёбер Рис. 5.5.2 К определению формы рёбер
Введение рёбер во всех случаях увеличивает момент инерции сечения и, следовательно, жёсткость детали на изгиб. Этот эффект тем больше, чем больше высота и толщина рёбер. Иная картина получается для моментов сопротивления, если сечение рёбер мало в сравнении с сечением детали.
Если обозначить
![]() =
h/h0
и t0
= b0/b,
то момент сопротивления сечения в
неблагоприятном случае (
=
h/h0
и t0
= b0/b,
то момент сопротивления сечения в
неблагоприятном случае (![]() =2;
t0
=100) уменьшается
по сравнению с исходным профилем в 3
раза.
=2;
t0
=100) уменьшается
по сравнению с исходным профилем в 3
раза.
Как это ни кажется
парадоксальным, удаление таких рёбер
упрочняет деталь. Для практического
определения максимально допустимого
шага рекомендуется исходить из
соотношения
![]() .
(5.5.1)
.
(5.5.1)
 Рёбра
с относительной величиной
Рёбра
с относительной величиной
![]() не уменьшают прочность детали.
не уменьшают прочность детали.
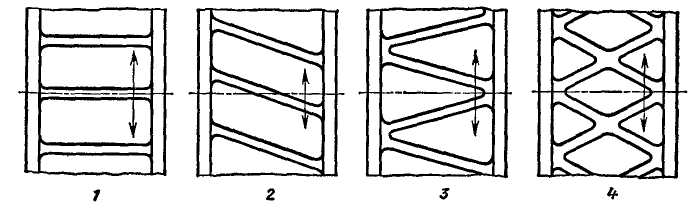
Рис. 5.5.3 Оребрение илиндрических деталей, работающих на кручение.
При нагружении цилиндрических и близких к ним по форме деталей крутящим моментом продольные прямые ребра (1) крайне незначительно увеличивают жесткость детали (рис. 5.5.3). Скорее такие ребра вредны, так как они подвергаются изгибу (в плоскости, перпендикулярной грани ребер), вызывающему в них повышенные напряжения. При одностороннем кручении выгодно применять косые ребра 2, которые под действием крутящего момента работают на сжатие, сильно увеличивая жесткость детали (частный случай применения принципа раскосных связей).
При крутящем моменте переменного направления целесообразно располагать ребра змейкой (3) или крестообразно (4). Косые и спиральные ребра менее подвержены внутренним напряжениям, возникающим при усадке в результате неравномерного охлаждения отливки. Однако формовка косых ребер на наружных цилиндрических, конических и тому подобных поверхностях затруднительна.
Жёсткость машиностроительных конструкций
Главными средствами повышения жёсткости деталей и конструкций без увеличения массы изделия или даже со снижением её являются:
придание стенкам конструкции сводчатых форм, рациональное оребрение, введение между стенками связей (предпочтительно диагональных), скругление переходов, уход (по возможности) от консольных нагрузок, разработка моноблочных конструкций корпусов и рам, ….
В таблице 5.6 приведены примеры повышения жёсткости некоторых простых конструкций [36].
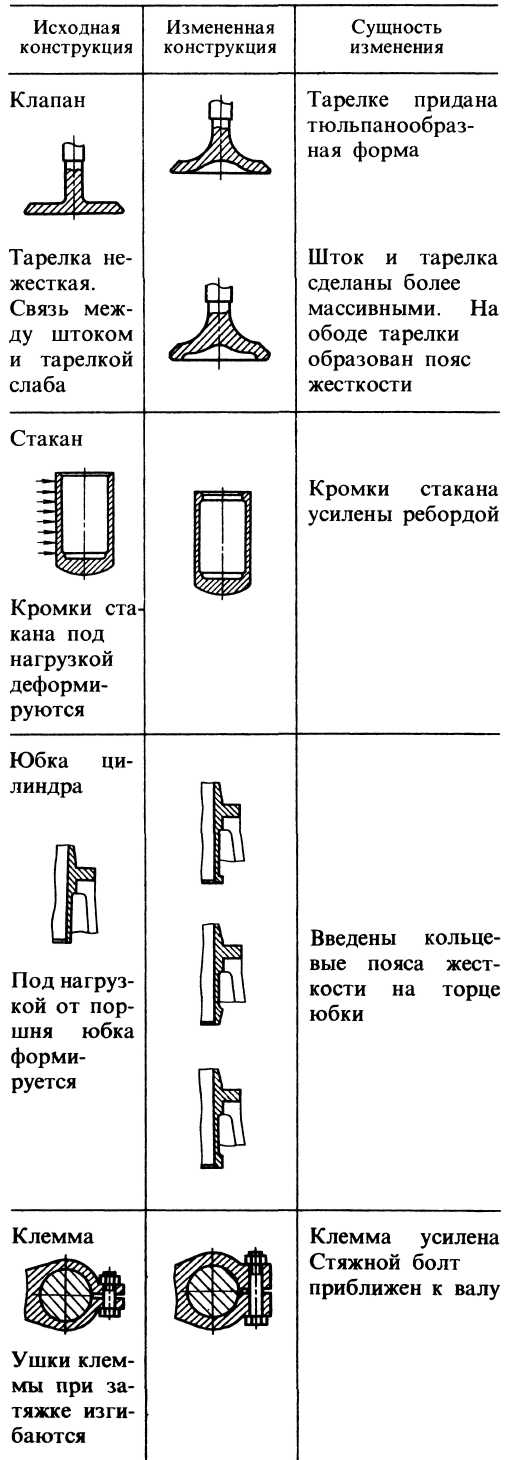 Таблица 5.6
Продолжение табл. 5.6
Таблица 5.6
Продолжение табл. 5.6
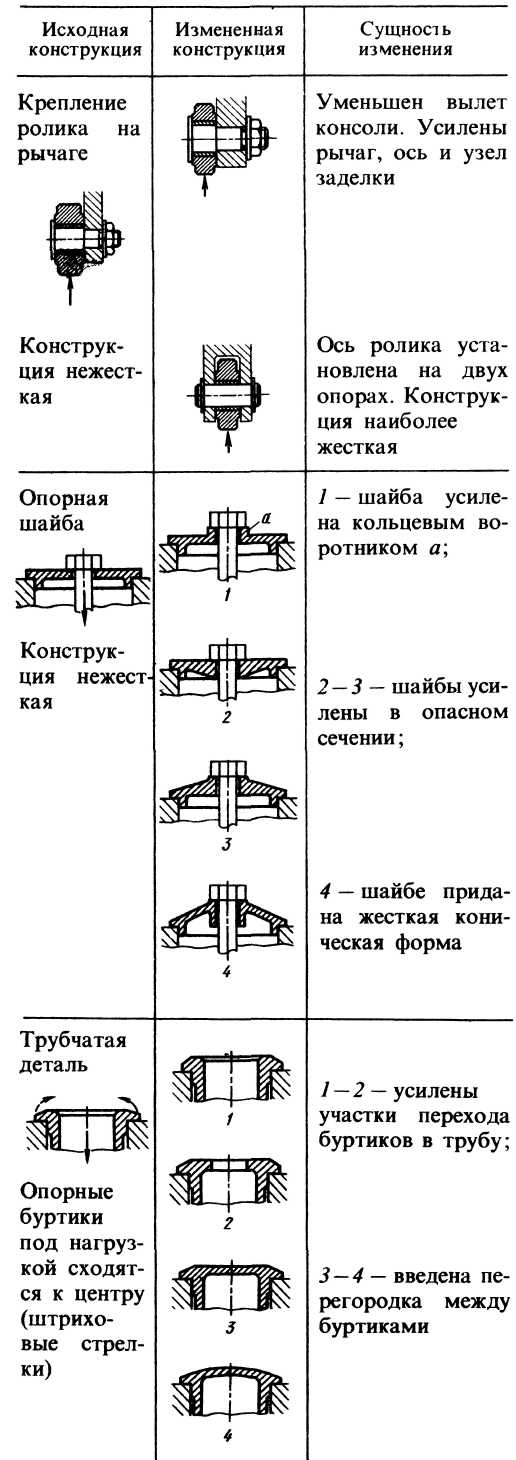
Таблица 5.6 Увеличение жёсткости конструкций
Продолжение табл. 5.6
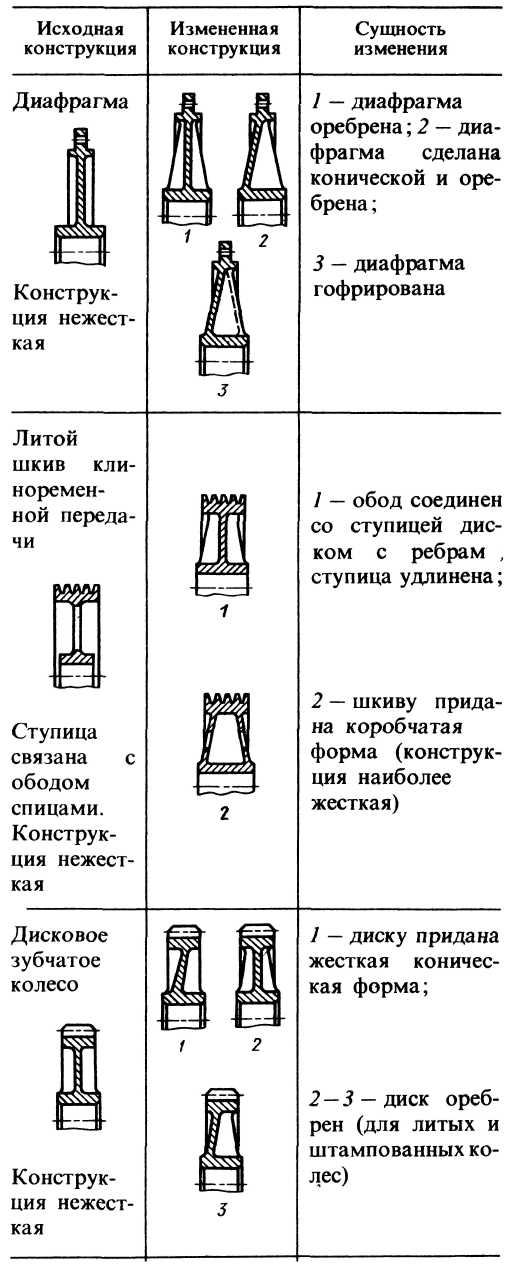
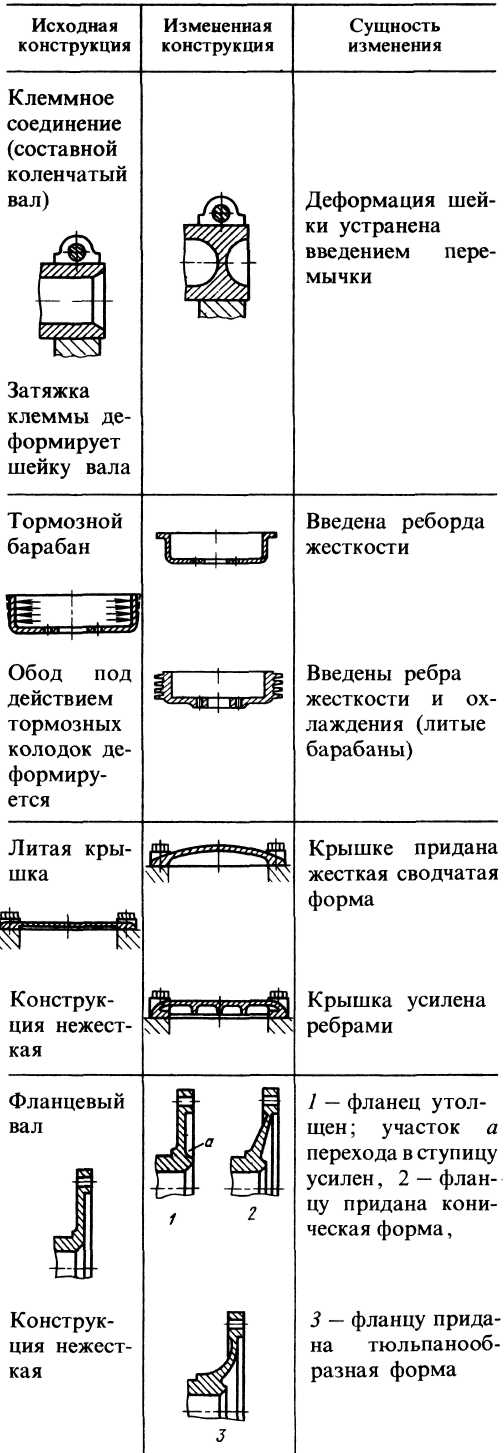

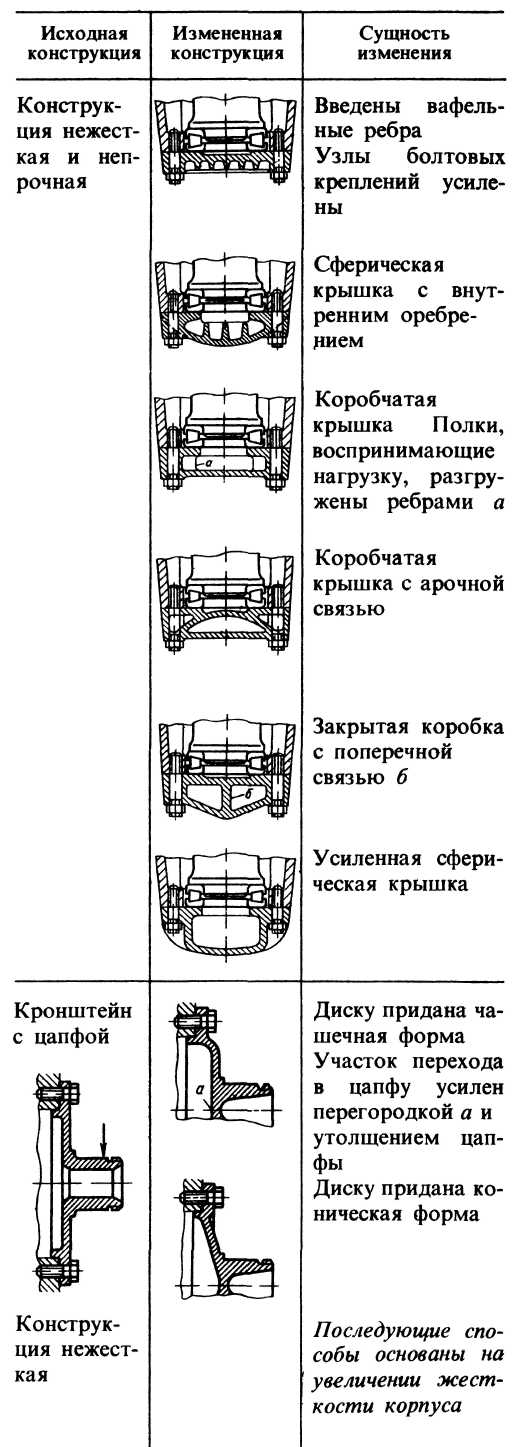 Продолжение
табл. 5.6
Продолжение
табл. 5.6
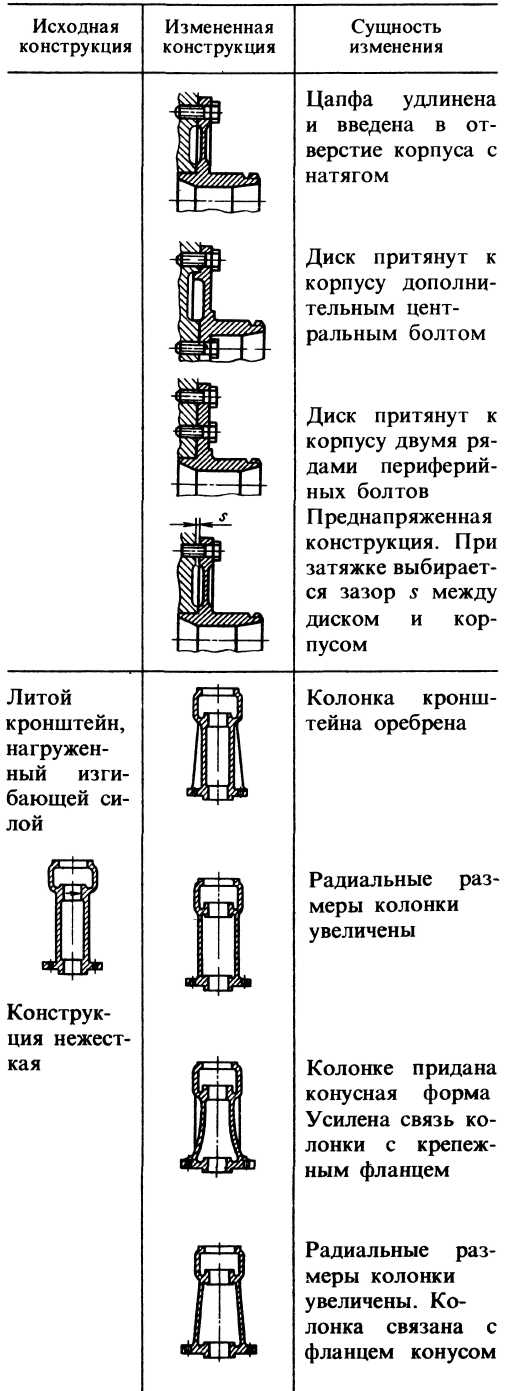
 Продолжение
табл. 5.6
Продолжение
табл. 5.6
Продолжение таблицы 5.6

Продолжение таблицы 5.6
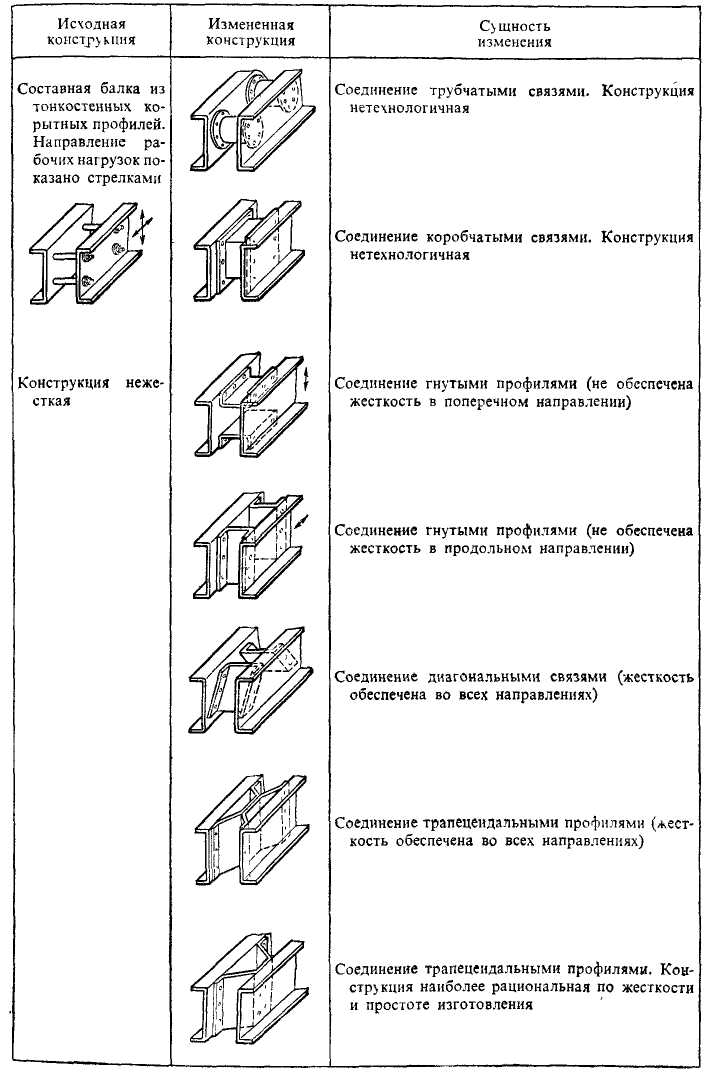
Продолжение таблицы 5.6
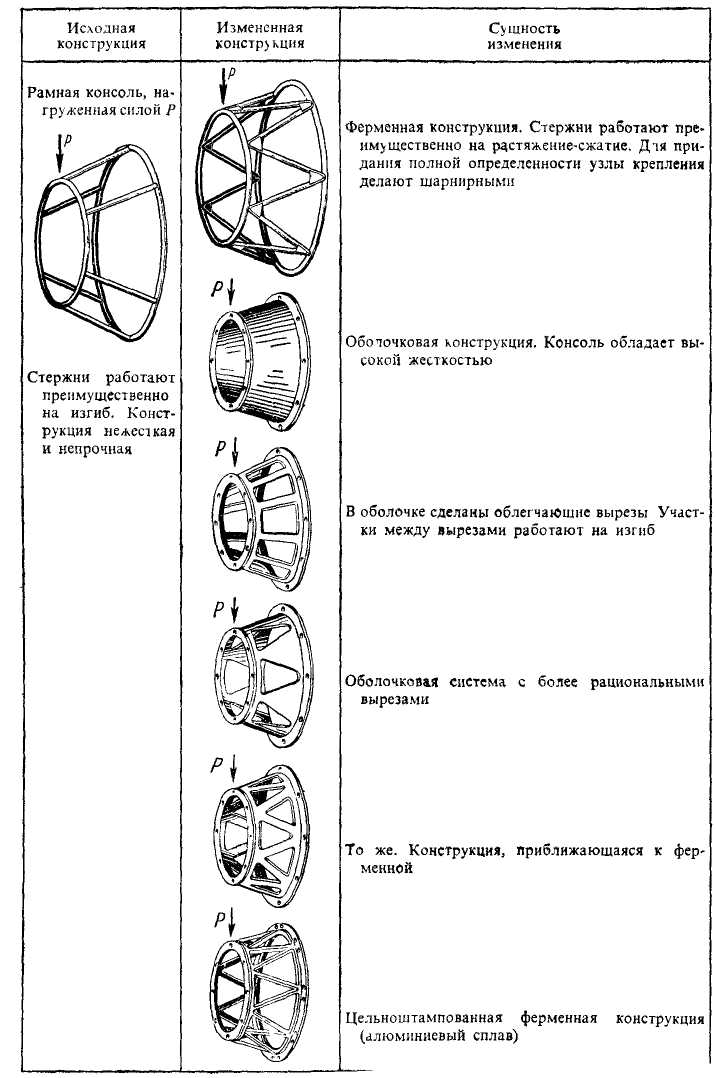
Р —
сосредоточенная
сила или полная нагрузка ;
р — интенсивность
сплошной нагрузки;
L
— внешний изгибающий
момент , Q
— поперечная
сила ; М —
изгибающий момент;
v
— прогиб в сечении
с координатой х
;
![]() — угол поворота на конце балки в радианах;
— угол поворота на конце балки в радианах;
f = vmax—стрела прогиба, Е—модуль продольной упругости материала балки. Предполагается, что горизонтальная ось, проведенная в поперечном сечении через его центр тяжести, совпадает с главной осью сечения; по отношению к ней момент инерции обозначен I, max (-М) обозначен отрицательный момент с наибольшим абсолютным значением.
Правило знаков. Реакции, направленные вверх, поперечная сила Q и изгибающий момент М, действующие на левую часть балки соответственно вверх и по часовой стрелке, считаются положительными; прогиб вниз и угол поворота по часовой стрелке считаются положительными
Схема балки и нагрузки |
||||
1. Статически определимые балки |
||||
1.Консоль. Сила на конце
|
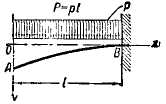
2. Консоль. Сплошная равномерная нагрузка
|
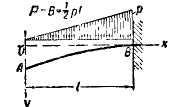
3. Консоль. Сплошная нагрузка по треугольнику
|
||
Опорные реакции и поперечные силы |
||||
В = P; Q = -P; |
B = P = pl; Q = - Px / l; |
B = P = Pl / 2; Q = -Pl / x; |
||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
||||
M = -Px; max M = 0; max(- M) = -Pl; (в В) |
|
|
||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
||||
|
|
(в А). |
||
Продолжение табл. 5.7
Схема балки и нагрузки |
||||
|
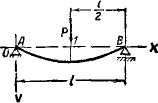
5. Балка, свободно опертая по концам. Сила в середине пролета
|
6. Балка, свободно
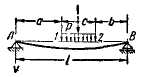
опёртая по концам. Сила в пролёте
|
||
Опорные реакции и поперечные силы |
||||
B = 0;
Q = 0; |
|
A
=
|
||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
||||
M = -L;
max (-M) = -L; (от А до В) |
|
; (в В); (в А);
|
||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
||||
θ
= |
(от А до 1);
f
=
|
прогиб при
|
||
Продолжение табл. 5.7
Схема балки и нагрузки |
|||||
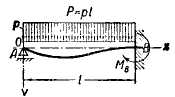
7. Балка, свободно опертая по концам. Сплошная равномерная нагрузка
|
8. Балка, свободно опертая по концам. Сплошная равномерная нагрузка р части пролёта d =b + c/2
|
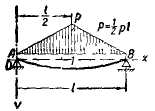
9. Балка, свободно опертая по концам. Нагрузка по треугольнику
|
|||
Опорные реакции и поперечные силы |
|||||
|
|
A
=
|
|||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|||||
M
=
max
(M)
=
(при x = l/2); |
(от1 до 2)
(от 2 до В);
|
(при x = 0.577l);
|
|||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|||||
|
Формулы для определения v и θ см. стр. 132
|
|
|||
Схема балки и нагрузки |
|||||
10. Балка, свободно опёртая по концам. Нагрузка по треугольнику
|
11. Балка, свободно опёртая по концам. Момент над опорой
|
12. Балка, свободно опёртая по концам. Момент в пролёте
|
|||
Опорные реакции и поперечные силы |
|||||
(от 1 до В); |
|
;
|
|||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|||||
(от А до1);
(от 1 до В); max (M) = Pl / 6 (в 1); |
|
; (от А до 1) ; (от 1 до В);
|
|||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|||||
θ
= |
(при x=0.422l);
|
(от А до 1);
|
|||
Продолжение табл. 5.7
Схема балки и нагрузки |
|||||
13. Свободно опёртая балка с одной консолью, нагруженной на конце
|
14. Свободно опёртая балка с двумя равными консолями. Нагрузка сплошная равномерная. Расстояние x принято от точки О
|
15. Один конец свободно опёрт, другой защемлён. Сила в середине ( Далее в схемах нагрузки балки постоянного сечения с жёсткой заделкой)
|
|||
Опорные реакции и поперечные силы |
|||||
(при 0 < x1 < c ); |
при (l+c) > x >c);
|
|
|||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|||||
max (M) = 0;
|
при (l+c)>x>c;
|
(от 1 до В);
|
|||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|||||
(от А до В);
(при 0 < x1 < c);
(при x=0.578l 1);
|
Уравнение упругой линии может быть составлено на основании принципа наложения из выше указанных схем нагрузок. Точка перегиба упругой линии при
|
(от А до 1);
|
|||
Продолжение табл. 5.7
Схема балки и нагрузки |
|||||
|
17. Один конец свободно опёрт, другой жёстко защемлён. Сплошная равномерная нагрузка
|
18. Один конец свободно оперт, другой жёстко защемлён. Момент над свободной опорой
|
|||
Опорные реакции и поперечные силы |
|||||
(от А до
1);
|
|
|
|||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|||||
(от А до1);
( от1 до В );
max (M) = Ab ( в 1); |
|
|
|||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|||||
(при x=0.586 1);
|
|
(от А до 1);
|
|||
Продолжение табл. 5.7
Продолжение табл. 5.7
Схема балки и нагрузки |
|||||
18. Один конец свободно оперт, другой жёстко защемлён. Момент над свободной опорой
|
19. Один конец свободно опёрт, другой жестко защемлён. Момент в пролёте. Расстояние точки 1 приложения момента L от левой опоры обозначено а
|
20. Оба конца жестко защемлены. Сила в середине
|
|||
Опорные реакции и поперечные силы |
|||||
|
(от А до В);;
|
|
|||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|||||
( от1 до В ); max (M) = Ab ( в 1); |
;
; (в В );
|
(от А до 1);
(в 1 справа);
|
|||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|||||
при x = l /3;
|
(от А до 1);
(от 1 до В);
|
|
|||
Схема балки и нагрузки |
|||||
21. Оба конца жестко защемлены. Сила в пролете
|
22. Оба конца жёстко защемлены. Сплошная равномерная нагрузка
|
23. Оба конца жёстко защемлены. Момент в пролёте на расстоянии а от левой опоры
|
|||
Опорные реакции и поперечные силы |
|||||
; ( от 1 до В);
|
|
; |
|||
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|||||
(от А до1);
|
|
(от А до 1); ; (от 1 до В);
(в 1 справа); (в В);
|
|||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|||||
(от А до 1) ;
при
x
=
при
x
=
|
|
(от А до 1); наибольший по величине прогиб вверх; (вниз)
при
(при
(в 1); |
|||
Продолжение табл. 5.7
Схема балки и нагрузки |
|
Влияние смещения опор и изменения температуры |
|
24. Один конец свободно опёрт, другой жестко защемлен. Осадка свободной опоры 1 см
|
25. Один конец свободно опёрт, другой защемлён. Поворот защемленного конца А на угол 1 радиан
|
Опорные реакции и поперечные силы |
|
|
; ;
|
Уравнение изгибающего момента; величина и место наибольшего изгибающего момента |
|
|
|
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
|
|
(
в
А ) ;
|
Продолжение табл. 5.7
Формулы к схеме нагрузки 8
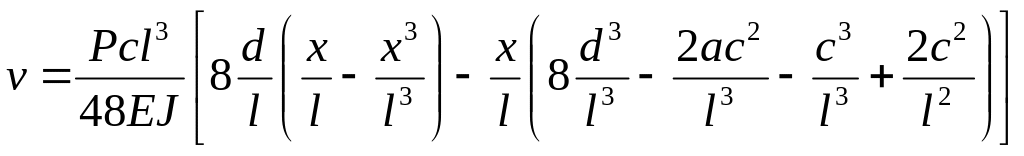 (от
А до 1);
(от
А до 1);
 (от
1 до 2);
(от
1 до 2);
![]() (в А );
(в А );
Схема балки и нагрузки |
||||
26. Оба конца
жёстко защемлены. Поворот защемлённого
конца А на угол 1радиан
|
27. Оба конца не поворачиваются. Осадка левой опоры на 1 см
|
28. Один конец закреплен на подвижной шарнирной опоре, в другой жестко защемлён
|
||
Опорные реакции и поперечные силы |
||||
Q
=
|
|
A=-B
=
|
||
Уравнение изгибающего момента; величина к место наибольшего изгибающего момента |
||||
M= (2EJ/l)(2-3x/l);
max M = 4EJ/l (в А);
max (-M) = -2EJ/l (в В) |
|
; (в В); (в А);
|
||
Уравнение упругой линии, стрела прогиба, углы поворота концов балки |
||||
θ =1 (в А); θ =0 (в В) |
f=1 (в А);
|
прогиб при
|
||
Продолжение табл. 5.7






 .
.





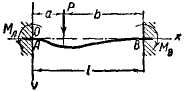
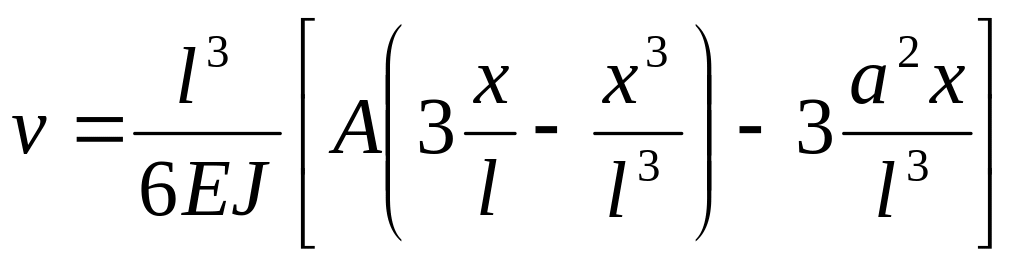 (от
А до 1);
(от
А до 1);



 ;
;

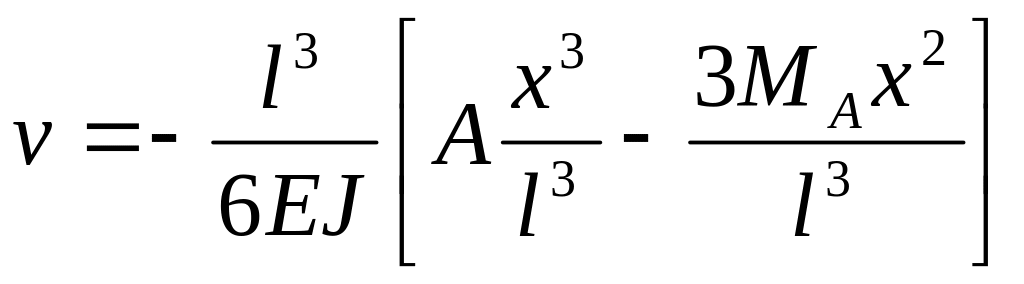 ;
;


