Задача 5

Установить изме­нение условий статической устойчивости по напряжению узла на­грузки с девятью асинхронными двигателями (рис 9.27, а) при включении конденсаторной батареи, которая имеет в исходном режиме мощность, равную компенсирующей способности синхронных двигателей из предыдущего примера. Исходные данные для расчета указаны на рисунке; активная мощность, потребляемая узлом на­грузки, и параметры внешней сети в именованных единицах соответствуют данным, приведенным в предыдущем примере.

Решение. За базисные принимаем условия для шин узла нагрузки:

U_*б = U /U_б = 6 / 6 = 1; S_б = P_{а.дв.ном} / (η cos φ_ном) =

= 9 ∙ 0,63 / (0,935 ∙ 0,89) = 6,8 МВА.

Так как численные значения базисных величин совпадают с принятыми в задаче 4, то

Z_*вн = 0,1983 + j0,1919.

Рис. 9.27. К задаче 5

Параметры эквивалентного асинхронного двигателя:

для номинального режима

P_{*а.дв.ном} = Р_{а.дв.ном} / (η S_б) = 9∙ 0,63 / (0,935 ∙ 6,8) = 0,892;

Q_{*а.дв.ном} = Р_{*а.дв.ном} tg φ_ном = 0.892 tg (arcos 0,89) = 0,457;

для исходного режима

Р_*а.дв = m P_{*a.дв1.ном} =0,87∙0,892 = 0,777;

Q_*а.дв = Q_{*а.дв.1 ном} [c + m /((m_max /m + tg φ_ном)],

где

Активная мощность, которая поступает в узел нагрузки от ГПП,

Р_*с = Р_*а.дв = 0,777,

а реактивная мощность (при отсутствии компенсации ее в узле нагрузки)

Q_c1 = Q_*а.дв = 0,399.

Реактивная мощность при подключении конденсаторной батареи к узлу на­грузки

Q_*c2 =Q_*а.дв – Q_*к.б = 0,399 – 0,263 = 0,136.

Напряжение на шинах ГПП в исходном режиме:

при отсутствии компенсации реактивной мощности

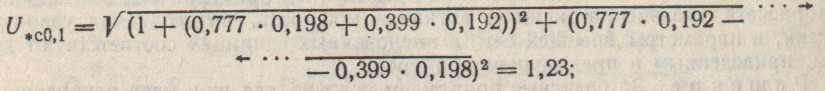
при подключении конденсаторной батареи

Реактивная мощность, поступающая от ГПП,

Реактивная мощность эквивалентного асинхронного двигателя

Реактивная мощность, вырабатываемая конденсаторной батареей,

Q_*к.б ( U_* ) = Q_{*к,б.ном} U²_* = 0,263 U²_* .

Результаты расчета составляющих баланса реактивной мощности при раз­личных напряжениях в узле нагрузки сведены в табл.9.6 и отражены на рис. 9.27.

Из уравнений Δ Q_*c1 = Q_*c1 – Q_{* а.дв}; ΔQ_*c2 = Q_*c2 + Q_*к.б – Q_*а.дв

находим значения критического напряжения: при отсутствии компенсации U_*кр1 = 0,745; при включении конденсаторной батареи U_*кр2 = 0,76.

Таким образом, включение конденсаторной батареи снижает требования к уровню напряжения на шинах ГПП, но ухудшает условия статической устойчи­вости узла нагрузки: запас устойчивости снижается с К_3U1 = 100 (1 — 0,745) = 25,5 % до К_3U2 = 100 (1 — 0,76) = 24 %.

Сравнение этих результатов с результатами, полученными в предыдущем примере, показывает, что замена части асинхронных двигателей синхронными более предпочтительна для снижения требований к уровню напряжения на ши­нах ГПП и обеспечения достаточного запаса статической устойчивости узла на­грузки.

Таблица 9.6.Результаты расчета составляющих баланса реактивной мощности при различных значениях напряжения в узле нагрузки

9.4. Устойчивость узлов нагрузки при сильных возмущениях. Задача 1

Определить предельный угол снятия наброса нагрузки на синхронный электродвигатель при периодически меняющейся нагрузке от холостого хода до максимальной, график которой изображен на рис.9.28.а. При момент , .

Решение: Предельный угол снятия наброса нагрузки при согласно формуле

;

.

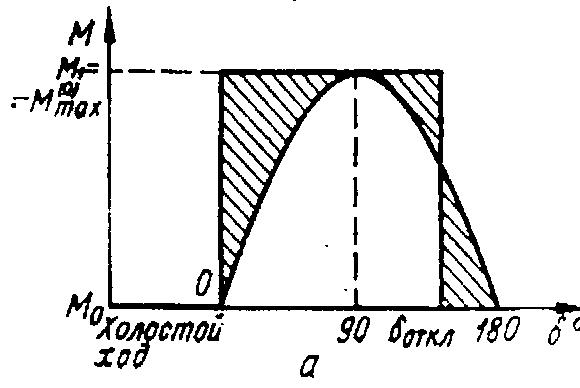
Рис.9.28.Угловые характеристики мощности

синхронного при увеличении момента сопртивления

Следовательно, при предельный угол рад, или

Если , то угол рад, или

(рис. 9.28,б).