Т. К. , то уравнение динамики можно записать в виде:

.

Или

.

Принимая

,

получим

.

Это уравнение идентично уравнению (2), решение которого известно. В переменных  оно будет иметь вид:

.

Из этого уравнения следует, что при малых колебаниях физический маятник совершает гармонические колебания с периодом:

,

где – приведенная длина физического маятника.

Точка О΄ на продолжении оси ОС, отстоящая от точки О на расстоянии L, называется центром качания физического маятника.

Применив теорему Штейнера, можно показать, что ОО΄ всегда больше . Точка подвеса О и центр качания О΄ взаимозаменяемы: если ось подвеса сделать проходящей через центр качаний, то точка О прежней оси подвеса станет новым центром качаний, и период колебаний физического маятника не изменится. Такой маятник называется оборотным.

Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Лабораторная работа 4.1 определение положения центра тяжести физического маятника

Цель работы: исследуя колебания физического маятника, рассчитать положение его центра тяжести.

Приборы и принадлежности: физический маятник, секундомер, линейка, призма, электромагнит, источник постоянного тока.

Вывод рабочих формул и описание установки

Ф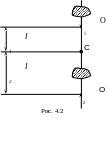 изический маятник, используемый в данной работе, представляет собой цилиндрический стержень, на котором закреплены две треугольные ножевые опоры и два дугообразных груза (чечевицы) (рис. 4.2).

Маятник устанавливается ножевой опорой на “подушки”, смонтированные на горизонтальной закрепленной планке.

Из теории следует, что

, , (1)

откуда

(2)

где

Решив уравнения (1) и (2), получим:

. (3)

Согласно теореме Гюйгенса-Штейнера,

,

где I₀ – момент инерции маятника относительно оси вращения, проходящий через его центр тяжести С.

Следовательно,

, (4)

где l – расстояние между первой и второй точками подвеса:

.

Приравнивая правые части полученных равенств (3) и (4) и учитывая, что , получим:

. (5)

Порядок выполнения работы

1. Установить маятник ножевой опорой на “подушки”.

2. Включить источник постоянного тока. Установить напряжение 12 В.

3. Отклонить маятник в сторону магнита до фиксации его положения.

4. Включить секундомер (при этом электромагнит отключается) и определить время 10 полных колебаний t₁.

5. Аналогичные измерения проделать 5 раз.

6. Выключить источник постоянного тока. Снять маятник, перевернуть его и установить на “подушки” второй ножевой опорой.

7. Проделать аналогичные измерения, определив время 10 полных колебаний t₂.

8. Вычислить периоды колебаний Т₁ и Т₂ по формуле 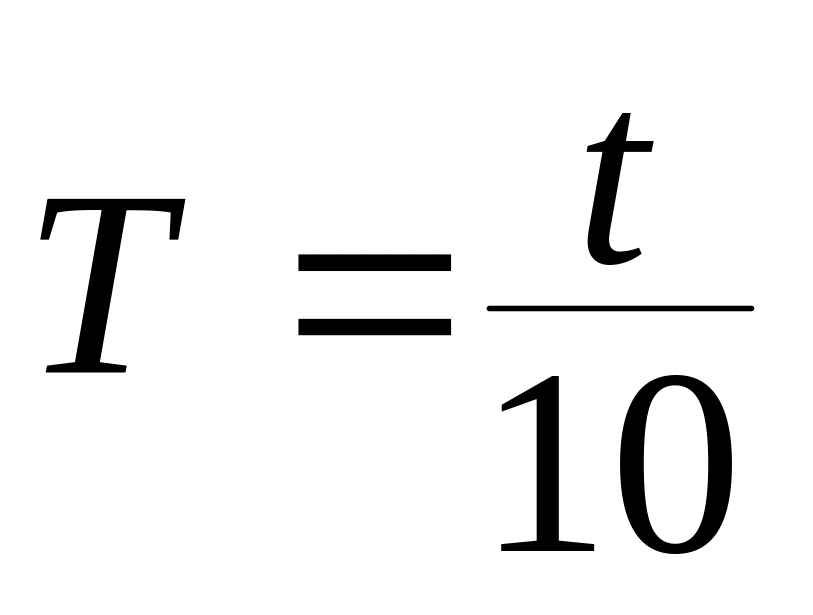и определить погрешности измерений.

9. Результаты измерений занести в таблицу:

№ п/п	t1, с	Δ t1, с	t2, с	Δ t2, с	Т1, с	Δ Т1, с	Т2, с	Δ Т2, с
1
2
3
4
5
Ср. знач.

10. Снять маятник, положить его на треугольную призму и, добившись равновесия, измерить линейкой расстояния от центра тяжести до ножевых опор l^'₁ и l^'₂, а также расстояние между точками подвеса (ножевыми опорами) l.

11. Вычислить приведенные длины физического маятника:

.

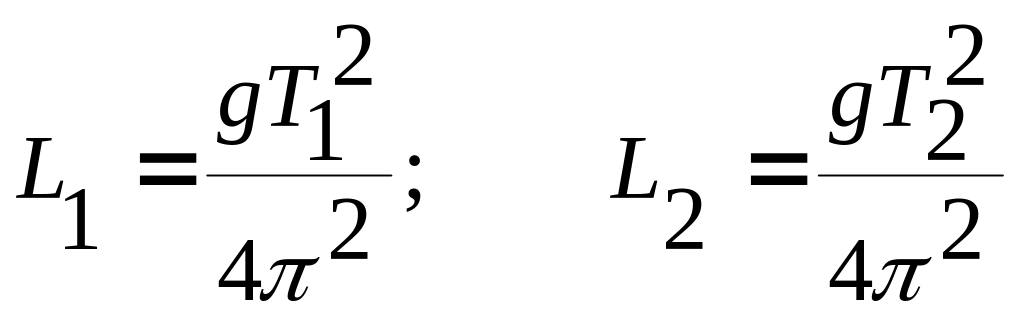12. Вычислить положение центра тяжести по формулам:

,

и сравнить их с l^'₁ и l^'₂, т. е. найти погрешности определения l₁ и l₂ относительно “истинных” значений l^'₁ и l^'₂:

.

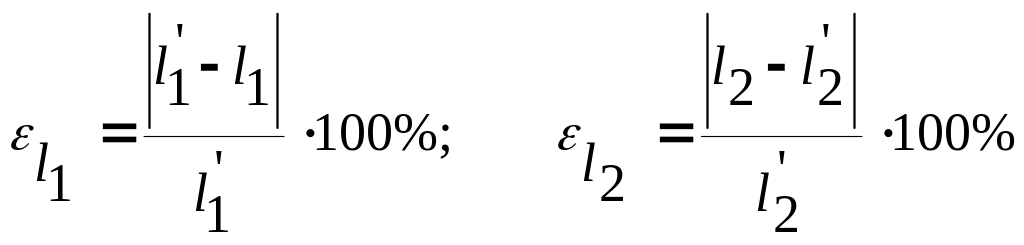13. Вычислить моменты инерции маятника (масса маятника указана на чечевице):

.

14. Результаты вычислений занести в таблицу, оценив погрешности косвенных измерений для l₁, l₂, I₁, I₂.

№ п/п

I1, кг∙м2

ε1,%

ΔI1, кг∙м2

I2, кг∙м2

ε2 %

ΔI2, кг∙м2

l1, м

εl1%

Δl1 м

l2,м

εl2%

Δl2 м

15. Сделать выводы.