Вопрос 24. Работа по перемещению проводника с током в магнитном поле. Понятие магнитного потока. Потокосцепление.

Поток вектора магнитной индукции.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная dΦB = BdS = BndS, где Bn = cos Bα — проекция вектора B на направление нормали n к площадке dS , α — угол между векторами n и B, dS — вектор, модуль которого равен dS , а направление совпадает с направлением нормали n к площадке.

Поток вектора B может быть как положительным, так и отрицательным в зависимости от знака cosα.

Поток вектора B связывают с контуром, по которому течет ток. Положительное направление нормали к контуру связано с направлением тока по правилу правого винта. Поэтому магнитный поток, создаваемый контуром

с током через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции через произвольную поверхность S: ΦB =∫B dS =∫ B n dS.

Если поле однородно и перпендикулярно ему расположена плоская поверхность с площадью S , то ΦB = BS.

Единица магнитного потока — вебер (Вб): 1Вб — магнитный поток, проходящий сквозь плоскую поверхность площадью 1м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1Тл (1 Вб=1 Тл·м2).

Потокосцепление.

Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потокосцеплением Ψ этого контура. Потокосцепление контура, обусловленное магнитным полем тока в самом этом контуре, называется потокосцеплением самоиндукции. Например, найдем потокосцепление самоиндукции соленоида с

сердечником с магнитной проницаемостью μ. Магнитный поток сквозь один виток соленоида площадью S равен Φ1 = BS . Полный магнитный поток, сцепленный со всеми витками соленоида равен:

Ψ = Φ1N = BSN = μoNI/ l * SN = μoμN^2I/l * S

Потокосцепление контура, обусловленное магнитным полем тока, идущего в другом контуре, называется потокосцеплением взаимной индукции этих двух контуров.

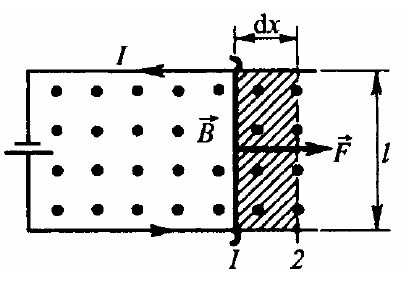
Работа по перемещению проводника с током в магнитном поле.

Проводник длиной l (он может свободно перемещаться) с током I находится в однородном магнитном поле (см. рисунок). Поле направлено перпендикулярно плоскости рисунка — из-за чертежа. Сила Ампера F = IBl. Под ее действием проводник переместился из положения 1 в положение 2. Работа, совершаемая магнитным полем:

dA = Fdx = I dx[l ,B] = IBldx = IBdS = IdΦ.

Использованы соотношения:

dS = ldx — площадь, пересекаемая проводником при его перемещении в магнитном поле; BdS = dΦ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,

dA = IdΦ.

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Вопрос 25. Циркуляция и ротор вектора индукции магнитного поля. Теорема Гаусса для магнитного поля.

Вывод выражения для циркуляции вектора В

Д окажем, что: циркуляция вектора магнитной индук-ции по произвольному контуру L равна произведению алгебраической суммы токов, охватываемых контуром, на магнитную постоянную μ₀, т.е.

При этом ток I_i в сумме считается положительным, если его направление связано с направлением обхода контура правилом «правого винта».

В ыражение вида (9) получим исходя из закона Био-Савара для случая прямого тока. Пусть ток I направлен за плоскость рисунка. В каждой точке Р контура L вектор В направлен по касательной к окружности радиуса b, проходящей через эту точку. Заменим в выражении для циркуляции произведение B∙dl на B∙dl_B (здесь dl_B - проекция элемента контура dl на направление В). Из рисунка видно, что dl_B ≈ b∙dα (так как dl, dα - малы); тогда, подставив выражение для магнитного поля

п рямого тока В = получаем B∙dl = B∙dl_B = ∙b∙dα = а последующее

интегрирование по α в пределах [0; 2π] дает выражение для циркуляции

что и требовалось доказать.

Ротор вектора В

Е сли ток I в формуле (9) распределен по объему, где расположен контур L, то его можно представить через плотность тока j как I = (интеграл по поверхности S, ограниченной контуром L). Тогда уравнение (9) принимает вид:

П реобразовав левую часть (10) по теореме Стокса (связь циркуляции вектора В с потоком вектора-rot B, т.е.), получаем равенство: которое должно выполняться при произвольном выборе поверхности S, а это возможно только тогда, когда подынтегральные функции в каждой точке имеют одинаковые значения. Таким образом, получаем: или в проекциях на нормаль

Из (11) видно, что rot B совпадает по направлению с вектором плотности тока j.

Т от факт, что циркуляция В (или rot B), вообще говоря, не равны нулю, означает, что магнитное поле – не потенциально (в отличие от электростатического поля, для которого

Такое векторное поле принято называть вихревым (или соленоидальным) полем.

Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах

Интегральная форма

Поток вектора индукции магнитного поля сквозь любую замкнутую поверхность равен нулю:

Эта теорема является фундаментальным законом для магнитного поля (она выполняется для любых магнитных полей) и выражает собой в постулативной форме тот экспериментальный факт, что линии вектора В не имеют ни начала, ни конца – они замкнуты сами на себе (где-то, вообще говоря, на бесконечности).

Иначе можно трактовать теорему Гаусса для В, как отсутствие в природе «магнитных зарядов» (т.е. зарядов, имеющих значение как электрические заряды).

Число линий В, входящих в объем V, ограниченный замкнутой поверхностью S, равно числу линий В, выходящих из этого объема. Следствием из этого является того, что магнитный поток не зависит от формы поверхности и определяется только ее размером S. Иначе говоря, магнитный поток не зависит от формы поверхности, «натянутой» на контур Г.

Дифференциальная форма

Используя теорему Остроградского-Гаусса (для перехода от интеграла по поверхности к интегралу по объему) и с учетом (11), приходим к дифференциальной форме теоремы Гаусса для В:

Дивергенция вектора индукции магнитного поля всюду равна нулю, т.е. магнитное поле не имеет источников и является вихревым (или соленоидальным) полем.