3.2.3 Частотные показатели качества

Для определения частотных показателей качества требуется построение АФХ разомкнутой системы и АЧХ замкнутой системы.

По АФХ определяются запасы:  - по амплитуде,  - по фазе.

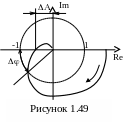Запас  определяется по точке пересечения АФХ с отрицательной действительной полуосью (см. рисунок 1.49).

Для определения  строится окружность единичного радиуса с центром в начале координат. Запас  определяется по точке пересечения с этой окружностью.

По АЧХ замкнутой системы определяются показатели колебательности по заданию М и ошибке М_Е как максимумы соответственно АЧХ по заданию и АЧХ по ошибке.

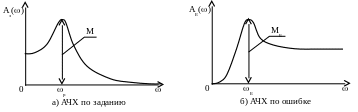
Рисунок 1.50

Для построения АЧХ по заданию необходимо определить передаточную функцию замкнутой системы по заданию Ф_з(s), сделать подстановку s = j^. и построить по ней АЧХ (см. рисунок 1.50, а). Построение АЧХ по ошибке аналогично, но соответственно берется передаточная функция по ошибке Ф_Е(s) (см. рисунок 1.50, б).

Значениям максимумов АЧХ соответствуют резонансные частоты _р (для АЧХ по заданию) и _Е (для АЧХ по ошибке).

К показателям колебательности, а также к запасу по амплитуде предъявляются требования минимальности. Запас по фазе, наоборот, должен быть максимально большим.

3.2.4. Интегральные показатели качества

Интегральные показатели качества определяются путем интегрирования (суммирования) некоторых функций (переходных процессов или других показателей качества). Разновидностью интегральных показателей качества является интегральный квадратичный критерий I₀.

Если рассмотреть два переходных процесса в некоторой АСР (см. рисунок 1.51), то визуально можно определить, что первый процесс обладает более высоким качеством.

Численно это можно охарактеризовать площадью между соответствующей кривой и прямой y = y_уст. Для первой кривой эта площадь (площадь S₁) меньше, чем для второй (площадь S₂), поэтому первый процесс лучше.

Данная площадь определяется как интеграл

и может быть использована как интегральный показатель качества.

Если учесть, что для АСР установившееся значение у_уст должно в идеале совпадать с заданным х, а выражение х – у(t) есть выражение ошибки регулирования e(t), то поиск S сводится к интегралу ошибки. Если в системе имеется статическая ошибка е_ст = х – у_уст  0, то площадь S получается бесконечной. Для учета этого фактора интегрируется не сама ошибка, а ее переходная составляющая

,

где е_п(t) = e(t) – e_уст – переходная составляющая ошибки.

Чаще используется интегральный квадратичный критерий

,

поскольку переходная составляющая на определенных интервалах времени может принимать отрицательные значения, а следовательно, вычитаться из интегральной величины, что приводит к неверному значению площади.

3.2.5 Связи между показателями качества

Описанные выше показатели качества связаны между собой примерными соотношениями, справедливыми только для систем не выше второго порядка:

; t_p = ; ; M = .

4. Настройка регуляторов

4.1. Типовые законы регулирования

Для регулирования объектами управления, как правило, используют типовые регуляторы, которые можно разделить на аналоговые и дискретные. К дискретным регуляторам относятся импульсные, релейные и цифровые. Аналоговые реализуют типовые законы регулирования, названия которых соответствуют названиям типовых звеньев.

Входным сигналом для аналоговых регуляторов является величина ошибки регулирования, которая определяется как разность между заданным и текущим значениями регулируемого параметра (e = х – у). Выходным сигналом является величина управляющего воздействия u, подаваемая на объект управления. Преобразование входного сигнала в выходной производится согласно типовым законам регулирования, рассматриваемым ниже.

1) П-закон (пропорциональное регулирование). Согласно закон пропорционального регулирования управляющее воздействие должно быть пропорционально величине ошибки. Например, если регулируемый параметр начинает отклоняться от заданного значения, то воздействие на объект следует увеличивать в соответствующую сторону. Коэффициент пропорциональности часто обозначают как K₁:

u = K₁^.e.

Тогда передаточная функция П-регулятора имеет вид

W_П(s) = K₁.

Если величина ошибки стала равна, например, единице, то управляющее воздействие станет равным K₁ (см. рисунок 1.52).

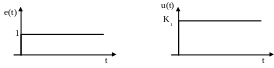
Рисунок 1.52

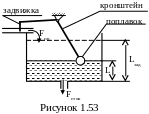Примером системы с П-регулятором может служить система автоматического наполнения емкости (сливной бачок). На рисунке 1.53 обозначены:

L и L_зад – текущий уровень в емкости (регулируемая величина) и его заданная величина,

F_пр и F_сток – расходы жидкости притекающей и стекающей из емкости.

Управляющим воздействием является F_пр. F_сток – возмущение.

Принцип действия понятен из рисунка: при опустошении емкости поплавок через кронштейн открывает задвижку подачи жидкости. Причем, чем больше разница уровней е = L_зад – L, тем ниже поплавок, тем больше открыта задвижка и, соответственно, больше поток жидкости F_пр. По мере наполнения емкости ошибка уменьшается до нуля и, соответственно, уменьшается F_пр до полного прекращения подачи. То есть F_пр = K₁^.( L_зад – L).

Достоинство данного принципа регулирования в быстродействии. Недостаток – в наличии статической ошибки в системе. Например, если жидкость вытекает из емкости постоянно, то уровень всегда будет меньше заданного.

2) И-закон (интегральное регулирование). Управляющее воздействие пропорционально интегралу от ошибки. То есть чем дольше существует отклонение регулируемого параметра от заданного значения, тем больше управляющее воздействие:

.

Передаточная функция И-регулятора:

W_И(s) = .

При возникновении ошибки управляющее воздействие начинает увеличиваться со скоростью, пропорциональной величине ошибки. Например, при е = 1 скорость будет равна K₀ (см. рисунок 1.54).

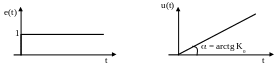
Рисунок 1.54

Достоинство данного принципа регулирования в отсутствии статической ошибки, т.е. при возникновении ошибки регулятор будет увеличивать управляющее воздействие, пока не добьется заданного значения регулируемой величины. Недостаток – в низком быстродействии.

3) Д-закон (дифференциальное регулирование). Регулирование ведется по величине скорости изменения регулируемой величины:

.

То есть при быстром отклонении регулирующей величины управляющее воздействие по модулю будет больше. При медленном – меньше. Передаточная функция Д-регулятора:

W_Д(s) = K₂ s.

Регулятор генерирует управляющее воздействие только при изменении регулируемой величины. Например, если ошибка имеет вид ступенчатого сигнала е = 1, то на выходе такого регулятора будет наблюдаться один импульс (-функция). В этом заключается его недостаток, который обусловил отсутствие практического использования такого регулятора в чистом виде.

На практике типовые П-, И- и Д-законы регулирования редко используются в чистом виде. Чаще они комбинируются и реализуются в виде ПИ-регуляторов, ПД-регуляторов, ПИД-регуляторов и др.

ПИ-регулятор (пропорционально-интегральный регулятор) представляет собой два параллельно работающих регулятора: П- и И-регуляторы (см. рисунок 1.55). Данное соединение сочетает в себе достоинства обоих регуляторов: быстродействие и отсутствие статической ошибки.

ПИ-закон регулирования описывается уравнением

и передаточной функцией

W_ПИ(s) = K₁ + .

То есть регулятор имеет два независимых параметра (настройки): K₀ – коэффициент интегральной части и K₁ – коэффициент пропорциональной.

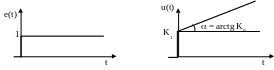При возникновении ошибки е = 1 управляющее воздействие изменяется как показано на рисунке 1.56.

Рисунок 1.56

ПД-регулятор (пропорционально-дифференциальный регулятор) включает в себя П- и Д-регуляторы (см. рисунок 1.57). Данный закон регулирования описывается уравнением

и передаточной функцией:

W_ПД(s) = K₁ + K₂ s.

Данный регулятор обладает самым большим быстродействием, но также и статической ошибкой. Реакция регулятора на единичное ступенчатое изменение ошибки показана на рисунке 1.58.

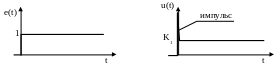
Рисунок 1.58

ПИД-регулятор (пропорционально-интегрально-дифференциальный регулятор) можно представить как соединение трех параллельно работающих регуляторов (см. рисунок 1.59). Закон ПИД-регулирования описывается уравнением:

и передаточной функцией

W_ПИД(s) = K₁ + + K₂ s.

ПИД-регулятор в отличие от других имеет три настройки: K₀, K₁ и K₂.

ПИД-регулятор используется достаточно часто, поскольку он сочетает в себе достоинства всех трех типовых регуляторов. Реакция регулятора на единичное ступенчатое изменение ошибки показана на рисунке 1.60.

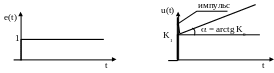
Рисунок 1.60