46.Парная корреляция. Установление тесноты связей. Коэффициент корреляции.

Выборочный коэффициент корреляции r, как всякая выборочная характеристика, является случайной величиной, и по отдельным его значениям нельзя делать окончательные выводы о степени тесноты линейной связи между двумя величинами. Речь может идти о некото­рых практических, качественных рекомендациях (табл. 9.2) при доста­точно больших п (п > 40).

Таблица 9.2. Качественные характеристики связи

Значение г	Характер связи
От 0 до |+ 0,3| От |+ 0,3] до |± 0,5| От |+0,5| до |+0,7| От |± 0,7| до |± 1|	Практически отсутствует Слабая Умеренная Сильная

47.Понятие о методах регрессионного анализа.

После того как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена сте­пень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий ре­зультативный показатель у и аргументы х₁, х₂,..., х_k, отбирают наибо­лее информативные аргументы, вычисляют оценки неизвестных зна­чений параметров уравнения связи и анализируют свойства получен­ного уравнения.

Функция ƭ (х1,х2, ...,хк), описывающая зависимость среднего значе­ния результативного признака у от заданных значений аргументов, на­зывается функцией (уравнением) регрессии. Термин «регрессия» (лат. regression — отступление, возврат к чему-либо) введен английским пси­хологом и антропологом Ф. Гальтоном и связан исключительно со спе­цификой одного из первых конкретных примеров, в котором это поня­тие было использовано. Обрабатывая статистические данные в связи с анализом наследственности роста, Ф. Гальтон нашел, что если отцы отклоняются от среднего роста всех отцов на х дюймов, то их сыновья отклоняются от среднего роста всех сыновей меньше, чем на х дюймов. Выявленная тенденция была названа регрессией к среднему состоянию. С тех пор термин «регрессия» широко используется в статистической литературе, хотя во многих случаях он недостаточно точно характери­зует понятие статистической зависимости.

Для точного описания уравнения регрессии необходимо знать за­кон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии ƭх), так как исследователь не располагает точным знанием условного зако­на распределения вероятностей анализируемого результатирующего показателя у при заданных значениях аргумента х.

Рассмотрим взаимоотношение между истинной регрессией ƭ(х) = М(у/х), модельной регрессией у и оценкой у регрессии Пусть результативный показатель у связан с аргументом х соотно­шением:

у = 2x^1,5 + ɛ,

где ɛ — случайная величина, имеющая нормальный закон распределе­ния, причем Mɛ = O и De = σ². Истинная функция регрессии в этом слу­чае имеет вид:

f(x) = M(y/x)= 2х^1,5.

Предположим, что точный вид истинного уравнения регрессии нам не известен, но мы располагаем девятью наблюдениями над дву­мерной случайной величиной, связанной соотношением у, =2x1,5 + ɛ, и представленной на рис. 9.2.

60-

50-

40-

30-

20-

10-

0-1 1 1 1 т 1 »-

0 2 4 6 8 10 х

Взаимное расположение истинной fix) и теоретической у модели регрессии

Расположение точек на рис. 9.2 позволяет ограничиться классом линейных зависимостей вида: у = Р0 + р,х. С помощью метода, наи­меньших квадратов найдем оценку уравнения регрессии у = b0+btx-Для сравнения на рис. 9.2 приводятся графики истинной функции рег­рессии f{x) ~ 2х1,5, теоретической аппроксимирующей функции рег­рессии у = ро + р,х.

Поскольку мы ошиблись в выборе класса функции регрессии, а это достаточно часто встречается в практике статистических исследова­ний, то наши статистические выводы и оценки окажутся ошибочными.

С целью наилучшего восстановления по исходным статистическим данным условного значения результативного показателя у(х) и неиз­вестной функции регрессии f(x) = M (y/x) наиболее часто используют различные критерии адекватности (функции потерь).

48.Прогноз социально-экономических явлений. Методы прогнозирования.

Необходимым условием регулирования рыночных отношений является составление надежных прогнозов развития социально-экономических явлений. Базу для прогнозирования, т.е. для определения ориентировочных размеров явлений в будущем, создает выявление и характеристика основной тенденции развития социально-экономических явлений во времени.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровней явления во времени, свободное от случайных колебаний.

На практике для того чтобы построить количественную модель, выражающую общую тенденцию изменения уровней динамического ряда во времени, используют аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:

, (1)

где – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней производится на основе адекватной математической модели, которая наилучшим образом аппроксимирует (отображает) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть обоснован в теоретическом анализе, выявляющем характер развития явления, а также в графическом изображении эмпирических (фактических) уровней ряда динамики (линейной диаграмме).

Простейшей моделью, выражающей тенденцию развития явления, является уравнение прямой линии:

, (2)

где а - свободный член; b - коэффициент приращения;t - период времени.

Выравнивание по уравнению прямой линии используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

Расчет параметров функции обычно производится методом наименьших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между эмпирическими и теоретическими уровнями:

. (4)

Параметры а и b согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений, полученной путем алгебраического преобразования условий (4):

(5)

, (6)

где Yi – фактические (эмпирические) уровни ряда;

n – число членов ряда;

t – время (порядковый номер периода или момента времени).

Расчет параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю ( ). При этом используют следующие формулы:

если ряд содержит нечетное число членов

, (8)

если ряд содержит четное число членов

, (9)

где k – порядковый номер года;

n – число лет в периоде.

При условии, что , система нормальных уравнений преобразуется следующим образом:∑t=o

(10)

, (11)

откуда:

(12)

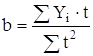. (13)

По рассчитанным параметрам записывают уравнение прямой линии для ряда динамики, представляющей собой трендовую модель искомой функции.

Подставляя в данное уравнение последовательно рассчитанные значения t, находят выровненные уровни .

Если расчеты выполнены правильно, то сумма значений эмпирического ряда должна совпадать с суммой вычисленных уровней выровненного ряда, т.е. .

Затем выровненные значения уровней ряда динамики наносят на поле графика в виде линейной диаграммы.

Для определения прогнозных значений уровней ряда динамики на будущее используют метод экстраполяции.

Под экстраполяцией понимают нахождение уровней за пределами изучаемого ряда, т.е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). Поскольку в действительности тенденция развития остается неизменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки.

На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками, определяя так называемые доверительные интервалы прогноза.

Для определения границ интервалов используют формулу:

, (14)

где - точечная (дискретная) оценка прогнозного значения уровня ряда динамики в момент времени t, стоящего за пределами исследованного ряда динамики;

- остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n-m):

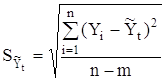, (15)

n - число уровней ряда динамики;

m – число параметров модели тренда (для уравнения прямой m=2);

- коэффициент доверия по распределению Стьюдента при уровне значимости a.

Зная точечную оценку прогнозируемого явления, определяют вероятностные границы интервала прогнозируемого явления:

. (16)

49.Ряды динамики как основной источник прогнозирования социально-экономических явлений.

Прогнозирование — это оценка будущего на основе глубокого анализа тенденций развития социально-экономических явлений и их взаимосвязей. Процесс прогнозирования предполагает выявление возможных альтернатив развития в перспективе для обоснованного их выбора и принятия оптимального решения.

Прогнозирование ведется на основе использования широкого спектра информации. Но первоначальный этап прогнозирования в экономике всегда связан с анализом временных рядов, который позволяет охарактеризовать закономерность изменения явления во времени. Примером временного ряда может служить табл. 8.1

Как видим, в 1990—1998 гг. в России численность занятого населения систематически снижалась и лишь в 1999 г. наблюдался рост.

Временной ряд называется также рядом динамики и представляет собой ряд последовательно расположенных во времени числовых значений соответствующего показателя. Он состоит из двух элементов:

1. периода времени, за который или по состоянию на который приводятся числовые значения;

2. числовых значений того или иного показателя, называемых уровнями ряда.

В нашем примере численность занятого населения - это уровни ряда, обозначаемые обычно через у, а период времени, к которому они относятся, — годы, обозначаемые обычно через t.

По характеру отображения динамики временные ряды делятся на моментные и интервальные. Уровни моментных рядов динамики характеризуют объекты изучения по состоянию на определенный момент времени: численность населения на конец года (или на дату переписи), численность работников предприятия на начало каждого месяца, товарные запасы на складе на начало каждого дня и т.д. Уровни интервальных рядов динамики характеризуют явления за определенный промежуток, интервал времени: товарооборот магазина за квартал, прибыль предприятия за год, выпуск продукции за месяц и т.п. В рас­смотренном выше примере численность занятого населения дана в среднем за год, поэтому ряд, представленный в табл. 8.1, — интервальный.