закономерности в периодах и амплитудах циклов. Из рис. 9.6 также следует, что метод «срезки» достаточно точно позволяет выделить процессы наименьшего и среднего масштабов, что выражается в эф- фективном определении периодов циклов и несколько с

также довольно точно установлен период в 220 (фактический 200) и амплитуда цикла, равная 2 (и фак- тически 2). В результате на

метода ста- тистических испытаний, когда случайным образом

процессов разных масштабов: (9.44)

• продолжительность временного ряда (n).

До проведения моделирования на синтетических примерах были установлены следующие закономерности:

322

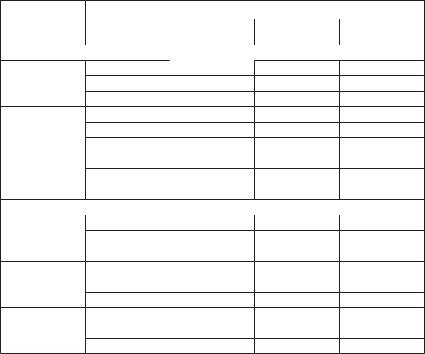
не различаются, или амплитуда процесса А больше, чем процесса В. В этих условиях даже при малом периоде процесса А, что со- ответствуют реальным условиям в гидрометеорологии, можно по- лучить погрешность определения периодов циклов не более 16 %. Еще с меньшей погрешностью определяются периоды циклов для процесса В и для тех же условий составляют не более 6–7 %.

Таблица 9.1

Амплитуды циклов определяются с погрешностью примерно в 2–3 раза большей, чем периоды. При этом, чем больше различие в амплитудах, тем более надежно для процесса соответствующего масштаба они определяются. Так, AB/AA ≤ 1 погрешность определе-

ния амплитуд процесса А варьирует от 30 до 70 %, а при AB/AA > 1

превышает 100 %. Для процесса В точность определения амплитуд повышается при AB/AA > 2 и при уменьшении отношения средних

периодов двух процессов, составляя в этих случаях 20–30 %.

324

и исследованию, например мезомасштабные процессы. Поэтому погрешность процесса может быть получена и непосредственно из анализа временного ряда [7, 8].

В качестве примера таких методов определения погрешности рассмотрим метод единичных пульсаций (МЕП) и метод сглажива- ния экстремумов (МСЭ). В основу предлагаемых методов положены следующие допущения: а) к погрешностям можно отнести «единич- ные» циклы колебаний, имеющие продолжительность 2 единицы дискретности, так как погрешность

Yi 1 Yi 2 , Yi 1 Yi 2 .

Условия (9.45)–(9.46) характеризуют наличие единичной пуль- сации на ветви подъема процесса, условия (9.47)–(9.48) – на фазе спада и условия (9.49)–(9.50) идентифицируют единичную пульса- цию соответственно в области экстремальных значений процесса наименьшего масштаба (рис. 9.7).

Положительные и отрицательные погрешности в МСЭ

где Yi – значение экстремума единичной пульсации.

Отличие метода сглаживания экстремумов состоит в том, что в нем рассматриваются только экстремумы на максимуме и мини- муме цикла, которые затем сглаживаются по формулам (9.51) или (9.52), как показано на рис. 9.7.

326

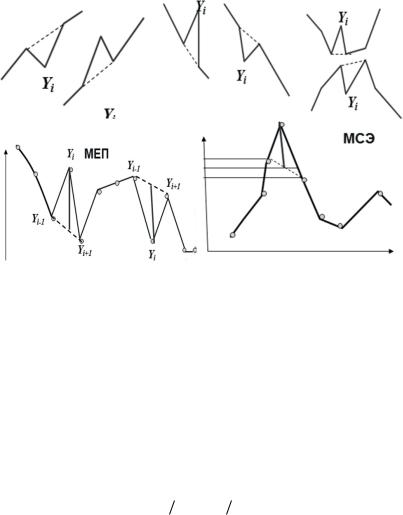
Рис. 9.7. Графическое представление неравенств (9.45)–(9.50) и сравнение МЕП и МСЭ

Оценку эффективности МЕП и МСЭ можно получить аналити- чески из условия, что среднее изменение процесса за единицу дис- кретности ∆t не превышает стандарта погрешности σε, поскольку

в этом случае практически все выявленные экстремумы будет ха- рактеризовать погрешность. Если обозначить дискретность в до- лях среднего периода процесса наименьшего масштаба T, то есть ∆t = K∆tT, а стандарт погрешности – в долях средней амплитуды ци-

клов процесса наименьшего природного масштаба A как σε = KσεA, то изменение функции цикла процесса за один интервал дискрет- ности будет ∆Y = K∆tA. При таких обозначениях

граничное условие применимости методов можно выразить как:

Величина Θ характеризует, во сколько раз средняя изменчи- вость функции цикла процесса за ∆t больше погрешности изме- рений. При Θ = 0 функция неизменна на интервале дискретности, поэтому амплитуды всех определенных экстремумов будут харак- теризовать погрешность измерений. При Θ > 1 изменение функции будет превышать стандарт погрешности и в МЕП такие единичные пульсации практически не могут быть выявлены, а в МСЭ разности

327

между экстремумами и ближайшими значениями в большей степе- ни будут соответствовать изменению процесса, чем величинам по- грешностей.

Условие наиболее эффективной области применения методов имеет место при Θ = 0. Можно принять, что это условие

принять, что дисперсии случайных величин однород- ны, и выразить их через одну дисперсию, что в

выражениях для стандарта позволит получить:

1, 225 Y .

(9.55)

Выражение (9.55) свидетельствует, что методы имеют система- тическую смещенность, равную ∆ = 22,5 %, так как стандарт, опре-

деляемый по (9.51)–(9.52), должен иметь такую же погрешность,

K 1 100 1 . (9.56) что и другие значения, которые в предельном случае отсутствия Полученная теоретически величина смещенности методов в процесса также являются погрешностями. Для учета смещенности 22,5 %, что соответствует корректировочному коэффициенту K = методов был введен корректировочный коэффициент K, на который 0,816, определена для предельного случая – генеральной сово- необходимо умножать полученное значение погрешности по МЕП купности. Для определения зависимости величин смещения, или

или МСЭ, определяемый по формуле корректировочных коэффициентов от объема выборки было прове-

дено статистическое моделирование. Результаты полученных вы- борочных величин смещения (в %) для МЕП (∆') и МСЭ (∆"), так же как и соответствующих корректировочных коэффициентов (K' и K"), приведены в табл. 9.2. Из таблицы видно, что при выборке в 5000 членов выборочное значение смещенности методов практи- чески равно предельному теоретическому.

После тарировки методов была оценена их эффективность для условий, близких к реальным, то есть для композиционных процес- сов, и частоте измерений, не намного меньшей среднего периода ци- клов процесса наименьшего масштаба. При этом процесс задавался

328

суммой гармонических функций от 1 до 5 с разными периодами, амплитудами и начальными фазами. Дискретность измерений (∆t) задавалась в долях наименьшего периода гармоники T1 для восьми

вариантов ∆t = 0,01T1; 0,05T1; 0,1T1; 0,2T1; 0,3T1; 0,4T1; 0,5T1 и 0,6T1. Величина погрешности σε назначалась в зависимости от амплиту-

ды A1 гармоники процесса наименьшего масштаба с периодом T1 как: σε = 0,01A1; 0,05A1; 0,1A1; 0,2A1, 1,0A1; 2,0A1. Закон распреде-

ления погрешностей принимался нормальным с параметрами µ = 0 и σ = σε. Определение погрешностей осуществлялось двумя мето- дами МЕП и МСЭ путем сравнения выборочных и заданных «гене- ральных» значений. Эффективность при этом оценивалась по сле- дующей шкале:

–метод эффективен, если относительная случайная погреш- ность определения дисперсии погрешностей измерений (σε‘) не пре- вышает 10 %;

–метод принимался хорошим при 15 % < σε' < 30 %;

–метод считался удовлетворительным при 30 % < σε'< 50 %;

–метод неудовлетворителен при σε' > 50 %.

В результате получено, что при малой величине погрешности, когда стандартное отклонение составляет 1 % от амплитуды A1,

МЕП и МСЭ позволяют надежно определить дисперсию погреш- ностей независимо от степени сложности процесса только при вы- сокой частоте измерений ∆t = 0,01T1, так как при меньшей частоте

измерений погрешности практически невозможно выявить предла- гаемыми методами. При дальнейшем росте погрешностей может быть увеличена и дискретность измерений ∆t, но ее величина даже при довольно большой погрешности (20 % от A1) не должна пре-

вышать 0,1T1. В качестве предельных случаев рассматривались си-

туации, когда погрешность соизмерима или превышает амплитуду процесса наименьшего масштаба, то есть σε = 1A1 и 2A1. В таких

ситуациях дискретность может быть очень большой, например два- три измерения за период циклов. Интересно отметить, что степень

329

композиционности процесса, то есть число гармоник, оказывает су- щественно меньшее влияние на эффективность методов, чем дис- кретность измерений или сама абсолютная величина погрешностей. Особенность МЕП состоит в меньшем количестве выявляемых по- грешностей, а в некоторых случаях, особенно при дискретности 0,1T1 – 0,4T1 – в отсутствии единичных пульсаций

для анализируе- мой выборки. В целом результаты статистического моделирования подтверждают, что область эффективного применения обоих мето- дов соответствует установленному ранее условию Θ ≤ 1.

Для практической оценки эффективности полученных погреш- ностей можно ввести какой-либо измеряемый показатель, например число единичных пульсаций в исходном ряду, так как,

где η – относительное число единичных пульсаций; me – общее чис- ло единичных пульсаций; N – объем ряда.

Литература

1.Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. – М.: Наука, 1976.

2.Айвазян С.А. Статистическое исследование зависимостей. – М.: Металлургия, 1968. – 227 с.

3.Алексеев Г.А. Методы оценки случайных погрешностей гидрометеоинформа- ции. – Л.: Гидрометеоиздат, 1975. – 96 с.

4.Алимов Ю.И. Элементы теории эксперимента; Измерение моментов случайных величин, векторов и процессов. – Свердловск: Изд. УПИ, 1976. – 104 с.

5.Алимов Ю.И. Элементы теории эксперимента; Измерение распределений веро- ятностей. – Свердловск: Изд. УПИ, 1977. – 80 с.

6.Алимов Ю.И. Элементы теории эксперимента. III часть. Опытная проверка утверждений математической статистики. – Свердловск: Изд. УПИ, 1978. – 91 с.

7.Алимов Ю.И. Измерение моментов системы случайных величин. – Свердловск: изд. УПИ, 1984. – 84 с.

8.Бешелев С.Д., Гуревич Ф.Г. Математико-статистические методы экспертных оценок. – М.: Статистика, 1980. – 263 с.

9.Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. – М.: Наука, 1991. – 379 с.

10.Гренджер К., Хатанака М. Спектральный анализ временных рядов в экономи- ке. – М.: Статистика, 1972. – 312 с.

11.Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и на- уке (методы обработки данных). – М.: Мир, 1980. – 510 с.

12.Дрейпер Н., Смит Г. Прикладной регрессионный анализ. – М.: Статистика, 1973. – 392 с.

330