Кругляк_Прогнозирование_свойств_молекулярных_веществ._Критические свойства фреонов-2018_171_стр_обложки

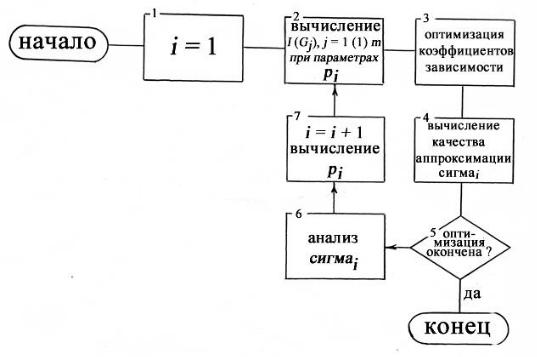
минимума, в то время как другие методы оптимизации, даже самые сложные, такие гарантии не дают. Именно поэтому нами уделялось большое внимание нахождению возможно более жестких ограничений на параметры и соотношений между ними.

Блок-схема апробированного нами алгоритма приведена на рис. 3.

Рис. 3. Общая блок-схема алгоритма оптимизации параметров.

Отметим, что вся предлагаемая нами схема расчета физико-химических свойств как и разработанные нами компьютерные программы являются эффективным инструментом лишь при наличии у исследователя достаточной квалификации. В частности, для параметров, которые входят в инвариант линейно, можно применить множественный регрессионный анализ, если и рассматриваемая функциональная зависимость линейна.

Пусть часть значений параметров уже определена. Оптимизируются параметры, которые входят в инвариант линейно. Например, для двух параметров условие линейности запишется так:

Положим

kp1 k1; kp2 k2; k k3; c k4,

тогда

где S1(i ) , S2(i ) , S3(i ) можно считать значениями независимых переменных при i-ом испытании, а Fi – соответствующее значение зависимой переменной. А эта задача легко решается методами множественного регрессионного анализа, которые всегда есть в арсенале стандартного матобеспечения. По найденным коэффициентам k1, k2, k3, k4 восстанавливаются искомые величины:

Для некоторых классов веществ и инвариантов можно объединить две описанные схемы оптимизации и раздельно оптимизировать линейные и нелинейные параметры молекулярных графов. Блок-схема на рис. 3 на самом деле содержит в себе много различных вариантов оптимизации. Расшифруем возможности, заложенные в каждом блоке.

В блоке 2 по набору параметров pi для каждого соединения (графа) вычисляется заданный (выбранный) ИВГ. Можно вычислять сразу несколько инвариантов, а также можно реализовать схему (3.4), для чего компоненты одного индекса S1 , S2 , S3 можно представить как три самостоятельных индекса.

Блок 3 может представлять собой процедуру восстановления одномерной линейной или нелинейной регрессии, множественного линейного или нелинейного регрессионного анализа, если для одного соединения вычисляется несколько инвариантов или реализуется схема (3.4).

В блоке 4 вычисленные значения свойства сравниваются с экспериментальными значениями. В этом блоке кроме среднеквадратичного отклонения можно вычислять максимальное отклонение, среднюю и максимальную относительную погрешность и т. д. Оценивать качество аппроксимации можно по любой из перечисленных величин или по их линейной комбинации.

Решение о выходе из процедуры или о продолжении счета в блоке 5 зависит от метода оптимизации. Для обычных методов нулевого порядка окончание вычислений происходит при достижении дисперсией σi некоторой заданной величины или по превышению наперед заданного числа итераций.

51

При прямом переборе выход из процедуры означает, что все заданные значения параметров исчерпаны.

Вблоке 6 при оптимизации методом симплекса, например, σi сравнивается

сn предыдущими значениями σj, где n – число параметров. При прямом переборе найденное значение σi сравнивается с хранящимся минимальным значением σmin; если σi < σmin, то σmin полагается равным σi и запоминается соответствующий набор параметров.

Блок 7. В методе симплексов вектор вычисляется по векторам путем сравнения соответствующих σj. В других методах оптимизации может быть другой принцип выбора направления, однако, вся

схема при этом не изменится. При переборе параметров заданный шаг Pk прибавляется к последнему из варьируемых параметров (k – номер параметра). Если значение Pk(i ) достигло своей верхней границы, то Pk(i ) присваивается минимальное значение и предыдущий параметр увеличивается на шаг Pk 1 (вообще говоря, Pk Pk 1 ) и т. д. пока не превысит верхнюю границу первый параметр. Другими словами, реализуется схема некоторой системы счисления, в которой позиция в числе определяет не только масштаб цифры, но и шаг, с которым она изменяется и границы изменения. В нашем программном комплексе [5, 83], написанном на языке PL/1-OS [84] и реализованном на ЭВМ ЕС-1020/1024 [85], была возможность также по значениям k варьируемых параметров определить остальные n–k значений, если при анализе экспериментальных данных найдены некоторые соотношения между этими параметрами.

В написанных нами алгоритмах на каждом шаге итерации вычисляется m значений инвариантов, поэтому успех их применения во многом зависит от скорости вычисления ИВГ. Алгоритмы вычисления разнообразных индексов, основанных на суммировании по конфигурациям смежных ребер, достаточно просты и хорошо известны [86]. Поэтому далее мы остановимся лишь на вычислении нашего нового инварианта паросочетаний.

3.3. Вычисление нового инварианта паросочетаний

Для нахождения чисел P(G, k) (1.11) существуют эффективные алгоритмы. Однако, задача вычисления P(G, k) (2.6) предполагает перебор всех паросочетаний. Представляется целесообразным свести этот процесс к перебору полных подграфов с последовательным увеличением их порядка.

52

Пусть G взвешенный граф с p вершинами и q ребрами, A – вектор размерности p весов вершин, B – вектор размерности q весов ребер. Граф G может задаваться либо бинарной матрицей смежности, либо перечислением пар смежных вершин. В обоих случаях не составляет труда построить матрицу смежности M реберного графа L(G) .

Вершинами графа L(G) являются ребра графа G . Две вершины графа L(G) смежны тогда и только тогда, когда смежны соответствующие им ребра графа G [26].

Поскольку матрица M симметричная, то, сохраняя всю информацию о графе, можно считать ее верхней треугольной, а именно:

Это матрица смежности дополнения графа L(G) . Если L(G) есть дополнение графа L(G) , то любой полный подграф L(G) с k вершинами соответствует набору ребер k-паросочетания графа G .

Все k-паросочетания можно объединить в матрицу

где L P(G, k) , j-ый столбец представляет собой номера ребер, входящих в j-ое k-паросочетание графа G или номера вершин полного подграфа графа L(G) . Таким образом, несложными преобразованиями, легко осуществимыми алгоритмически, задача сводится к перечислению всех полных подграфов графа

L(G) .

53

Это перечисление проводится простым и эффективным способом. При k 1 матрица W1 представляет собой строку номеров вершин: W1 (1, 2,..., q) , а при k 2 матрица W2 – это индексы единиц в матрице M , или номера пар смежных вершин:

Пусть найдена матрица Wk , тогда для вычисления матрицы Wk 1 с каждым

где {lkj } – номера вершин, перечисленных в j-ом столбце матрицы Wk . Когда

где вершины обозначены весами. Связи этого графа задаются таблицей:

54

Составляем матрицы:

Ищем полные подграфы:

Просматриваем последовательно столбцы W2 . Для первого столбца

X X1 X4 (0000011100) ,

Остальные столбцы получаем аналогично:

111111 2222222 33333 W3 444 555 4445554 44555 .

678 678 6786786 78678

Любая конъюнкция для W3 равна нулю. Следовательно, максимальным будет 3-паросочетание. Для него, например, на основе матрицы W3 можно записать:

P(G,3) b1b4b6a2a3a5a7a8 b1b4b7a2a3a5a6a8 ... b3b5b8a1a2a4a6a7.

При программной реализации алгоритма многие действия можно объединить и упростить.

55

56

Глава 4. Прогнозирование критических свойств фреонов

В этой главе приведем наши основные результаты прогнозирования критических свойств фреонов и продемонстрируем процесс их получения. Общая схема подхода к поиску связи «структура – свойство» и к расчету неизвестных свойств (§ 3.1) подробно и поэтапно проиллюстрирована на примере расчета Tc в рядах галогенпроизводных метана, этана и пропана. Нахождение параметров молекулярных графов и коэффициентов регрессионных уравнений для Pc и Vc описано менее подробно. Далее и в Приложении для справочных целей табулированы результаты расчета Tc для всех 35 фреонов метанового ряда, 210 этанового ряда и всех 2100 фреонов пропанового ряда.

4.1. Параметризация и расчет Tc

Для расчета Tc и Pc нами был предложен новый ИП (2.7). Никакие известные нам индексы, модифицированные для взвешенных графов, не выдержали проверки уже на первом этапе анализа неравенств, хотя это не исключает возможности генерации другого индекса, пригодного для решения стоящей перед нами задачи.

4.1.1. Этап 1: Неравенства и ограничения на параметры

Анализ экспериментальных значений в ряду фреонов метанового ряда. На первом этапе сначала выделяем подряды типа

CX4 CX3Y CX2Y2 CXY3 CY4

и ищем ограничения на параметры вершин и ребер при увеличении изучаемого свойства в той же последовательности. Выпишем последовательно для данного подряда выражения для ИП R (2.7) в общем виде:

последовательность неравенств:

4 3a b 2a (a b) 3ba2 a3 4ba3 .

57

Найдем ограничения на параметр b сразу из всех четырех неравенств:

т.е. предположение верно.

58

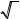
Для сравнения условий (4.5) и (4.6) с (4.2) рассмотрим разность

строгое. Случай 4б не возможен, т.к. из (4.9) следует, что при 4a 3 0 имеет

Такая последовательность возрастания свойства характерна для Tc при:

1)X H,Y Cl; 2)X H,Y Br; 3)X F,Y Cl; 4)X F,Y Br; 5)X Cl,Y Br,

а для Pc при:

1)X F,Y Cl; 2)X F,Y Br; 3)X Cl,Y Br.

Последовательность, отличающаяся от рассмотренной, обнаруживается для Tc при X H,Y F . В этом подряду Tc возрастает в следующем порядке:

CH4, CF4, CHF3, CH3F, CH2F2.

Соответствующие неравенства могут быть удовлетворены при следующих ограничениях на параметры:

В процессе анализа других подрядов по мере расширения числа веществ были найдены еще более строгие неравенства и иные соотношения между параметрами. Здесь же мы демонстрируем лишь анализ неравенств на первом этапе.

4.1.2. Этап 2: Оптимизация параметров

Как уже отмечалось, экспериментальные значения Tc для фреонов, цитируемые в литературе, в большинстве случаев различаются не сильно.

59