2.3.5. Проведение тестовых расчетов в (эт)

Чтобы проверить правильность составления ЭТ, введем в табл. 11. ответы, согласно БД табл.10. Поскольку результат совпадает с тестовыми вычислениями (п. 2.3.1), можно утверждать, что реализация системы принятия решения в ЭТ функционирует нормально.

2.3.6. Подготовка системы принятия решений для пользователя

Разработанная система принятия решения (табл.11 табл.12) содержит много избыточной для пользователя информации. Пользователю совершенно не обязательно знать о наличии базы знаний и о весовых факторах неисправностей, о формулах обработки ответов и принятия решений.

Пользователь должен вводить в ЭТ сведения о своем телевизоре и получать соответствующее решение.

Для исключения лишней информации удобно пользоваться командой "Скрыть строку".

Поставим указатель мыши на номер строки 6 и щелкнем правой клавишей для получения контекстного меню. Выбрать в контекстном меню команду "Скрыть строку". Строка 6 будет скрыта. Проделать эту же операцию со строками 7, 8, 9, 10, 11, 12, 13. Далее скрываем строки 21, 22, 23, 24, 25, 27, 28, 29.

В результате получаем систему принятия решения в режиме пользователя (табл.13).

	A B			C		D
1	СИСТЕМА ПРИНЯТИЯ РЕШЕНИЙ О НЕИСПРАВНОСТИ ТЕЛЕВИЗОРА
2	ВИД НЕИСПРАВНОСТИ
3		ПРЕДОХРА­НИТЕЛЬ	АНТЕННА		КИНЕСКОП
4
14	Вопросы	Ответы
15	Если отвечаете "да "-ввод 1, иначе - ввод 0.
16	Ответы вводить в ячейки В8:В10
17	Отсутствует звук?	1	1		1
18	Отсутствует изображение?	1	1		1
19	Отсутствует световое заполнение экрана?	0	0		0
20	Отсутствует цвет?(ответ в D20)					1
30	ПРИНЯТИЕ РЕШЕНИЯ
31		0	антенна		0

Таблица 13

В этой таблице необходимо еще скорректировать комментарии. В строке 7 следует ввести "Ответы вводить в ячейки В8:В10", а в ячейке А11 -"Отсутствует цвет" (ответ в D11).

2.4 Раcсчет весовых факторов в некоторых системах принятия решений

В рассмотренных ранее системах принятия решений весовые факторы атрибутов для критериев были заданы как постоянные числовые значения. Были рассмотрены различные способы получения результирующего весового фактора для каждого из критериев, необходимого для принятия решения.

В теории принятия решений используются "разумные" процедуры выбора наи­лучшей из нескольких возможных альтернатив. Насколько правильным будет вы­бор, зависит от качества данных, используемых при описании ситуации, в которой принимается решение. С этой точки зрения процесс принятия решений может при­надлежать к одному из трех возможных условий.

1. Принятие решений в условиях определенности, когда данные известны точно.

2. Принятие решений в условиях риска, когда данные можно описать с помо­щью вероятностных распределений.

3. Принятие решений в условиях неопределенности, когда данным нельзя при­писать относительные веса (весовые коэффициенты), которые представляли бы степень их значимости в процессе принятия решений.

В данных методических указаниях мы будем рассматривать примеры и решения задач, относящихся к первым двум случаям.

На практике довольно часто приходится решать задачи, имеющие иерархические уровни с набором критериев и альтернативных решений.

Рассмотрим пример задачи такого вида:

При выборе университета для поступления абитуриент сформулировал два основных критерия для поступления – месторасположение и репутация. Будучи отличным учеником, он оценивает репутацию университета в 5 раз выше, чем месторасположение. Это приводит к тому, что репутации университета приписывается вес примерно 83%, а месторасположению 17%. После проведения системного анализа, суть которого в данном курсе не рассматривается, абитуриент получил следующие альтернативные оценки для трех университетов А, В, С:

Структура задачи принятия решений имеет вид:

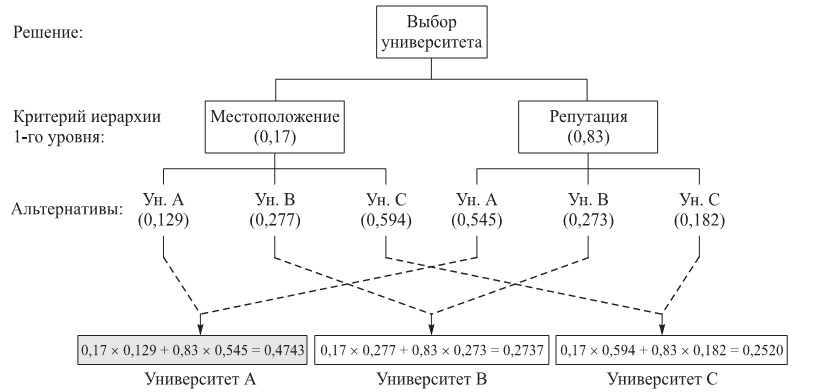
В данной задаче суммарный весовой фактор для принятия решения о поступлении в конкретный университет рассчитывается как сумма произведений базовых и альтернативных весовых факторов атрибутов данного университета.

Оценка трех университетов основана на вычислении комбинированного весового коэффициента для каждого из них.

Университет А: 0,17 х 0,129 + 0,83 х 0,545 = 0,4743.

Университет В: 0,17 х 0,277 + 0,83 х 0,273 = 0,2737.

Университет С: 0,17 х 0,594 + 0,83 х 0,182 = 0,2520.

Очевидно, что для принятия решения необходимо выбрать университет, у которого суммарный весовой фактор наибольший, в данном случае это университет А.

Заметим, что данная задача относится к классу задач на принятие решения в условиях определенности.

Теперь рассмотрим пример и решение задачи на принятие решения в условиях риска.

Предположим, что вы хотите вложить на фондовой бирже 10 000 долл. в акции од­ной из двух компаний: А или В. Акции компании А являются рискованными, но могут принести 50% прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20%. Компания В обеспечивает безопасность инвестиций с 15% прибыли в условиях повышения котировок на бирже и только 5% — в ус­ловиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60% прогнозируют повышение котировок и с вероятностью 40% — понижение котиро­вок. В какую компанию следует вложить деньги?

Информация, связанная с принятием решения, суммирована в следующей таблице.

Эта задача может быть также представлена в виде дерева решений, показанного на рисунке. На этом рисунке используется два типа вершин: квадратик представляет "решающую" вершину, а кружок — "случайную". Таким образом, из вершины 1 ("решающая") выходят две ветви, представляющие альтернативы, связанные с по­купкой акций компании А или В. Далее две ветви, выходящие из "случайных" вершин 2 и 3, соответствуют случаям повышения и понижения котировок на бирже с вероятностями их появления и соответствующими платежами.

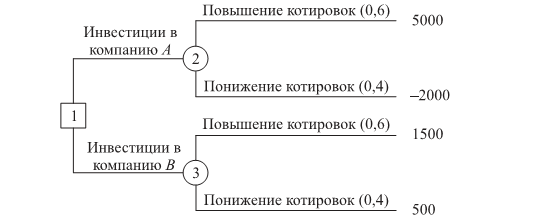
Исходя из схемы рис. 14.4 получаем ожидаемую прибыль за год для каждой из двух альтернатив.

Для акций компании А: 5000*0,6 + (-2000)*0,4 = 2 200 (долл.). Для акций компании B: 1500*0,6 + 500*0,4 = 1 100 (долл.).

Вашим решением, основанным на этих вычислениях, является покупка акций компании А.

В теории принятия решений повышение и понижение котировок на бирже име­нуются состояниями природы, возможные реализации которых являются случай­ными событиями (в данном случае с вероятностями 0,6 и 0,4). В общем случае за­дача принятия решений может включать n состояний природы и m альтернатив. Если p_j — вероятность j-го состояния природы, а a_ij — платеж, связанный с приня­тием решения i при состоянии природы j (i = 1, 2, m, j = 1, 2, n), тогда ожи­даемый платеж для решения i вычисляется в виде

где по определению p₁ + p₂ + … + p_n = 1

Наилучшим решением будет то, которое соответствует

MV_i* = max_i [MV_i} или

MV_i* = min_i {MV_i}, в зависимости от того, является ли платеж в задаче доходом (прибылью) или убытком (затратами).

(прибылью) или убытком (затратами).