§ 9.1. Общие методы

К числу общих методов повышения точности систем автоматического регулирования относятся:

1) увеличение коэффициента усиления разомкнутой цепи;

2) повышение степени астатизма;

3) применение регулирования по производным от ошибки. Увеличение общего коэффициента усиления разомкнутой цепи является

наиболее универсальным и эффективным методом. Увеличить общий коэффи­циент усиления можно обычно за счет введения в систему регулирования усилителей. Однако в некоторых случаях удается достичь этого увеличения за счет повышения коэффициентов передачи отдельных звеньев, например чувствительных элементов, редукторов и т. д.

Увеличение общего коэффициента усиления благоприятно сказывается в смысле уменьшения ошибок практически во всех типовых режимах. Это вытекает, в частности, из того, что общий коэффициент усиления разомкну­той цепи входит в качестве делителя во все коэффициенты ошибок (см. при­мер, рассмотренный в § 8.3).

Однако увеличение общего коэффициента усиления ограничивается устойчивостью системы регулирования. При повышении коэффициента уси­ления, как правило, система приближается к колебательной границе устой­чивости. При некотором предельном его значении в системе возникают неза­тухающие колебания. В этом сказывается противоречие между требованиями к точности и требованиями к устойчивости системы регулирования.

В связи с этим повышение общего коэффициента усиления до значения, нри котором обеспечивается выполнение требований к точности, обычно может производиться только при одновременном повышении запаса устойчи­вости системы, что осуществляется при помощи так называемых корректи­рующих средств, рассматриваемых в следующей главе.

Повышение порядка астатизма. Повышение порядка астатизма исполь­зуется для устранения установившихся ошибок в различных типовых режи­мах: в неподвижном положении, при движении с постоянной скоростью, при движении с постоянным ускорением и т. д. Формально это сводится к тому, чтобы сделать равными нулю первые коэффициенты ошибки системы, например, с₀ = 0 при астатизме первого порядка, или с₀ = с_± = 0 при астатизме второго порядка, или с₀ = с_х = с_% = 0 при астатизме третьего порядка и т. д. Физически повышение порядка астатизма осуществляется за счет введения в канал регулирования интегрирующих звеньев. В качестве таких звеньев могут, например, использоваться звенья, изображенные на рис. 4.21. Структурная схема системы регулирования с введенным интегрирующим звеном изображена на рис. 9.1. Передаточная функция инте­грирующего звена

,

Где k_и [] - коэффициент передачи интегрирующего звена. W (р) представляет собой передаточную функцию разомкнутой системы регулирования до введения интегрирующего звена.

Результирующая передаточная функция разомкнутой системы будет иметь дополнительный множитель р в знаменателе:

Wэ = ,

П

Рис 9.1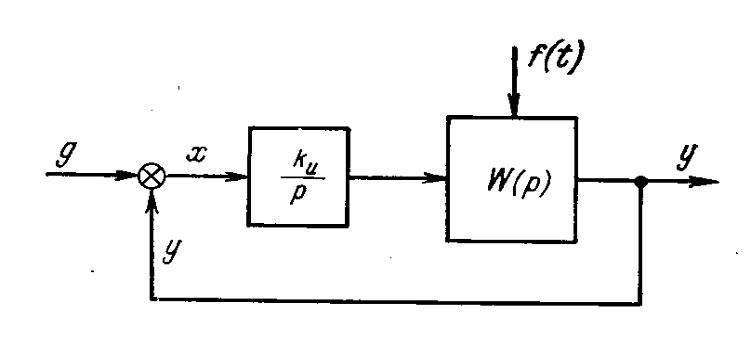

овышение порядка астатизма неблагоприятно сказывается на устойчи­вости системы. Поэтому одновременно с повышением порядка астатизма в системе автоматического регулирования приходится использовать кор­ректирующие звенья, повышающие запас устойчивости (см. главу 10).В качестве иллюстрирующего примера рассмотрим систему, изо­браженную на рис. 6.4. Для нее была получена передаточная функ­ция разомкнутой системы в

W(p) = ,

которая соответствует астатизму пер­вого порядка.

В соответствии с примером, рассмотренным в § 8.3, первые коэффициен­ты ошибки можно записать следующим образом (если положить Т_У = Т₁, Т_М = Т_2, К = К₀):

C₀ = 0,

C₁ = ,

,

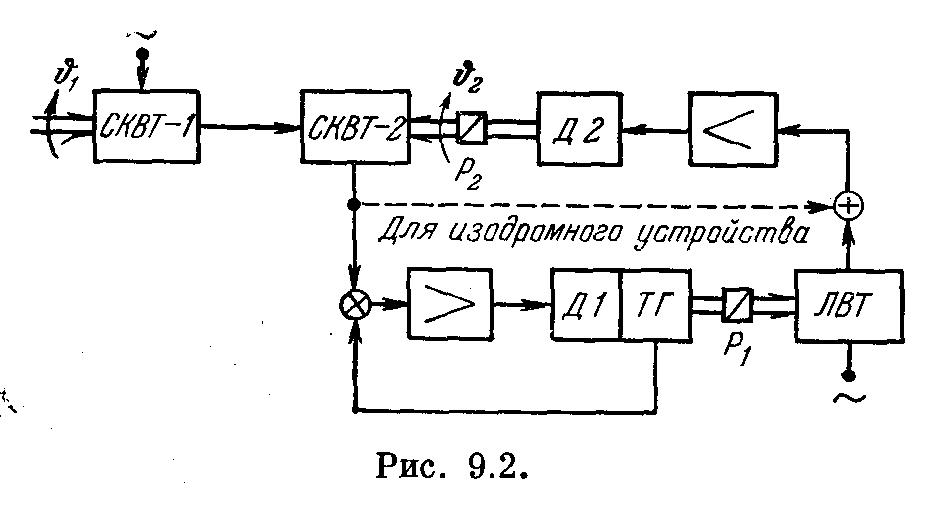
Введем в систему интегрирующее звено, например интегрирующий при­вод. Соответствующая этому случаю электромеханическая схема изображена на рис. 9.2. В этой схеме приняты следующие условные обозначения: СКВТ — синусно-косинусные вращающиеся трансформаторы, ЛВТ — линей­ный вращающийся трансформатор, Д — двигатели, Р — редукторы, ТГ — тахогенератор. Передаточная функция исходной системы без интегрирую­щего звена (9.1) была выведена в § 6.2. Передаточная функция разомкнутой системы, изображенной на рис. 9.2, будет отличаться от (9.1) наличием дополнительного множителя , который дает интегрирующее звено. В результате получим передаточную функцию разомкнутой системы в виде:

W(p) = ,

где К_ε = k_и К [] - добротность системы по ускорению.

Эта передаточная функция соответствует уже астатизму второго порядка. Передаточная функция системы по ошибке

Ф_о = 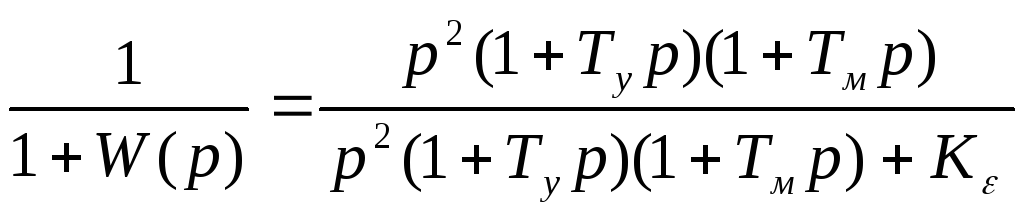(9.4)

Раскладывая эту функцию в ряд делением числителя на знаменатель, полу­чаем вместо (9.2) следующие равенства для коэффициентов ошибок:

C₀ = C₁ = 0, , (9.5)

Сравнивая (9.5) с (9.2), можно заметить, что в результате введения интегрирующего звена вследствие повышения порядка астатизма получено условие с_г = 0, и, следовательно, будет равна нулю

скоростная составляющая ошибки.

Однако, если йковерить теперь систему на устойчи­вость, можно убедиться, что система вообще не может ра­ботать, так как получить ус­тойчивую работу нельзя ни при каком зн^ении общего коэффициента усиления К_г.

Это называется структурной неустойчивостью. Действительно, передаточ­ной функции (9.3) соответствует характеристическое уравнение

в котором отсутствует член, содержащий оператор в первой степени. Пропуск одного из членов в характеристическом уравнении всегда соответствует неустойчивости в соответствии с § 6.1.

Появление неустойчивости в рассматриваемой системе при повышении порядка астатизма можно проиллюстрировать на логарифмических характе­ристиках. Логарифмические характеристики для передаточной функции (9.1) построены на рис. 9.3 по выражениям:

Логарифмические характеристики для передаточной функции (9.3) по­строены на рис. 9.3 по выражениям:

Сравнение рис. 9.3, а и 9.3, б, а также формул (9.7) и (9.9) показывает, что введение интегрирующего элемента дает дополнительный фазовый сдвиг {—90°), в результате чего в рассматриваемой схеме нельзя добиться устой­чивой работы ни при каком значении общего коэффициента усиления. Однако это не означает, что схема явля­ется вообще неработоспособной. Введение в нее корректирующих средств (см. главу 10) позволяет не только достичь устойчивости, но и обеспечить определенный за­пас устойчивости, т. е. выполнить требования к качеству процесса регулирования.

Применение изодромных уст­ройств. Существует путь повыше­ния порядка астатизма системы регулирования без заметного или недо­пустимого ухудшения ее запаса устойчивости. Этот путь заключается в при­менении изодромных устройств, например таких, как изображенные на рис. 4.22. Структурная схема системы регулирования при введении изо­дромного устройства изображена на рис. 9.4. Передаточная функция изо­дромного устройства может быть представлена в виде

Где, постоянная времени изодромного устройства.

Пример введения изодромного устройства показан на рис. 9.5. На рис. 9.5, а изображен чувствительный элемент регулятора давления.

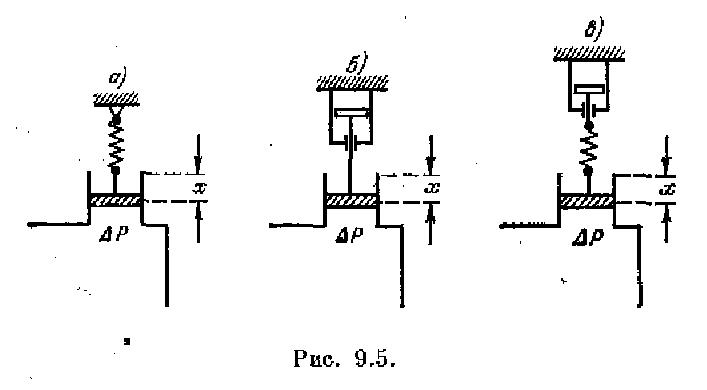
с противодействующей пружиной. Если не учитывать массу движущихся частей, то перемещение чувствительного элемента будет пропорциональным отклонению давления от заданного значения:

Где, к₁ - коэффициент пропорциональности, определяемый жесткостью пружины.

На рис. 9.5, б изображен тот же элемент, но с противодействующим демпфером. Так как сила, развиваемая демпфером, пропорциональна скоро­сти перемещения его поршня, то в этом случае будет иметь место соотношение рх =к₂.∆P Вместо (5.11) получим

где к₂ — коэффициент, определяемый скоростным сопротивлением демпфера. Равенство (9.12) соответствует введению интеграла в закон регулиро­вания.

Наконец, в случае, изображенном на рис. 9.5, в, перемещение чувстви­тельного элемента будет складываться из деформации пружины и перемеще­ния поршня демпфера:

Т_И — постоянная времени изодромного устройства. В качестве второго примера рассмотрим приведениую выше схему следя­щей системы (рис. 9.2). Переход от ведения дополнительного интеграла к ведению изодромного устройства может быть сделан добавлением связи, показанной пунктиром. Передаточная Функция разомкнутой системы может быть получена умножением (9.1)

На передаточную функцию изодромного устройства.

В результате для рассматриваемой схемы получим:

Где, Кε = к_{и *} - добротность системы по ускорению.

Коэффициенты ошибки определяются равенствами:

С₀ = С₁ = 0, ,

Рассматривая характеристическое уравнение системы:

можно убедиться, что в системе возможно получение устойчивости при выполнении условия:

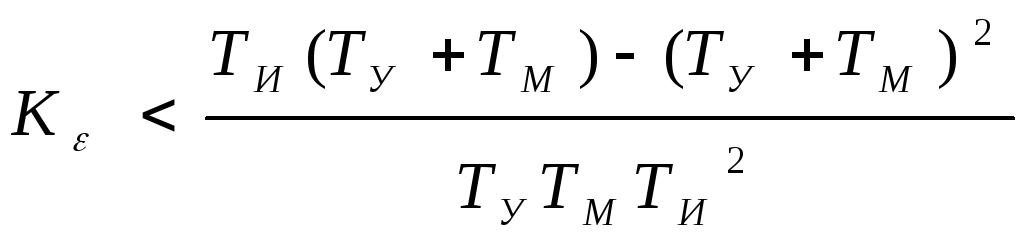
Или в ином виде:

Нетрудно видеть, что при Т_И, стремящемся к бесконечности (это будет при отсутствии интегри­рующего привода в изодромном механизме) условие устойчивости переходит в неравенство

которое справедливо для исходной схемы_т изображенной на рис. 6.4. При достаточно больших значениях постоянной времени изодромного механизма Т_И , что соответствует малому передаточному коэффициенту интегрирующего привода , условия устойчивости (9.16) и (9,7) будут мало отличаться от условия устойчивости (9,18) исходной схемы. Таким об­разом, введение изодромного ме­ханизма с относительно большой постоянной времени Т_И дает повы­шение порядка астатизма на еди­ницу при возможности практиче­ски сохранить условия устойчиво­сти в системе, куда этот механизм вводится. Это обстоятельство можно про­иллюстрировать также на лога­рифмических частотных характеристиках (рис. 9,6). В соответствии с вы­ражением для передаточной функции разомкнутой системы (9.14) можно записать:

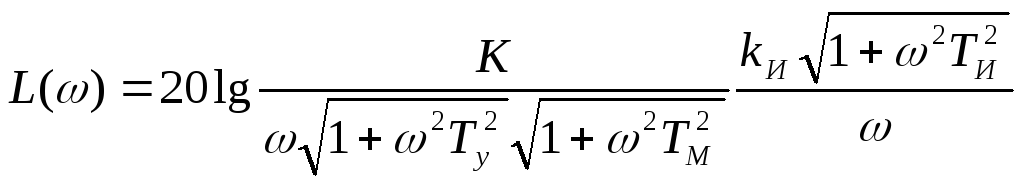
Сравнивая эти выражения с формулами (9.6) и (9,7) справедливыми дл» исходной схемы, можно заметить, что при относительно большом значе­нии постоянной времени Т_ж логарифмические характеристики системы с изодромным устройством будут иметь отличие только в низкочастотной области при . Для частот — дополнительный множитель

в (9.19) обращается в единицу, а дополнительный фазовый сдвиг в (9.20) равен нулю. Таким образом, при -логарифмические частотные характеристики; системы с изодромным устройством практически не отличаются от логарифмических характеристик исходной схемы. В частности, в районе нуля децибел для л. а. х. можно получить одинаковый вид амплитудной и фазовой характеристик для обеих схем, что будет соответствовать одина­ковому запасу устойчивости.

На рис. 9.6 сплошными линиями показаны л. a. x_t и л, ф. х. для исход­ной схемы_т а пунктирными — изменения, даваемые введением изодромного-устройетва с относительно большой постоянной времени.

Следует заметить, что введение изодромного устройства с большой постоянной времени образует систему, динамические качества которой могут оказаться сравнительно низкими. Это объясняется тем, что введение такого устройства улучшает вид амплитудной характеристики только в низкочастот­ной области (рис, 9.6). В результате коэффициенты ошибки, следующие за тем коэффициентом, который обращается в нуль, могут не только не умень­шиться, ио даже возрасти,

В рассмотренном выше примере при введении изодромного устройства обратился в нуль коэффициент c_t (9.15), Однако в следующие коэффициенты

в качестве делителя входит добротность по ускорению . При большом значении постоянной времени Т_И добротность системы по ускорению К_Е получается малой и коэффициенты ошибок с₃, с_а, ... сильно возрастают.

Для дальнейшего повышения порядка астатизма системы регулирова­ния могут применяться не один а два, три и т. д. изодромных устройства. В этом случае можно получить повышение порядка астатизма на один, два, три и т, д. в зависимости от необходимости. На рис. 9.7 в качестве примера приведена структурная схема системы с тремя изодромными устройствами, т. е. схема с тройным изодромированием. Если исходная система имеет,

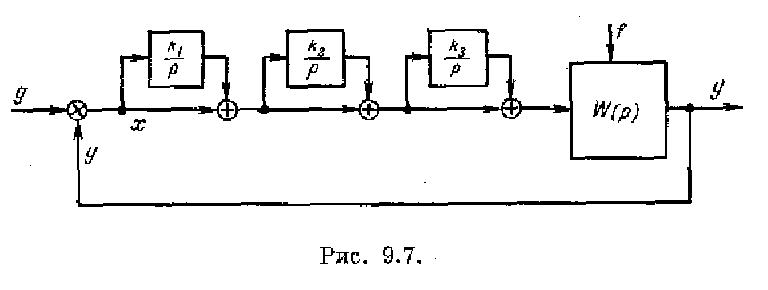
например, астатизм первого порядка, го система рис. 9.7 с изодромными устройствами будет обладать астатизмом четвертого порядка. В этом слу­чае для коэффициентов ошибок будет иметь место равенство с_а = c_f — с₂ = — c_s = 0. Как и ранее, при соответствующем выборе постоянных времени , , можно сохранить практически те же условия устойчивости, что и в исходной системе. Регулирование по производным от ошибки. В большинстве случаев регулирование по производным от ошибки имеет целью повысить запас

устойчивости системы, что позво­ляет увеличить общий коэффициент усиления системы и тем самым улучшить точность регулирования. Это будет рассмотрено более по­дробно в главе 10.

Однако регулирование по про­изводным от ошибки может само­стоятельно повышать точность сис­темы регулирования даже в том случае_т когда сохраняется неиз­менным общий коэффициент усиления в системе. Физика этого явле­ния заключается том, что при введении регулирования по производ­ным система начинает чувствовать не только наличие ошибки, но и тенденцию к изменению ее величины. В результате система регулирования более бистро реагирует на появление задающих и возмущающих воздействий, что сни­жает ошибку регулирования.

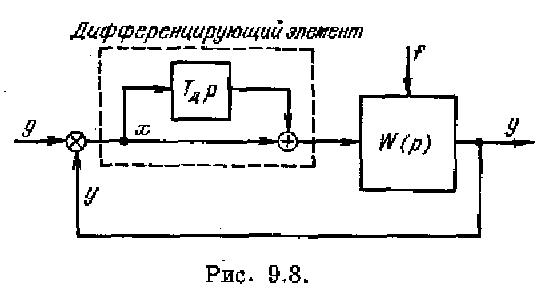
Структурная схема введения производной по ошибке изображена на рис. 9.8. Передаточная функция части прямого канала вместе с включенным дифференцирующим элементом может быть представлена приближенно (в предположении, что дифференцирующий элемент является идеальным) в виде

где Г_д — постоянная времени дифференцирующей цепи. В качестве дифференцирующих элементов могут, например, применяться устройства, изображенные на рис, 4.23 и 4.24.

Рассмотрим в качестве примера ту же систему (рис. 6.4). При введении производной от ошибки при помощи тахогенераторов, уста­новленных на командной и исполнительной осях ,электромеханическая схема.

будет иметь вид, изображенный на рис. 9.9. Здесь приняты следующие обозначения: СКВТ — синусно-косинусные вращающиеся трансформаторы, ТГ — тахогенераторы, Д — двигатель, Р — редуктор. Передаточная функция разомкнутой системы может быть получена умножением (9.1) на передаточную функцию (9,21). В результате получим

где постоянная времени Т_ц представляет собой отношение передаточного

коэффициента тахогенератора к передаточному коэффициенту чувствительного элемента (СКВТ), т. е.

.

Для передаточной функции разомкнутой системы (9.22) находим пере­даточную функцию по ошибке:

Ф_о =

Раскладывая ее в ряд, получаем соотношения для коэффициентов ошибок:

C₀ = 0,

C₁ = ,

,

Сравнивая последние выражения с (9.2), можно заметить, что коэффи­циенты с₄ и с_в (а так же следующие коэффициенты) уменьшаются при введе­нии регулирования по первой производной от ошибки. При соответствующем выборе величины постоянной времени Т_я можно добиться условий с_а = О или с₃ — 0. При с₂ — 0 система не будет иметь установившейся ошибки» пропорциональной ускорению.

Аналогичным: образом, применяя два включенных последовательно дифференцирующих элемента, можно получить равенство нулю одновре­менно двух коэффициентов, например с_а = 0 и с₃ — 0. В этом случае можно показать, что в системе, наряду с регулированием по первой производной от ошибки, будет использоваться регулирование по второй производной. Это вытекает из того_, что передаточная функция двух дифференцирующих элементов, включенных ,'друг за другом в соответствии с рис, 9,8, будет равна произведению двух передаточных функций типа (9,21):

9.25

Где τ_± = Т_Д1 + Т_Д2 представляет собой отношение коэффициентов передачи по первой производной и по ошибке, а - отношение коэффициентов передачи по второй производной и по ошибке.

Как видно из рассмотренного, в отличие от случая введения изодромного устройства (см. рис, 9,4), когда обращается в нуль первый, ранее отличный от нуля коэффициент ошибки, введение дифференцирующего элемента (рис. 9.8) не влияет на этот коэффициент ошибки, но зато уменьшает после­дующие коэффициенты. В связи с этим наиболее эффективное снижение ошибки системы регулирования может быть достигнуто при одновременном использовании изодромных устройств и дифференцирующих элементов.

Так как дифференцирование эквивалентно дополнительному усилению верхних частот, то использование более чем двух дифференцирующих эле­ментов оказывается затруднительным вследствие возрастания влияния высо­кочастотных помех. Число же изодромных устройств ограничивается только получающимся усложнением системы регулирования. Однако и оно обычно не превышает грех.