18.Реляционная алгебра. Теоретико-множественные операции
Реляционная алгебра — формальная система манипулирования отношениями в реляционной модели данных.
Особенности Т-М операций:
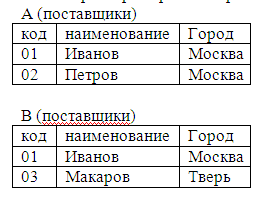
При выполнении Т-М операций должна соблюдаться совместимость отношений по типу: отношения совместимы, если:
-
в их заголовках содержится один и тот же набор имен атрибутов.
-
Одноименные атрибуты должны быть определены на одних доменах.
Если два отношения почти совместимы (количество атрибутов одинаково, отличаются только именами некоторых атрибутов), то они приводятся к полностью совместимым путем операций переименования.
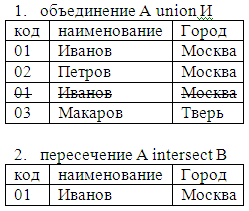
Рассмотрим пример всех переименований:
Прямое произведение:
В РА используют расширенный вариант прямого произведения. Требования к отношениям для этой операции: имена атрибутов не пересекаются.
Свойства Т-М операций (к операциям объединения и пересечения):
-
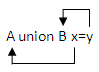
Ассоциативность (A union B) union C = A union (B union C)
-
Переместимость A union B = B union A
19.Реляционная алгебра. Специальные реляционные операции
Реляционная алгебра — формальная система манипулирования отношениями в реляционной модели данных.
Специальные операции:\
-
Выборка – тэта выборка (θ), где θ – одна из простых операций: >, >=, <, <=, =, <>.
Результатом операций выборки является новое отношение, содержащее кортежи исходного отношения, удовлетворяющее условиям: а) x θ y, б) x θ const.
-
Проекция – применяется к исходному отношению, где из него выбирается заданный набор атрибутов.
-
Соединение – имеет 2 варианта: общее и естественное. θ – условие .
Отношения имеют общие атрибуты (заголовки разные)
A times B < θ УСЛОВИЕ >
Частным случаем общей операции является естественное соединение, в котором атрибуты сравниваются по операции «=»
